ПРОГРАММИРОВАНИЕ В MatLab. ОСНОВНЫЕ АЛГОРИТМЫОБРАБОТКИ МАССИВОВ И МАТРИЦ
Цель работы: ознакомиться с возможностями М-языка для обработки массивов и матриц.
Обработка массивов и матриц средствами М-языка
Особенностью программирования задач обработки массивов (одномерных, двумерных) на М-языке является как возможность поэлементной обработки (как в любом языке программирования), так и использования операций MatLab для работы с массивами и матрицами.
Ввод-вывод массивов и матриц
Ввод массивов и матриц следует организовывать поэлементно, на рис. 1 приведена блок-схема алгоритма ввода элементов массивов, а на рис. 2 – матриц.
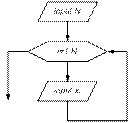
| N=input('N='); for i=1:N х(i)=input(strcat('х(',int2str(i),’)=’)); end |
| Рис. 1Блок-схема «ввод элементов массива» | |

| N=input('N='); M=input('M='); for i=1:N for j=1:M a(i,j)=input(strcat('a(',int2str(i),‘,’,int2str(j),’)=’)); end end |
| Рис. 2Блок-схема «ввод элементов матрицы» |
Для вывода приглашений вида x(i) = и a(i,j) = в функции input использовались функции работы со строками: strcat (s1, s2,..., sn) и int2str(d).
Функция strcat предназначена для объединения строк s1,s2,….,sn в одну строку, которая и возвращается в качестве результата.
Функция int2str преобразует число d в строку символов.
Вычисление суммы и произведения элементов массива (матрицы)
Алгоритм нахождения суммы:
1. До цикла сумма равна 0 (s=0).
2. К s добавляем первый элемент массива и результат записываем опять в переменную s.
3. К переменной s добавляем второй элемент массива и результат записываем в s.
4. Добавляем к s остальные элементы массива.
При нахождении суммы элементов матрицы последовательно суммируем элементы всех строк.
Алгоритм нахождения произведения:
1. Начальное значение произведения равно 1 (р=1).
2. Последовательно умножаем р на очередной элемент и результат записываем в р.
Поиск максимального (минимального) элемента массива (матрицы)
Алгоритм решения задачи поиска максимума и его номера в массиве:
1. В переменной с именем Мах хранится значение максимального элемента массива, а в переменной с именем Nmax – его номер.
2. Предположим, что первый элемент массива является максимальным, и запишем его в переменную Мах, а в Nmax – его номер (то есть 1).
3. Все элементы, начиная со второго, сравниваем в цикле с максимальным.
4. Если текущий элемент массива оказывается больше максимального, то записываем его в переменную Мах, а в переменную Nmax – текущее значение индекса i.
Алгоритм поиска минимального элемента в массиве будет отличаться от приведенного выше лишь тем, что в условном блоке и соответственно, в конструкции if текста программы знак поменяется с > на <.
Алгоритм поиска минимального элемента матрицы и его индексов:
1. Nmin – номер строки, Lmin – номер столбца минимального элемента.
2. При поиске минимального (максимального) элемента матрицы циклы по i и j начинаются с 1. Иначе при обработке элементов будет пропущена первая строка или первый столбец во время сравнения аi,j с min.

| Min=a(1,1); Nmin=1; Lmin=1; for i=1:N for j=1:M if a(i,j) < Min Min=a(i,j); Nmin=i; Lmin=j; end; end; end; |
| Рис. 3Поиск минимального элемента матрицы и его индексов |