Момент инерции тел правильной геометрической формы
Момент инерции материальной точки и абсолютно твёрдого тела

| Определение. Произведение массы i -той точки 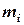 на квадрат расстояния ( на квадрат расстояния ( ) от точки до оси называют моментом инерции материальной точки ) от точки до оси называют моментом инерции материальной точки 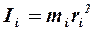 .
Момент инерции АТТ (тело рассматриваем как систему МТ) относительно оси равен сумме моментов инерции точек, составляющих АТТ .
Момент инерции АТТ (тело рассматриваем как систему МТ) относительно оси равен сумме моментов инерции точек, составляющих АТТ 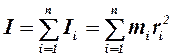 . .
| ||

| Для определения момента инерции тела правильной геометрической формы необходимо мысленно разбить это тело на множество материальных точек  ; найти момент инерции каждой точки ; найти момент инерции каждой точки  , а затем вычислить сумму этих моментов (т.е. проинтегрировать, если масса распределена непрерывно) , а затем вычислить сумму этих моментов (т.е. проинтегрировать, если масса распределена непрерывно)  . .
| ||
2. Момент инерции тонкого стержня длиной l относительно оси, проходящей через его конец перпендикулярно стержню
Пусть масса стержня 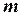 равномерно распределена по его длине с линейной плотностью
равномерно распределена по его длине с линейной плотностью  (равной массе единицы длины).
(равной массе единицы длины).

| Выберем элемент стержня массой dm. Момент инерции этой МТ  , где , где  .
Тогда момент инерции стержня вычисляется .
Тогда момент инерции стержня вычисляется

|
3. Момент инерции тонкого стержня длиной l относительно оси, проходящей через его середину перпендикулярно стержню

|
Рассуждая аналогично п.2, получим

|
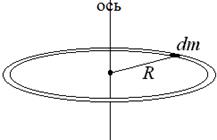
4. Момент инерции тонкого кольца (масса  ) относительно оси, проходящей через его центр перпендикулярно плоскости кольца
) относительно оси, проходящей через его центр перпендикулярно плоскости кольца
Выберем элемент массы кольца  , он находится на расстоянии , он находится на расстоянии  от оси вращения. Момент инерции этого элемента от оси вращения. Момент инерции этого элемента  . После интегрирования по всему кольцу, получим . После интегрирования по всему кольцу, получим
 . .
| 
|
Момент инерции тонкого диска (цилиндра) относительно оси, проходящей через его центр перпендикулярно плоскости диска (по оси цилиндра)
Пусть масса  диска равномерно распределена по его поверхности с поверхностной плотностью
диска равномерно распределена по его поверхности с поверхностной плотностью  (равной массе единицы площади).
(равной массе единицы площади).
Разобьём диск на элементарные кольца массой 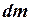 , тогда
, тогда 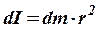 - момент инерции элементарного кольца радиуса r и толщиной dr.
- момент инерции элементарного кольца радиуса r и толщиной dr.

| Масса такого элементарного кольца запишется
 ,
где площадь элементарного кольца вычисляется по формуле ,
где площадь элементарного кольца вычисляется по формуле  . .
|
После интегрирования, получим формулу для вычисления момента инерции диска
 .
.
Заметим, что цилиндр можно представить как совокупность дисков одинакового радиуса R, следовательно, момент инерции цилиндра относительно его оси также выражается формулой  .
.
6. Момент инерции кольца (внутренний радиус  , внешний радиус
, внешний радиус  ) относительно оси, проходящей через его центр перпендикулярно плоскости кольца
) относительно оси, проходящей через его центр перпендикулярно плоскости кольца
Пусть масса  пластинки равномерно распределена по его поверхности с поверхностной плотностью
пластинки равномерно распределена по его поверхности с поверхностной плотностью  (равной массе единицы площади).
(равной массе единицы площади).

|
Разобьём кольцо на элементарные кольца массой  ,
здесь ,
здесь  . .
|
После интегрирования получим
 .
.
Для справки. Без вывода приводим формулу для вычисления момента инерции шара относительно оси, проходящей через его центр,  .
.
7. Момент инерции тонкой однородной прямоугольной пластинки массой  c размерами
c размерами 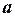 и
и  относительно оси, проходящей через её центр масс и середину стороны
относительно оси, проходящей через её центр масс и середину стороны 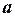
Пусть масса  пластинки равномерно распределена по её поверхности с поверхностной плотностью
пластинки равномерно распределена по её поверхности с поверхностной плотностью  .
.

|
Разобьём пластинку на элементарные пластинки массой  . .
|
После интегрирования получим  .
.
Пропущенные преобразования выполните самостоятельно.
8. Момент инерции тонкой однородной прямоугольной пластинки массой  c размерами
c размерами 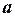 и
и  относительно оси, проходящей через её центр масс и середину стороны
относительно оси, проходящей через её центр масс и середину стороны 
Пусть масса  пластинки равномерно распределена по её поверхности с поверхностной плотностью
пластинки равномерно распределена по её поверхности с поверхностной плотностью  .
.

|
Разобьём пластинку на элементарные пластинки массой  . .
|
После интегрирования получим  .
.
Пропущенные преобразования выполните самостоятельно.
9. Момент инерции тонкой однородной прямоугольной пластинки массой  c размерами
c размерами 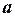 и
и  относительно стороны
относительно стороны 
Пусть масса  пластинки равномерно распределена по её поверхности с поверхностной плотностью
пластинки равномерно распределена по её поверхности с поверхностной плотностью  .
.

|
Разобьём пластинку на элементарные пластинки массой  . .
|
После интегрирования получим  .
.
Пропущенные преобразования выполните самостоятельно.
10. Момент инерции тонкой однородной прямоугольной пластинки массой  c размерами
c размерами 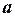 и
и  относительно стороны
относительно стороны 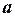
Пусть масса  пластинки равномерно распределена по её поверхности с поверхностной плотностью
пластинки равномерно распределена по её поверхности с поверхностной плотностью 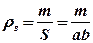 .
.

|
Разобьём пластинку на элементарные пластинки массой  . .
|
После интегрирования получим 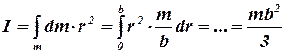 .
.
Пропущенные преобразования выполните самостоятельно.