Таблица изображений некоторых элементарных оригиналов.

| 
| 
| 
|

| 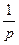
|  
| 
|
 
| 
|  
| 
|
 
| 
|  
| 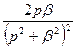
|
 
| 
| 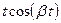 
| 
|
 
| 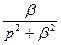
|  
| 
|
 
| 
|  
| 
|
Приведем примеры использования определения и результатов утверждений для нахождения изображений.
 Найти изображение функции
Найти изображение функции  , используя преобразование Лапласа.
, используя преобразование Лапласа.

 Подчеркнем, что
Подчеркнем, что  является оригиналом. Так как
является оригиналом. Так как  для всех
для всех  , то изображение
, то изображение  этой функции будет определено и аналитично в полуплоскости
этой функции будет определено и аналитично в полуплоскости  . Далее находим:
. Далее находим:
 .
.
 Используя таблицу изображений и свойство линейности преобразования Лапласа найти изображения оригинала:
Используя таблицу изображений и свойство линейности преобразования Лапласа найти изображения оригинала: 

 По таблице изображений найдем:
По таблице изображений найдем:  .
.
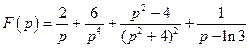 .
.
 Найти изображение функции
Найти изображение функции  , воспользовавшись свойством дифференцирования изображений.
, воспользовавшись свойством дифференцирования изображений.

 Воспользовавшись таблицей изображений, запишем:
Воспользовавшись таблицей изображений, запишем:
 .
.
Тогда по теореме о дифференцировании получим:
 .
.
Последовательно вычисляя производные, находим:
 и далее
и далее  .
.
Окончательно запишем:  .
.
 Найти изображение функции
Найти изображение функции  .
.

 Можно, вычислив интеграл, найти изображение по таблице изображений. Однако в данном случае проще воспользоваться теоремой об интегрировании оригинала. Действительно, имеем:
Можно, вычислив интеграл, найти изображение по таблице изображений. Однако в данном случае проще воспользоваться теоремой об интегрировании оригинала. Действительно, имеем:  . Тогда по теореме об интегрировании оригинала имеем право, записать:
. Тогда по теореме об интегрировании оригинала имеем право, записать:
 .
.
Свертка функций. Отыскание оригинала по изображению.
Сверткой функций  будем называть функцию
будем называть функцию  .
.
Отметим, что операция свертывания обладает свойством коммутативности:  , то есть
, то есть  .
.
Утверждение 10 (об умножении изображений, или теорема о свертке). Пусть  ;
;  . Тогда
. Тогда  .
.
Таким образом, изображением свертки двух оригиналов является произведение их изображений.
 Найти свертку функций
Найти свертку функций  и
и  :
:

 Приведем два способа решения этой задачи.
Приведем два способа решения этой задачи.
Первый способ. Воспользуемся таблицей изображений:  и
и  .
.
Воспользовавшись теоремой о свертке, запишем:  .
.
Итак, изображение свертки найдено. Найдем саму свертку. Для этого, как и в предыдущей задаче, с помощью метода неопределенных коэффициентов представим дробь в виде суммы простейших дробей:  . Тогда по таблице изображений запишем:
. Тогда по таблице изображений запишем:  .
.
Второй способ. Вычислим свертку функций, воспользовавшись определением:  .
.
Интегрируем по частям:  . Следовательно,
. Следовательно,  .
.
Теперь по таблице изображений находим изображение свертки: 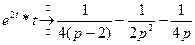 .
.
Итак, нами получен тот же результат.
 Пользуясь теоремой о свертке, найти оригинал изображения:
Пользуясь теоремой о свертке, найти оригинал изображения:  .
.

 Представим изображение
Представим изображение  в виде произведения
в виде произведения  . По теореме о свертке имеем:
. По теореме о свертке имеем:  . Найдем теперь свертку функций
. Найдем теперь свертку функций  и
и  :
:
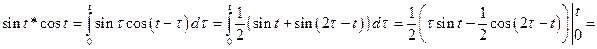
 .
.
Таким образом,  .
.
Заметим, что в данном случае оригинал можно было найти и по таблице изображений.
При нахождении оригиналов по заданным изображениям можно использовать несколько приемов.
Первый состоит в том, что изображение 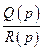 представляется в виде суммы элементарных дробей, каждая из которых является изображением простых оригиналов. Далее, используя таблицу оригиналов и свойство линейности преобразования Лапласа, находят оригинал, соответствующий исходной дроби.
представляется в виде суммы элементарных дробей, каждая из которых является изображением простых оригиналов. Далее, используя таблицу оригиналов и свойство линейности преобразования Лапласа, находят оригинал, соответствующий исходной дроби.
Второй способ состоит в том, чтобы представить дробь в виде произведения дробей, каждая из которых является изображением некоторой функции, и применить теорему о свертке.
Третий способ основан на следующем утверждении:
Утверждение 11 (о разложении). Пусть функция  представляет собой правильную рациональную дробь, имеющую полюсы в точках
представляет собой правильную рациональную дробь, имеющую полюсы в точках  , где
, где  . Тогда оригиналом для неё служит функция
. Тогда оригиналом для неё служит функция  , где сумма берется по всем полюсам.
, где сумма берется по всем полюсам.
Отметим, что данное утверждение допускает некоторое упрощение в случае, когда
а) все корни многочлена, стоящего в знаменателе изображения имеют кратность единица: 

 ,
,
б) корни многочлена, стоящего в знаменателе изображения кратные:


 ,
,  .
.
Приведем примеры использования вышеперечисленных идей при решении задач.
 Найти оригинал изображения:
Найти оригинал изображения:  .
.

 При работе с первым слагаемым по таблице изображений находим:
При работе с первым слагаемым по таблице изображений находим:  . Поэтому, по свойству линейности преобразования Лапласа, находим соответствующий оригинал:
. Поэтому, по свойству линейности преобразования Лапласа, находим соответствующий оригинал:  .
.
Аналогично преобразуем второе слагаемое в выражении:  .
.
Для нахождения оригинала, соответствующего третьему слагаемому 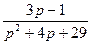 выделим полный квадрат в знаменателе:
выделим полный квадрат в знаменателе:  . С учетом этого запишем:
. С учетом этого запишем:  . Окончательно для этого слагаемого получим:
. Окончательно для этого слагаемого получим:  .
.
Для нахождения оригинала, соответствующего последнему слагаемому  , воспользуемся утверждением запаздывания оригинала. Так как оригинал
, воспользуемся утверждением запаздывания оригинала. Так как оригинал  для функции
для функции  :
:  , то, применив теперь теорему запаздывания оригинала, имеем
, то, применив теперь теорему запаздывания оригинала, имеем 
Итак, оригинал, соответствующий нашему изображению имеет вид:
 .
.
 Найти оригинал изображения:
Найти оригинал изображения:  .
.

 Представим дробь в виде суммы простейших дробей
Представим дробь в виде суммы простейших дробей  .
.
Воспользуемся стандартной техникой нахождения неопределенных коэффициентов  . Приведем правую часть равенства к общему знаменателю. Тогда дроби равны, знаменатели равны, а значит, и числители равны:
. Приведем правую часть равенства к общему знаменателю. Тогда дроби равны, знаменатели равны, а значит, и числители равны:  .
.
Слева и справа у нас многочлены. По теореме о равенстве двух многочленов два многочлена равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях неизвестного. Тогда запишем соответствующую систему и вычислим коэффициенты разложения:
 .
.
Таким образом, исходную дробь представим в виде  .
.
Следовательно,  .
.
Проиллюстрируем теперь использование теоремы о разложении для нахождения оригиналов, соответствующих изображениям.
 Пользуясь теоремой о разложении, найти оригинал изображения:
Пользуясь теоремой о разложении, найти оригинал изображения:  .
.

 Функция
Функция  имеет полюсы второго порядка:
имеет полюсы второго порядка:  ,
, 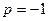 и полюс первого порядка
и полюс первого порядка  . Тогда по тереме о разложении оригиналом для
. Тогда по тереме о разложении оригиналом для  служит функция
служит функция  . Вычислим соответствующие вычеты
. Вычислим соответствующие вычеты  .
.
 ,
,
 ,
,
 .
.
Следовательно, имеем право, записать
 .
.
 Найти оригинал изображения:
Найти оригинал изображения:  .
.

 Заметим, что все корни знаменателя действительные и простые.
Заметим, что все корни знаменателя действительные и простые.
При этом  , а
, а  и
и  .
.
Итак, корни многочлена знаменателя: 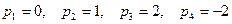 .
.
Найдем соответствующие коэффициенты:  ,
,  ,
,  ,
,  .
.
Следовательно,  .
.
Приведем также пример ситуации с кратными корнями.
 Найти оригинал изображения:
Найти оригинал изображения:  .
.

 Разложение изображения на простые дроби имеет вид:
Разложение изображения на простые дроби имеет вид:  .
.
Найдем коэффициенты этого разложения
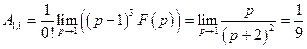 ;
;
 ;
;

 ;
;
 ;
;

??????????
Методы операционного исчисления удобно использовать при решении некоторых дифференциальных и интегро-дифференциальных уравнений, а также систем таких уравнений. При этом предполагают, что в правой части такого уравнения стоит оригинал некоторой функции. Приведем примеры использования утверждений, касающихся свойств оригиналов и изображений.
 Найти частное решение дифференциального уравнения
Найти частное решение дифференциального уравнения
 .
.
 Пусть функция
Пусть функция  , удовлетворяющая данному уравнению имеет изображение:
, удовлетворяющая данному уравнению имеет изображение: 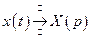 . Тогда воспользовавшись утверждением о дифференцируемости оригинала запишем:
. Тогда воспользовавшись утверждением о дифференцируемости оригинала запишем:
 , а
, а  .
.
Правая часть уравнения преобразуется следующим образом:
 .
.
Приходим к операторному уравнению:  .
.
Выразим из полученного уравнения изображение  частного решения дифференциального уравнения:
частного решения дифференциального уравнения:
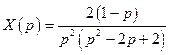 .
.
Найдем разложение получившейся дроби на сумму дробей, представляющих собой оригиналы элементарных функций.
 .
.
Следовательно,  решение исходной задачи Коши.
решение исходной задачи Коши.
 Найти общее решение дифференциального уравнения
Найти общее решение дифференциального уравнения 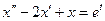 .
.
 Выберем произвольные начальные условия задачи Коши. Пусть
Выберем произвольные начальные условия задачи Коши. Пусть  . И пусть
. И пусть 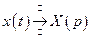 . Тогда
. Тогда
 и
и  , кроме того
, кроме того  . И соответствующее операторное уравнение имеет вид:
. И соответствующее операторное уравнение имеет вид:  .
.
Выразим отсюда  :
:
 .
.
И значит решением исходного уравнения будет функция
 . (здесь
. (здесь  ).
).
 Решить интегральное уравнение
Решить интегральное уравнение  .
.
 Выпишем уравнение для изображений, воспользовавшись утверждением 8 об интегрировании оригинала. (Полагая, что
Выпишем уравнение для изображений, воспользовавшись утверждением 8 об интегрировании оригинала. (Полагая, что  ).
).
 . Выразим функцию изображения
. Выразим функцию изображения  . Найдем оригинал, соответствующий данному изображению
. Найдем оригинал, соответствующий данному изображению  .
.
 Решить интегральное уравнение
Решить интегральное уравнение  .
.
 Отметим, что левая часть уравнения представляет собой свертку функций
Отметим, что левая часть уравнения представляет собой свертку функций 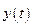 и
и  . Переходя к соответствующим изображениям запишем
. Переходя к соответствующим изображениям запишем
 . Выражая из последнего уравнения
. Выражая из последнего уравнения  убедимся
убедимся  . И, значит, этому изображению соответствует оригинал
. И, значит, этому изображению соответствует оригинал  .
.
 Решить систему уравнений
Решить систему уравнений 
 Пусть
Пусть 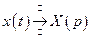 и
и  .Выпишем соответствующую операторную систему линейных уравнений
.Выпишем соответствующую операторную систему линейных уравнений
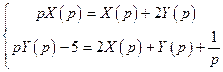 .
.
Выразим из получившейся операторной системы  и
и  :
:
 ,
,  .
.
Отметим, что для нахождения соответствующих оригиналов удобно воспользоваться теоремой разложения, учтя при этом, что корни знаменателя имеют первую кратность.
Таким образом  , и
, и  .
.
 Найти изображение функции Хевисайда:
Найти изображение функции Хевисайда:  (см. рис.)
(см. рис.)


 Ранее было получено, что изображением для оригинала
Ранее было получено, что изображением для оригинала  является функция
является функция 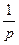 , тогда, воспользовавшись теоремой запаздывания, получим:
, тогда, воспользовавшись теоремой запаздывания, получим: 
 .
.
 Найти изображение функции, заданной следующим графиком:
Найти изображение функции, заданной следующим графиком:


 Аналитически запись этой функции будет выглядеть следующим образом:
Аналитически запись этой функции будет выглядеть следующим образом:

Поэтому ее изображение можно найти, используя формулу преобразования Лапласа, учитывая области определения кусочно-заданного оригинала:

 .
.
 Найти изображение ступенчатой функции, изображенной на рисунке.
Найти изображение ступенчатой функции, изображенной на рисунке.


 Аналитически запись этой функции будет выглядеть следующим образом:
Аналитически запись этой функции будет выглядеть следующим образом:
 . Это легко проверяется графическим сложением функций
. Это легко проверяется графическим сложением функций  ,
,  ,
, 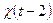 и т.д., изображенных на одном и том же чертеже. По теореме запаздывания получаем:
и т.д., изображенных на одном и том же чертеже. По теореме запаздывания получаем: 

 . Второй сомножитель из правой части равенства представляет собой геометрическую прогрессию, со знаменателем
. Второй сомножитель из правой части равенства представляет собой геометрическую прогрессию, со знаменателем  . Так как,
. Так как,  , то геометрическая прогрессия сходится, и получаем:
, то геометрическая прогрессия сходится, и получаем: 

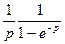 .
.