Решения задач средствами пакета Matlab

Лабораторная работа по теме

«Тема 6.6. Технология решения задач одномерной

Оптимизации средствами математических

Пакетов»

 

Вопросы, подлежащие изучению

Получение таблиц значений функции и ее производных с использованием средств пакетов Mathcad и Matlab.

Технология использования встроенной функции пакета Mathcad – Minimize().

3. Технология использования встроенной функции пакета Matlab – fminbnd()/

Условие унимодальности функции.

Методы одномерной оптимизации: метод дихотомии и метод золотого сечения.

 

Общее задание

Выбрать индивидуальное задание из таблицы 6.6-1.

2. С использованием средств пакетов Mathcad и Matlab:

· построить график функции f1(x), выбрать отрезок, содержащий минимум, и проверить на нем условие унимодальности функции;

· найти минимум f1(x) с использованием встроенных функций.

3. Провести «ручной расчет» 3-х итераций по поиску минимума функции f2(x) на отрезке [a;b], в соответствии с заданным методом.

Варианты индивидуальных заданий

Таблица. 6.6-1.

№	f1(x)	f2(x)	[a;b]	Метод оптимизации
			[0;1]	дихотомия
			[-1; 0]	золотое сечение
			[-0,5;0,5]	дихотомия
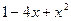
			[0;1]	золотое сечение
			[3;4]	золотое сечение
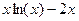
			[2;4]	дихотомия
			[0.5;1.5]	дихотомия
			[1,5;2,5]	золотое сечение
			[-1,5;-0,5]	дихотомия
			[-4;-3]	золотое сечение
			[-1;1]	золотое сечение
			[0;2]	золотое сечение
			[4;6]	дихотомия
			[-1;1]	золотое сечение
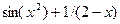
			[0;2]	дихотомия
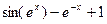
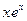
			[-2; 0]	золотое сечение
			[1;3]	золотое сечение
			[0,5;1,5]	дихотомия
			[2;3]	золотое сечение
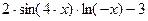
			[4,3;5,3]	дихотомия
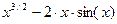
			[-3;-1]	дихотомия
			[-1,5;-0,5]	золотое сечение
			[1;2]	дихотомия
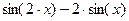
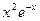
			[-1;1]	золотое сечение
			[0,5;1,5]	дихотомия

 

Содержание отчета

1. Вариант индивидуальное задание:

· f1(x) – для нахождения минимума средствами пакетов Mathcad и Matlab;

· f2(x), [a,b] и метод – для проведения ручного расчета.

2. Результаты исследования индивидуального варианта задания:

· график функции ;

· начальный отрезок неопределенности;

· результаты проверки аналитического условия унимодальности функции на выбранном отрезке.

3. Результаты вычисления координат точки минимума встроенными функциями пакетов Mathcad и Matlab.

4. Результаты «ручного просчета», представленные в табл. 6.6.2, и длина отрезка, содержащего точку минимума, после трех итераций (пример «ручного расчета» приведен в ЛР-1-06).

Таблица 6.6-2

№ итерации	a	b	x1	x2	f(x1)	f(x2)

 

Пример выполнения задания

1. Задан вариант индивидуального задания:

• функция ;
• функции на отрезке [1;2].

Построить график функции f1(x); выбрать отрезок, содержащий минимум, и проверить на нем условие унимодальности функции; найти минимум f1(x) с использованием встроенных функций.

Решения задач средствами пакета Mathcad

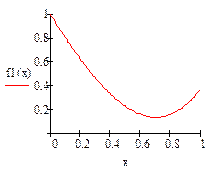
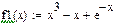
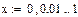
Отделение отрезка унимодальности Первая производная не убывает, а вторая - положительна, следовательно, на отрезке [0;1] существует единственный минимум Вычисление координат точки минимума на отрезке [1;2]   Построим график функции f2(x) на заданном отрезке

 

Решения задач средствами пакета Matlab

function y=ext(x) y=x.^3-x+exp(-x); end   >>x=0:0.2:1; >>f=x.^3-x+exp(-x) % функция >> f1=3*x.^2-exp(-x)-1 % первая производная >> f2=6*x + exp(-x) % вторая производная % Таблица значений функции и производных syms y; >> y=[x;x.^3-x+exp(-x);3*x.^2-exp(-x)-1;6*x + exp(-x)]   y = 0 0.2000 0.4000 0.6000 0.8000 1.0000 1.0000 0.6267 0.3343 0.1648 0.1613 0.3679 -2.0000 -1.6987 -1.1903 -0.4688 0.4707 1.6321 1.0000 2.0187 3.0703 4.1488 5.2493 6.3679   % Первая производная не убывает, а вторая - положительна, % следовательно, на отрезке [0;1] существует единственный минимум   >> x=-2:0.1:2; >> y=ext(x); >> plot(x,y,'-')   %Вычисление координат точки минимума на отрезке [0;1] [x,y]=fminbnd(@ext,0,1); >> x x = 0.7056 >> y y = 0.1395 %Вычисление координат точки минимума функции f2(x) на отрезке [1;2] >> x=1:0.05:2; >> y=2*x.^3-16*x+5; >> plot(x,y,'-') >> [x,y]=fminbnd(@ext,1,2); >> x x = 1.6330 >> y y = -12.4186

 

6.6.6. Контрольные вопросы по теме

«Тема 6.6. Технология решения задач одномерной