ПРАКТИКА № 18 Числовые ряды.
Задача 1. Найти сумму ряда. 
.
Решение. Чтобы разбить на группы слагаемых, часть из которых будет взаимно сокращаться, сначала разложим знаменатель на множители: 
затем надо разбить на простейшие дроби. 
= 
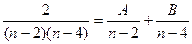, откуда 
, 
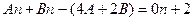, получаем систему 
, отсюда 
.
Тогда ряд можно представить так: = 
= 
Здесь для любого знаменателя, начиная от 3 и выше, всегда есть отрицательная дробь с таким знаменателем, а через 2 шага точно такая же положительная. Таким образом, сокращается всё, кроме 
.
Ответ. 
.
Выяснить сходимость.
Задача 2. Выяснить, сходится или расходится ряд 
.
Решение. По интегральному признаку Коши, можем рассмотреть несобственный интеграл, эквивалентный данному ряду по сходимости. 
= 
= 
= 
= 
.
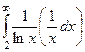Интеграл расходится, значит, и ряд расходится.
Ответ. Расходится.
Задача 3. Выяснить, сходится или расходится ряд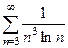 
.
Решение. Заметим, что 
для любого 
. Тогда ряд (по признаку сравнения) можно ограничить сверху другим рядом, <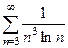 
, который, в свою очередь, сходится, так сходится эквивалентный ему несобственный интеграл 
(заменяем по интегральному признаку Коши). Итак, ответ: ряд сходится (добавим, что сходится абсолютно, так как все слагаемые и так положительны).
Ответ. Сходится.
Задача 4. Выяснить, сходимость ряда 
.
Решение. По признаку сравнения в непредельной форме, 
, таким образом, этот ряд получается больше, чем некоторый расходящийся > 
. Гармонический ряд расходится, это было доказано в лекциях ранее. Поэтому ответ: расходится.
Замечание. Здесь есть и 2-й способ - по интегральному признаку Коши. Ряд эквивалентен интегралу 
= 
=
= .
Ответ. Расходится.
Выяснить сходимость по признаку Даламбера:
Задача 5. Выяснить, сходимость ряда 
.
Решение. Запишем предел отношения последующего (n+1) члена ряда к предыдущему (n). Модули здесь не особо нужны, так как все члены ряда и так положительны, т.е. если сходимость есть, то она заодно и абсолютная.
= 
= 
= 
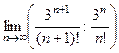=0.
Итак, 
, ряд сходится (абсолютно).
Ответ. Сходится абсолютно.
Задача 6.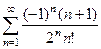 
Решение. Запишем предел отношения модуля (n+1) члена ряда к модулю n-го. При этом мы отбрасываем знакочередование.
= 
= 
=
= 
.
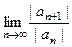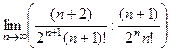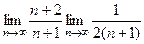Итак, , ряд сходится (абсолютно).
Ответ. Сходится абсолютно.
Задача 7. Выяснить сходимость ряда: 
.
Решение. По признаку Даламбера.
, 
= 
.
Тогда 
= 
=
= 
= 
.
ряд сходится (абсолютно).
Ответ. Сходится абсолютно.
Задача 8. Выяснить сходимость ряда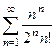 
.
Решение. По признаку Даламбера.
, 
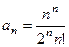Тогда = 
=
= 
= 
= 
= 
, ряд расходится.
Ответ. Расходится.
Задача 9. Выяснить сходимость ряда 
.
Решение. Здесь можно действовать по радикальному признаку Коши.
= 
= 
= 
=
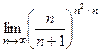используя 2-й замечательный предел, получаем 
. 
, ряд сходится (абсолютно).
Ответ. Сходится абсолютно.
Задача 10. Выяснить сходимость ряда 
.
Решение. По радикальному признаку Коши:
= 
= 
= 
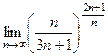. Здесь даже не надо использовать 2-й замеч. предел, так как нет неопределённости: и числитель, и знаменатель стремятся каждый к конечному числу.
= 
= 
< 1, абсолютно сходится.
Так как мы изначально рассматривали модуль, то сходимость абсолютная.
Ответ. Сходится абсолютно.
Задача 11. Выяснить сходимость ряда 
.
Решение. Заметим, что 
, тогда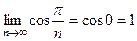 
. Таким образом, 
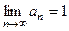, то есть слагаемые не уменьшаются и не стремятся к нулю, тогда по необходимому признаку ряд расходится. Не выполнено необходимое условие сходимости (слагаемые должны уменьшаться к 0 при росте n).
Ответ. Расходится.
Поиск области сходимости функциональных рядов.
Задача 12. Найти область сходимости ряда 
.
Решение. По признаку Даламбера, надо найти отношение модуля следующего слагаемого к модулю предыдущего, причём здесь мы это делаем для произвольного параметра 
.
= 
= 
.
Теперь надо решить неравенство 
. Если 
, то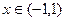 
есть область гарантированной абсолютной сходимости. За пределами этого интервала расходимость. А вот поведение ряда в граничных точках 
и 1 надо исследовать вручную, подставляя каждую точку и получая числовой ряд.
При 
: 
, такой ряд сходится, так как степень 2, больше 1, (про это был факт в лекциях).
При : 
, такой ряд тем более сходится, причём абсолютно, так как по модулю было бы , а этот ряд сходится (только что заметили, на 1 строку выше).
Таким образом, точки и 1 здесь тоже войдут в область сходимости, и ответ: ряд абсолютно сходится в [-1,1].
Ответ. Сходится абсолютно в [-1,1].
Задача 13. Найти область сходимости ряда 
.
Решение. По признаку Коши, 
= 
,
Замечание: есть и 2-й способ: по признаку Даламбера.
= , то есть в итоге всё равно пришли к тому же неравенству.
, что равносильно: 
или 
, т.е. 
. Для граничных точек получаются числовые ряды 
, либо 
,
для которых нет сходимости (по необходимому признаку, т.к. слагаемые не стремятся к 0).
Ответ. Ряд абсолютно сходится в 
.
ПРАКТИКА № 19
Задача 1. Найти область сходимости ряда 
.
Решение. По признаку Даламбера, 
= 
, тогда 
, что равносильно выполнению одновременно двух неравенств: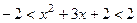 
.
Для правого неравенства, получаем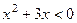 
, корни 
, оно верно для 
.
Для левого неравенства, 
, но это выполняется на всей числовой прямой, т.к. корней нет, а ветви этой параболы направлены вверх. Верно для 
. Пересечением этих двух множеств является интервал 
.
Также легко заметить, что в граничных точках ряд принимает вид
, расходится.
Ответ. абсолютно сходится в .
Задача 2. Найти область сходимости ряда 
.
Решение. По признаку Коши, 
= 
, тогда 
. Из правого неравенства следует 
, т.е. 
.
Из левого неравенства, 
, 
, 
.
Проверяем граничные точки. 
расходится,
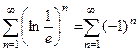, тоже расходится.
Ответ. Ряд абсолютно сходится в интервале 
.
Задача 3. Найти область сходимости ряда 
.
Решение. 
= 
= 
.
В обеих граничных точках получим 
= , расходится.
Ответ. Ряд абсолютно сходится в интервале 
.
Задача 4. Найти область сходимости ряда 
.
Решение. 
= 
.
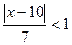
В граничных точках получим и , эти ряды расходятся.
Ответ. Ряд абсолютно сходится в интервале 
.