РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ НЕРАВЕНСТВ.
ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧ
ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Система линейных неравенств имеет вид:
 a11 x1 + a12 x2 +…+ a1n xn < b1
a11 x1 + a12 x2 +…+ a1n xn < b1
a21 x1 + a22 x2 +…+ a2n xn < b2
………………………………
am1 x3 + am2 x2 +…+ amn xn < bm
Кроме знака «<» в записанных неравенствах могут использоваться и другие знаки: «>», « », «
», « ». В случае двух переменных система принимает вид
». В случае двух переменных система принимает вид
 a11 x + a12 y < b1
a11 x + a12 y < b1
a21 x + a22 y < b2
………………...
am1 x + am2 y < bm
Множеством решений системы линейных неравенств с двумя переменными называют множество всех пар чисел (x, y), при подстановке которых в систему все неравенства будут верными.
Системы линейных неравенств достаточно часто используются при построении математических моделей экономических процессов. Обычно такие неравенства ограничивают область изменения определенных параметров, оказывающих влияние на искомый результат. В частности речяы/ь может идти об эффективном использовании некоторого ограниченного запаса ресурсов с целью получения максимальной прибыли или минимизации затрат на производство. Естественно, изменяя в допустимых пределах параметры производства (объем выпуска продукции каждого вида, запасы сырья, трудовые ресурсы и т.п.), можно получить значительное количество вариантов решения, среди которых надо выбрать оптимальный. Методы решения задач на экстремум функции с многими переменными при наличии некоторых ограничений на область изменения этих переменных изучает специальный раздел математики – математическое программирование. Функция, максимум (минимум) которой требуется при этом найти, называется целевой функцией. Если во всех ограничениях и в целевой функции переменные содержался только в первой степени, имеем задачу линейного программирования, при более высоких степенях – задачу нелинейного программирования.
В общем виде задача линейного программирования формулируется следующим образом: найти максимум (минимум) целевой функции
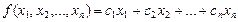
при условиях
 a11 x1 + a12 x2 +…+ a1n xn
a11 x1 + a12 x2 +…+ a1n xn  a10
a10
a21 x1 + a22 x2 +…+ a2n xn  a20
a20
………………………………
ak1 x1 + ak2 x2 +…+ akn xn  ak0
ak0
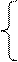 |
a (k+1)1x1 + a(k+1)2 x2 +…+ a(k+1) n xn=a(k+1)0
………………………………………………..
a m1x1 + am2 x2 +…+ am n xn=am0
 x1
x1  0
0
x2  0
0
……..
xp  0(p
0(p 
В симметричной форме задача линейного программирования запишется так: найти максимум (минимум) целевой функции
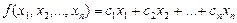
при условиях
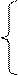 |
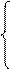 a11 x1 + a12 x2 +…+ a1n xn
a11 x1 + a12 x2 +…+ a1n xn  a10 x1
a10 x1  0
0
a21 x1 + a22 x2 +…+ a2n xn  a20 x2
a20 x2  0
0
……………………………….……
am1 x1 + am2 x2 +…+ amn xn  am0 xn
am0 xn  0
0
Набор чисел (x1, x2,…,x п), удовлетворяющих указанным условиям, называют планом. Среди всех возможных планов может существовать оптимальный план (x1*, x2*,…, x п *), дающий целевой функции максимальное (минимальное) значение.
Для решения задачи линейного программирования с двумя переменными можно использовать графический метод. В этом случае задача принимает вид
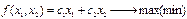
при условиях 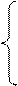
a11 x1 + a12 x2  a10
a10
a21 x1 + a22 x2  a20
a20
………………….
am1 x1 + am2 x2  am0
am0
x1  0, x2
0, x2  0
0
При использовании графического метода в плоскости (x1, x2) строится область допустимых решений задачи, определяемая условиями, и вектор с = (с1, с2), который будет показывать направление наискорейшего возрастания функции f (соответственно вектор - с будет показывать направление наискорейшего убывания). если на плоскости построить семейство параллельных прямых, перпендикулярных к вектору с, то для всех точек каждой из таких прямых f = const. Например, для прямой, перпендикулярной к вектору с и проходящей через начало координат. f = 0 (рис. 14). Искомая точка максимума находится перемещением прямой f = const в направлении вектора с параллельным образом. Максимума функция достигнет в последней точке области допустимых решений, через которую пройдет перемещаемая прямая f = const (на рис. 14 - это точка А). Аналогично перемещением прямой в противоположном направлении находится минимум функции.
|
|

|

Рис. 1. Графический метод решения задачи линейного программирования с двумя переменными.
РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
1. Решите систему линейных неравенств
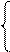 x1 + x2
x1 + x2 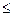 6
6
x1 + 2x2 > 6
x1  0
0
Решение. Покажем вначале на координатой плоскости множество точек, удовлетворяющих первому неравенству. Для этого построим прямую x1 + x2 = 6 по двум точкам:
| X1 | ||
| X2 |
Эта прямая разбивает координатную плоскость на две полуплоскости, одна из которых и будет содержать точки, удовлетворяющие данному неравенству. Для того чтобы определить, какая из двух полуплоскостей содержит точки - решения неравенства, подставим в это неравенство координаты точки 0 (0, 0): 0 + 0 < 6. т.е. оно верно. Следовательно, речь идет о полуплоскости, содержащей точку 0 (0, 0). На рис. 15, а она заштрихована. Поскольку точки, принадлежащие прямой x1 + x2= 6, также являются решением неравенства х1 + х2  6, прямая изображена на рисунке сплошной линией. (Если бы неравенство имело вид x1 + x2<6, то точки прямой не входили бы в множество решений и ее следовало бы изобразить пунктирной линией.) Обычно, чтобы не загромождать рисунок, штрихуют не всю полуплоскость, а только ее небольшую часть, прилегающую к прямой, как это показано на рис. 15, б. Аналогично ищем решения неравенств x1 + 2x2 > 6 и x1
6, прямая изображена на рисунке сплошной линией. (Если бы неравенство имело вид x1 + x2<6, то точки прямой не входили бы в множество решений и ее следовало бы изобразить пунктирной линией.) Обычно, чтобы не загромождать рисунок, штрихуют не всю полуплоскость, а только ее небольшую часть, прилегающую к прямой, как это показано на рис. 15, б. Аналогично ищем решения неравенств x1 + 2x2 > 6 и x1  0, предварительно построив по двум точкам графики соответствующих прямых:
0, предварительно построив по двум точкам графики соответствующих прямых:
| x1 + 2x2 = 6 | И | x1 = 0 | |||
| X1 | X1 | ||||
| X2 | X2 |
|
|
|
|
|
|
|
|
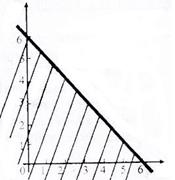

Рис. 2 Множество решений неравенства X1+X2 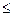 6
6
При этом следует учитывать, что график прямой х1 + 2x2 = 6должен быть изображен пунктирной линией, так как точки данной прямой не являются решениями неравенства х1 + 2x2 > 6 (рис. 16).
|
|
|

Рис. 3
Решениями системы неравенств будут все точки плоскости, в которой пересекаются три штрихованные области. Как следует из рисунка, это будут точки, принадлежащие области АВС. причем точки, лежащие на отрезках АС и АВ, входят в множество решении неравенства, а точки отрезка ВС -нет.
2. Предприятие выпускает продукцию двух видов А и В, для производства которых требуетсясырье трех видов M, N, P, в следующих количествах:
| Вид сырья | Потребности сырья, т. Для производства 1 т. продукции вида | |
| А | В | |
| M | ||
| N | ||
| P |
Запасы сырья М составляют 140 т, N - 150 т, Р - 180 т. Продажа 1 т продукции вида А дает прибыль 2 у.е., продукции вида В – 3у.е. Определите, какое количество продукции вида А и В следует выпускать предприятию для получения максимальной прибыли.
Решение. Обозначим через x1 объем производства продукции вида А, а черезx2 – объем производства продукции вида В. Тогда прибыль от реализации продукции вида А составит 2x1, а от реализации продукции вида В - 3x2. Общая прибыль предприятия в этом случае
f =2x1+3x2àmax
ограничения па затраты сырья запишутся в виде
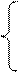 |
x1 + 2x2 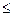 140
140
3x1 + x2 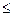 150
150
3x1 + 2x2 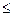 180
180
x1  0, x2
0, x2  0
0
Последние дна неравенства показывают, что количество выпушенной продукции не может быть отрицательным числом.
Для применения графического метода решения задачи па координатной плоскости построим графики прямых
x1 + 2x2 = 140, 3x1 + x2 = 150, 3x1 + 2x2 = 180, x1= 0, x2= 0.
Прямые строим по двум точкам:
| x1 + 2x2 = 140 | 3x1 + x2 = 150 | 3x1 + 2x2 = 180 | ||||||||
| x1 | x1 | x1 | ||||||||
| x2 | x2 | x2 |
Далее по аналогии с предыдущей задачей находим область допустимых решений (рис. 17). Затем строим вектор с = (2, 3) и перпендикулярно к нему линию нулевого уровня. Перемещая полученную линию параллельным образом, находим точку, в которой целевая функция достигает максимума. Этобудет точка В; она является последней точкой области, касающейся перемещаемой линии. Найдем её координаты:
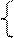 x1 + 2x2 = 140
x1 + 2x2 = 140
3x1 + 2x2 = 180
|
|
|
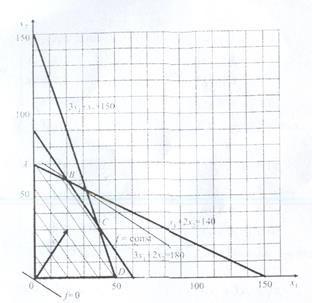
Рис. 4
Решая данную систему, находим координаты точки В: x1=20, x2=60.
Таким образом, максимальная прибыль будет достигнута при плане выпуска продукции вида А 20 т и продукции вида В 60 т. При этом прибыль составит
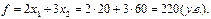
СИМПЛЕКС МЕТОД