Угадай 2/3
ü Три игрока;
ü необходимо назвать 2/3 от среднего, которое назовут игроки.
Очевидно, что среднее арифмитическое не будет больше 100 очков (даже если все игроки скажут – 100, среднее будет – 67), в таком случае каждый из игроков знает, что ни одно число из промежутка 67 и 100 не будет являться средним и не скажет его.
Зная предыдущее, среднее относительно нового максимального значения (т.е. 67), не может быть больше 45. То есть, если все игроки знают, что все знают, что никто не выберет от 67 до 100, то выбирать в промежутке от 45 до 67 также бессмысленно.
Если все игроки сдали на «отлично» теорию игр, то можно сделать вывод, что все игроки придут к тому, что они напишут число 1.
Два политика выбирают программу

Товарищество; партнёрство

Дуополия по Курно
 |


5. Дуополия по Бертрану


Выбор места жительства
Имеются два города (г. Западный и г. Восточный) и 2 типа людей (Умные и красивые). Функция выйгрышей для умных выглядит следующим образом: 
Первые 2 равновесия являются строгими и устойчивыми.
1 равновесие: 100 тысяч человек Умных в г. Западный.
100 тысяч человек Красивых в г. Восточный.
2 равновесие: 100 тысяч человек Умных в г. Восточный.
100 тысяч человек Красивых в г. Западный.
Следующие 2 равновесия являются нестрогими и неустойчивыми.
3 равновесие: В каждом городе по 50 тысяч каждого типа.
4 равновесие: Все едут в один город – произойдет индивидуальный рандом.
Камень, ножницы, бумага
| К | Н | Б | |
| К | 0;0 | 1;-1 | -1;1 |
| Н | -1;1 | 0;0 | 1;-1 |
| Б | 1;-1 | -1;1 | 0;0 |
1/3
1/3
1/3
1/3 1/3 1/3
В чистых стратегиях равновесия Нэша нет.
Теорема. Любая биматричная игра имеет хотя бы одно Равновесие Нэша, которое может быть в области смешанных стратегий.
M[u1(К{1/3;1/3;1/3})]=(1/3)*0+(1/3)*1+(1/3)*(-1)=0
M[u1(Н{1/3;1/3;1/3})]=(1/3)*(-1)+(1/3)*0+(1/3)*1=0
M[u1(Б{1/3;1/3;1/3})]=(1/3)*1+(1/3)*(-1)+(1/3)*0=0
РНСС: {1/3;1/3;1/3}
Теннис
| Серена (S) | ||||
| l | r | |||
| Венус (V) | L | 50;50 | 80;20 | p |
| R | 90;10 | 20;80 | 1-p | |
| q | 1-q |
Попытаемся найти РНЧС. Увидим что их нет.
Будем искать РНСС.
Ищем q (по выигрышам Венус):
Uv (L;q) = 50*q + 80*(1-q) = 80-30*q
Uv (R;q) = 90*q + 20*(1-q) = 70*q+20
Из системы получим, что q=0.6
Ищем p (по выигрышам Серены):
Us (l;p) = 50*p + 10*(1-p) = 40*p+10
Us (r;p) = 20*p + 80*(1-p) = 80-60*p
Из системы получим, что p=0.7
Таким образом РНСС: [(0.7;0.3); (0.6;0.4)]
Проверка:
Uv (L;(0.6;0.4)) = 50*0.6 + 80*0.4 = 62
Uv (R;(0.6;0.4)) = 90*0.6 + 20*0.4 = 62
Uv (p;q) = 0.7*62 + 0.3*62 = 62
То есть строгого желания покинуть РН нет, следовательно РНСС найдено верно.
Однако, существует 2 эффекта игры:
1) Серена натренирует левую руку, => q увеличится
2) Венус узнала, что Серена натренировала левую руку, и теперь лучше подавать вправо => q снизится
Какой из эффектов преобладает можно узнать, исходя из новой матрицы выигрышей:
| Серена (S) | ||||
| l | r | |||
| Венус (V) | L | 30;70 | 80;20 | p |
| R | 90;10 | 20;80 | 1-p | |
| q | 1-q |
РНЧС нет, значит ищем РНСС.
Uv (L;q) = 30*q + 80*(1-q) = 80-50*q
Uv (R;q) = 90*q + 20*(1-q) = 70*q+20
q = 0.5 (по сравнению с предыдушей вероятностью (q=0.6) мы видим что текущая меньше => возобладал эффект 2)
Us (l;p) = 70*p + 10*(1-p) = 60*p+10
Us (r;p) = 20*p + 80*(1-p) = 80-60*p
p = 7/12 = 0.583
РНСС: [(0.583;0.417); (0.5;0.5)]
Налогоплательщик
Игра «Налогоплательщик» - это игра для нахождения РНСС.
 P*=<p*1 ,..., p*n> - РНСС, если
P*=<p*1 ,..., p*n> - РНСС, если
P*i=ЛОi (p-i*)  I
I  N
N
ü 2 игрока (налогоплательщик и аудитор).
ü Стратегии: налогаплательщик (честный/нечестный), аудитор (проверять/не проверять).
Матрица:
| Налогоплательщик | ||||
| Аудитор | Быть честным | Не честным | ||
| Проверять | 2;0 | 4;-10 | P | |
| Не Проверять | 4;0 | 0;4 | 1-p | |
| q | 1-q |
Равновесия Нэша в чистых стратегиях нет.
Найдем РНСС, для этого введем p и q (рандомизации).
| q: UA (П, q) = 2*q+4*(1-q)=4-2q UA (НП) = 4*q 4-2q=4q q=2/3 | p: UН (Ч, p) = 0 UН (НЧ, p) = -10*p+4*(1-p)=-14p+4 -14p+4=0 p=2/7 |
РНСС: ({2/7;5/7};{2/3;1/3})
Если мы изменим один из выигрышей игрока Н, то получится матрица:
| Налогоплательщик | ||||
| Аудитор | Быть честным | Не честным | ||
| Проверять | 2;0 | 4;-20 | P | |
| Не Проверять | 4;0 | 0;4 | 1-p | |
| q | 1-q |
Равновесия Нэша в чистых стратегиях нет.
Найдем РНСС, для этого введем p и q (рандомизации).
| q: UA (П, q) = 2*q+4*(1-q)=4-2q UA (НП) = 4*q 4-2q=4q q=2/3 | p: UН (Ч, p) = 0 UН (НЧ, p) = -20*p+4*(1-p)=-24p+4 -14p+4=0 p=1/6 |
РНСС: ({1/6;5/6};{2/3;1/3})
Результаты:
1. С помощью РНСС можно предсказать пропорции людей, которые будут играть ЧС.
2. Для проверки справедливости РНСС, рассматривается уход игроков в ЧС.
3. Последствия от замены элементов в матрице выигрышей:
Замена элементов в матрице выигрышей у игрока, выигрыши которого стоят по строкам, влияет на распределение вероятностей у игрока, выигрыши которого стоят по столбцам и наоборот.
Деньги в шляпе
Условия:
2 игрока
Стратегии игрока 1: {0;1;3}
Стратегии игрока 2: {1; забрать} и {3;забрать}
Выигрыши 1:
u1=0 => 0
u1=1 => +1, s2=1
u1=3 => +3, s2=3
Выигрыши 2:
s1=1, s2=1 => u2=+1.5
s1=3, s2=3 => u2=+2
s1=0 => u2=0
Игра:
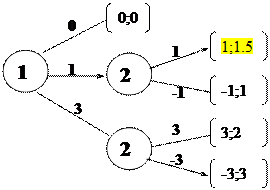
ОИ: (1;1,5), однако (3;2) > (1;1.5) – проблема моральных обязательств
Варианты интерпретации игры в пользу ухода к эффективному решению:
1) Закон о банкротстве
2) Предоставить бизнес-план инвестору
3) Рассрочка платежа банком
4) Поменять выигрыши (вместо (3;2) поставить например (1,9;3))
5) Рентабельность вложения первого игрока (в случае замены выигрышей):
3*1руб. > 1*3руб.
6) Залог
Таким образом, 1 игрок должен так менять выигрыши второго, чтобы максимизировать свой выигрыш: 1-> u2! max u1
Игра «1066»
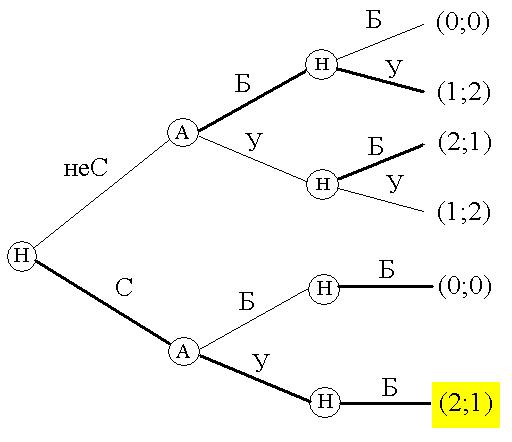
Имеется следующее дерево игры.

Где первая цифра – выйгрыш Норманцев, а вторая – Англичан; Б – вести бой; У – убежать.
Имеются следующие выйгрыши и с помощью метода обратной индукции находим стратегию (У;Б), дающий выйгрыш (1;2) – т.е. 1 – выйгрыш Норманцем, а 2 выйгрыш Англичан.
Но так как Англия – это остров и Норманцы приехали туда на кораблях, то у генерала есть выбор: сжигать или нет все корабли. Если все корабли будут сожжены, то у них нет пути к отступлению. Тогда дерево игры будет следующим.
Таким образом Норманцы сожгут корабли, пойдут в Атаку, а Англичанам выгоднее отступить, так как 1>0.
Дуополия Штакельберга
ü 2 игрока
ü Фирма 1 принимает первой решения, фирма 2 – второй.
ü Фирма 2 знает о решениях, принимаемых фирмой 1 (то есть его стратегия зависит от q1)®
q1 Þ q2 ¯
(q1+ q2) ÞP ¯
p2¯ÞTR1
Возможен излишек производства Сs
Используем метод обратной индукции:
Спрос описывается следующей функцией:

Тогда максимальная прибыль первого игрока можно найти через производную:


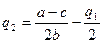
Вторая производная прибыли по q1 равна:
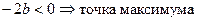
Аналогично для второго игрока, однако в соответствии модели Штакельберга, фирма 2 ориентируется на величину продукции фирмы 1.

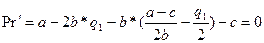
Решая данное уравнение получаем, что:
 - Монопольное производство; а
- Монопольное производство; а 
Фирма 2 может увеличить прибыль, если:
· Снизит предельные издержки
· Обладает большим количеством информации
· Имеет преимущество первого хода
Дуэль двух игроков
ü 2 игрока
ü Игроки продвигаются на встречу друг к другу. После каждого сделанного шага, игрок может выстрелить или нет.
(График – смотрите в тетради)
В этой игре мы следуем 2 фактам:
1. Если никто не выстрелил, то i игрок (в d) знает, что j игрок (в d-1) не выстрелил, то i не стреляет тоже.
2. Если никто не выстрелил, то i игрок знает, что j игрок (d-1) стреляет, то i игрок стреляет Pi(d)>=1-Pj(d-1) (вероятность твоего попадания больше, чем промажет соперник).
Pi(d)+Pj(d-1)>=1
На отрезке от 0- d* используем ОИ, а на отрезке d*-бесконечности доминирование.
1. Рассмотрим, что точки лежат правее d*
d> d*
никто стрелять не будет, так как вероятность попадания каждого из игроков уменьшается.
2. Точки лежать левее d*
d< d*
d=0 P1(d=0)=1 первый стреляет
d=1 P2(d=1) второй стреляет
d=2 P1(d=2) первый стреляет
итд
3. d* - перелом
d=d* оба игрока будут стрелять
Переговоры
Условия:
Есть 1 доллар, 2 игрока. Первый делает предложение какой-либо суммы второму (себе оставляет остаток), если второй принимает – они забирают свои деньги, если не принимает, оба получают по нулям.
Стратегии игрока 1: {1-s1}, Причем s1є[0;1]
Стратегии игрока 2: {принять} и {отклонить}
 |
ОИ: (s1; 1-s1), причем U(1-s1)≠1-s1
Теперь рассмотрим случай, когда игра многошаговая, и второй игрок отклонив предложение может сделать первому свое предложение. Однако примем во внимание принцип дисконтирования. ∆<1 (и предположим что ∆=0,9). То есть второй игрок, отклонив предложение, рассчитывает уже не из 1, а из 0,9 доллара.
Таким образом можем составить таблицу:
| N | 1 игрок |  2 игрок 2 игрок
|
| (точка А) | ||
| (точка Б) | 1-∆ | ∆ |
| 1-∆*(1-∆) = 1-(∆-∆2) | ∆*(1-∆) = ∆-∆2 | |
| 4… | 1-∆*(1-∆*(1-∆)) | ∆*(1-∆*(1-∆)) = ∆-∆2+∆3 |
| 1-∆+∆2-∆3+…+∆8-∆9 | ∆-∆2+…-∆8+∆9 |
Что означает, что на первом шаге игрок 1 может предложить второму любую сумму >=0, но тот, зная что игра двухшаговая, откажет. На втором шаге игрок 2 может забрать себе только сумму <=∆ (но уже не 1), первый примет предложение, причем его выигрыш будет близок к нулю! Таким образом, игрок 1 может сразу предложить второму сумму ∆, а себе оставить 1-∆ (что уже не ноль1), тогда игрок 2 примет предложение.
Если игрок 1 знает, что игра трехшаговая, то максимальная сумма, которой игрок 1 будет распоряжаться на 3-м шаге, это ∆2. Таким образом, игрок 1 должен сразу предложить игроку 2 сумму ∆-∆2, и он согласится. Тогда игрок 1 заберет себе 1-∆-∆2 (что опять же не 0).
Таким образом, в зависимости от количества шагов игры первый игрок будет предлагать второму определенную сумму, учитывая фактор дисконтирования.
Теперь найдем найдем ∆, при котором будет равное распределение выигрышей между игроками.
S10 (u1 в 10м шаге) = 1-∆+∆2-…+∆8-∆9
Домножим обе части на ∆:
∆ S10=∆-∆2+∆3-…+∆9-∆10
Сложим два уравнения системы:
S10+∆ S10=1-∆10
S10=(1-∆10)/(1+∆)
1- S10=(∆-∆10)/(1+∆)
N->∞
SN=(1-∆∞)/(1+∆)=1/(1+∆), где ∆ приблизительно равен 1, SN=1/2
1-SN=∆/(1+∆), где ∆ приблизительно равен 1, SN=1/2
Выводы по игре:
1) Равное распределение при трех условиях: N->∞, ∆->1, ∆ во всех временных периодах постоянна;
2) Первое предложение будет принято, если известно ∆1 и ∆2 И известна функция выигрыша U
3) U может различаться: 1 игрок беднее чем 2й