Тема: «Перпендикуляр и наклонная. Теорема о трёх перпендикулярах »
План
1. Расстояние от точки до плоскости.
2. Расстояние между параллельными плоскостями.
3. Расстояние между прямой и плоскостью.
4. Теорема о трёх перпендикулярах.
5. Угол между прямой и плоскостью.
6. Решение задач.
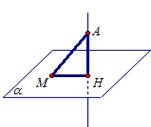 |
Расстояние от точки до плоскости.
Рассмотрим плоскость α и точку А, которая лежит вне
этой плоскости. Как известно, из точки А можно провести
единственную прямую АH перпендикулярную плоскости α.
Проведем прямую АН перпендикулярно плоскости α,  .
.
Определение. Отрезок АН называется перпендикуляром, проведенным из точки А к плоскости α. То есть, перпендикуляр – это отрезок.
Определение. Пусть точка М другая произвольная точка плоскости α. Тогда отрезок АМ называется наклонной, а отрезок МН называется проекцией наклонной АМ на плоскость α.
Определение. Расстоянием от точки А до плоскости α называют длину перпендикуляра АН. Обозначается: ρ(А; α) = АН. Заметим, что АН – наименьшее из расстояний между точкой А и любой точкой плоскости. Действительно, в прямоугольном треугольнике АНМ перпендикуляр (катет АН) короче наклонной (гипотенузы АМ).
Таким образом, чтобы найти расстояние между точкой и плоскостью, нужно найти длину перпендикуляра от точки до плоскости.
Расстояние между параллельными плоскостями.
 Плоскость α и плоскость β параллельны. На плоскости β
Плоскость α и плоскость β параллельны. На плоскости β
выберем произвольную точку А. Из точки А опустим
перпендикуляр АА0 на плоскость α.
Перпендикуляр АА0 - расстоянием между плоскостями α и β.
Заметим, что длина этого перпендикуляра не зависит от того,
какую точку мы выбрали.
Например, выберем другую точку В, опустим перпендикуляр ВВ0. Прямые АА0 и ВВ0 перпендикулярны одной и той же плоскости, значит, прямые АА0 и ВВ0 параллельны. Тогда из свойств параллельных плоскостей отрезки АА0 и ВВ0 равны.
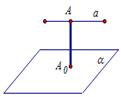 |
Расстояние между прямой и плоскостью.
Расстояние между прямой и плоскостью определяется в
случаях, когда прямая параллельна плоскости. Тогда все точки прямой а равноудалены от плоскости α. Выберем любую точку А на прямой а, опустим перпендикуляр АА0 на плоскость α. Длина перпендикуляра АА0 и называется расстоянием между прямой а и параллельной ей плоскостью α.
Обозначается: АА0= р(а; α ).
Теорема о трёх перпендикулярах.
Теорема. Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярная к самой наклонной.






|
Доказательство.
Докажем, что прямая CD перпендикулярна прямой АС:
1.Известно, что прямая АВ перпендикулярна плоскости α, АС-наклонная к плоскости α, ВС-проекция наклонной АС, прямая CD принадлежит плоскости альфа, а так же прямая CD перпендикулярна прямой ВС по построению.
2.Рассмотрим плоскость АСВ: прямая CD перпендикулярна прямой ВС по условию, а так как прямая АВ перпендикулярна плоскости альфа, значит прямая АВ будет перпендикулярна и прямой CD, лежащей в этой плоскости (по теореме о перпендилурности прямой и плоскости).
3.Прямая CD перпендикулярна к двум пересекающимся прямым АВ и ВС, принадлежащим плоскости АВС, значит прямая будет перпендикулярна и самой плоскости АВС - по признаку перпендикулярности прямой и плоскости.
4.Из признака перпендикулярности прямой и плоскости следует, что прямая CD перпендикулярна к любой прямой, лежащей в плоскости АВС, значит прямая CD перпендикулярна прямой АС ч.т.д.
 Существует так же и обратная теорема: Если провести прямую в плоскости через основание наклонной перпендикулярно к ней, то данная прямая будет перпендикулярна и к ее проекции.
Существует так же и обратная теорема: Если провести прямую в плоскости через основание наклонной перпендикулярно к ней, то данная прямая будет перпендикулярна и к ее проекции.
Угол между прямой и плоскостью.
Определение. Проекция точки на плоскость называется основание перпендикуляра, проведенного из этой точки к плоскости, если точка не лежит в плоскости, и сама точка, если она лежит в плоскости.
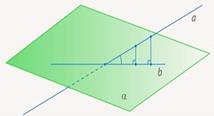 Определение. Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется
Определение. Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется
угол между прямой и ее проекцией на эту плоскость.
Чтобы построить проекцию прямой на плоскость,
достаточно опустить из любых двух ее точек
перпендикуляры на плоскость (спроектировать
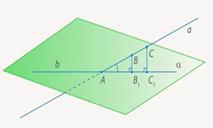 эти точки), после чего провести через них
эти точки), после чего провести через них
прямую – это и будет проекция.
Так, проекции всех точек данной прямой будут
лежать на одной прямой.
Доказательство. Пусть А - точка пересечения
прямой а и плоскости α. В и С - точки на прямой а,
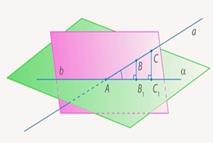
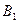 и
и  их проекции на плоскость α. Докажем, что А,
их проекции на плоскость α. Докажем, что А,
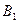 и
и  лежат на одной прямой b.
лежат на одной прямой b.
Заметим, 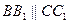 , так как
, так как 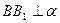 ,
,  . Значит
. Значит
если рассмотреть плоскость 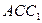 , то точки В и
, то точки В и 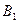
будут принадлежать ей. Но плоскость 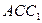
пересекает исходную плоскость по некоторой
прямой.
Значит раз точки А, 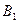 и
и  принадлежат обеим плоскостям, то они лежат на этой прямой, что и требовалось доказать.
принадлежат обеим плоскостям, то они лежат на этой прямой, что и требовалось доказать.
 6. Решение задач.
6. Решение задач.
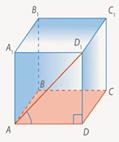
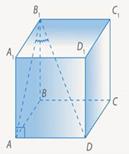
Задача 1. Рассмотрим куб 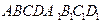 .
.
1) Необходимо найти угол между прямой 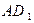 и плоскостью
и плоскостью
ABC.
Искомый угол – это угол между самой прямой и ее проекцией.
Чтобы построить проекцию прямой на плоскость, достаточно
взять две точки. Одной из них будет точка пересечения прямой и плоскости – точка А. Второй – проекция точки  – точка D, т. к. боковое ребро куба перпендикулярно плоскости основания.
– точка D, т. к. боковое ребро куба перпендикулярно плоскости основания.
Значит, искомый угол – это угол  , а он равен
, а он равен 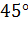 , так как это угол между диагональю и стороной квадрата.
, так как это угол между диагональю и стороной квадрата.
2) Чему равен угол между  и
и  ?
?
Чтобы построить проекцию прямой на плоскость, достаточно взять две точки. Одной из них будет точка пересечения прямой и плоскости – точка 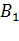 . Второй – проекция точки D – точка A, т. к. боковое ребро куба перпендикулярно плоскости основания. Значит, искомый угол –
. Второй – проекция точки D – точка A, т. к. боковое ребро куба перпендикулярно плоскости основания. Значит, искомый угол – 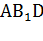 .
.
Его можно найти из треугольника 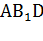 . Треугольник
. Треугольник
 Прямоугольный, так как
Прямоугольный, так как 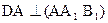 ,
, 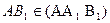 . Значит
. Значит
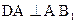 .
.
Если взять сторону куба за 1, тогда AD=1, 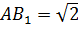 ,
,
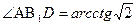
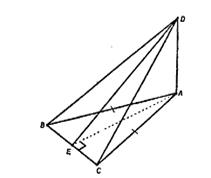 Задача 2. Отрезок АД перпендикулярен к плоскости равнобедренного треугольника АВС. Известно, что АВ =АС=5 см, ВС=6 см. АД=12 см.Найти расстояние от концов отрезка АД до прямой ВС.
Задача 2. Отрезок АД перпендикулярен к плоскости равнобедренного треугольника АВС. Известно, что АВ =АС=5 см, ВС=6 см. АД=12 см.Найти расстояние от концов отрезка АД до прямой ВС.
Дано: ΔАВС-равнобедренный
АВ=АС=5 см, ВС=6 см, АD=12 см.
Найти: АЕ, DЕ.
Решение:
1.Д.п.АЕ 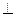 ВС
ВС
2.ΔАВС-равнобедренный→АЕ-высота и медиана→
ВЕ=ЕС=3 см
3. АЕ= 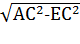 =
= 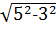 =4 см.
=4 см.
4.ВС 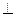 АЕ, ВС
АЕ, ВС 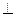 DА→ВС
DА→ВС 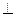 DЕ(по т.т.п.)
DЕ(по т.т.п.)
5. DЕ= 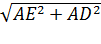 =
= 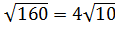 см.
см.
Ответ: АЕ=4 см. DE= 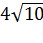 см.
см.
Задача 3. Прямая ВД перпендикулярна к плоскости треугольника АВС. Известно, что ВД=9см, АС=10 см, ВС=ВА=13 см.
 Найти расстояние:
Найти расстояние:
а)от точки Д до прямой АС;
б)площадь треугольника АСД.
Дано: ВD 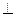 (АВС), ВD=9см
(АВС), ВD=9см
АС=10 см, ВС=ВА=13 см
Найти: DЕ, SACD
Решение:
1.Проведём ВЕ перпендикулярно АС (ВЕ 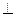 АС).
АС).
2.Так как треугольник АВС равнобедренный, то ВЕ –высота и медиана, значит СЕ=ЕА=5 см.
3.ВD 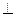 АС, ВЕ
АС, ВЕ 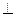 АС→DЕ
АС→DЕ 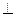 АС (по теореме о трёх перпендикулярах)
АС (по теореме о трёх перпендикулярах)
4.Расстояние от точки Д до прямой АС это отрезок ДЕ. Так как треугольник ВЕД прямоугольный, то по теореме Пифагора
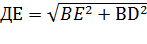 =
= 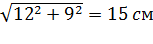
В свою очередь ВЕ можно найти из прямоугольного треугольника СВЕ:
ВЕ= 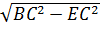 =
= 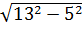 =12 см.
=12 см.
5.В треугольнике АСД: АС-основание, ДЕ - высота, тогда по формуле нахождения площади треугольника(половина произведения основания и высоты) найдем площадь треугольника АДС:
SACD=  АС*ДЕ=
АС*ДЕ=  *10*15=75см2
*10*15=75см2
Ответ:DE=15см, SACD=75см2
Контрольные вопросы
1. Что такое перпендикуляр?
2. Дайте определение наклонной.
3. Как найти расстояние между точкой и плоскостью?
4. Как найти расстояние между прямой и плоскостью?
5. Сформулируйте теорему о трёх перпендикулярах.
6. Дайте определение п роекции точки на плоскость.
7. Сформулируйте определение угла между прямой и плоскостью.
Литература
1. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10-11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни / [Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др.].- 3-е изд.- М.: Просвещение, 2016.- 255с.
Дополнительная литература
1. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е издание, исправленное и дополненное – М.: Мнемозина, 2008. – 288 с.