Проведем анализ устойчивости в Excel на примере задачи о прядильной фабрике.
Пример 2. Прядильная фабрика для производства четырех видов пряжи использует три типа сырья – чистую шерсть, капрон, акрил. В табл.1 указаны нормы расхода сырья, его общее количество, которое может быть использовано фабрикой в течение года; загрузка оборудования при производстве тонны пряжи и прибыль от реализации тонны пряжи каждого вида. Годовой ресурс оборудования составляет 140 тыс. маш.ч.
Требуется составить годовой план производства пряжи с целью максимизации суммарной прибыли.
Таблица 1. Исходные данные
| Тип сырья | Нормы расхода сырья на 1 т. пряжи | Количество сырья (т.) | |||
| Вид 1 | Вид 2 | Вид 3 | Вид 4 | ||
| Шерсть Капрон Акрил | 0,5 0,1 0,4 | 0,2 0,6 0,2 | 0,3 0,4 0,3 | 0,2 0,5 0,3 | |
| Загрузка оборудования в тыс. маш.ч | 0,06 | 0,04 | 0,03 | 0,09 | |
| Прибыль от реализации 1 т пряжи (в $) |
Обозначим:  – объем производства пряжи i-го типа в тоннах.
– объем производства пряжи i-го типа в тоннах.
Модель:

На рис. 14 представлена заполненная форма для ввода условия задачи в Excel.
Диалоговое окно «Поиск решения» для рассматриваемой задачи с введенными данными приведено на рис. 15.
| A | B | C | D | E | F | G | H | ||
| Переменные | |||||||||
| имя | x1 | x2 | x3 | x4 | |||||
| значение | |||||||||
| ЦФ | направление | ||||||||
| коэффи-циенты ЦФ | =СУММПРОИЗВ (B3:E3;B6:E6) | макс | |||||||
| ресурсы | коэффициенты | левая часть | знак | правая часть | |||||
| шерсть | 0,5 | 0,2 | 0,3 | 0,2 | =СУММПРОИЗВ (B3:E3;B10:E10) | <= | |||
| капрон | 0,1 | 0,6 | 0,4 | 0,5 | =СУММПРОИЗВ (B3:E3;B11:E11) | <= | |||
| акрил | 0,4 | 0,2 | 0,3 | 0,3 | =СУММПРОИЗВ (B3:E3;B12:E12) | <= | |||
| ресурсы оборудо-вания | 0,06 | 0,04 | 0,03 | 0,09 | =СУММПРОИЗВ (B3:E3;B13:E13) | <= | |||
Рис. 14- Форма ввода условия задачи в Excel
После нажатия кнопки «Выполнить» выдается диалоговое окно «Результаты поиска решения». Для получения отчетов по устойчивости необходимо выбрать тип отчета (можно задать все виды): «Результаты», «Устойчивость», «Пределы» и нажать кнопку «ОК» (рис. 16).

Рис. 15. Диалоговое окно «Поиск решения»

Рис. 16. Диалоговое окно «Результаты поиска решения»
Результаты решения задачи выводятся в форму ввода условий задачи: 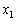 =235,29;
=235,29;  =0;
=0;  =0;
=0;  =1352,9; ЦФz=18823529,41 (рис. 17), отчеты по результатам, по устойчивости и по пределам выводятся на отдельных листах в текущей рабочей книге Excel.
=1352,9; ЦФz=18823529,41 (рис. 17), отчеты по результатам, по устойчивости и по пределам выводятся на отдельных листах в текущей рабочей книге Excel.
| A | B | C | D | E | F | G | H | |
| Переменные | ||||||||
| имя | x1 | x2 | x3 | x4 | ||||
| значение | 235,29 | 1352,9 | ||||||
| ЦФ | направление | |||||||
| коэффи-циенты ЦФ | 18823529,4 | макс | ||||||
| ресурсы | коэффициенты | левая часть | знак | правая часть | ||||
| шерсть | 0,5 | 0,2 | 0,3 | 0,2 | 388,24 | <= | ||
| капрон | 0,1 | 0,6 | 0,4 | 0,5 | 700,00 | <= | ||
| акрил | 0,4 | 0,2 | 0,3 | 0,3 | 500,00 | <= | ||
| ресурсы оборудо-вания | 0,06 | 0,04 | 0,03 | 0,09 | 135,88 | <= |
Рис. 17. Результат решения задачи
Отчет по результатам. На рис. 18 представлен отчет по результатам для задачи примера 1.
Отчет по результатам состоит из трех частей и содержит информацию о целевой функции; о значениях переменных, полученных в результате решения задачи; об ограничениях.
В отчете по результатам представлены: выражение для вычисления значения целевой функции, а также имя ЦФ, исходное значение целевой функции (до решения задачи) и значение целевой функции при оптимальном решении. Аналогичная информация приведена для всех переменных задачи: ячейка для хранения значения переменной, обозначение переменной, исходное значение и оптимальное значение.
| Microsoft Excel 11.0 Отчет по результатам | ||||||||
| Целевая ячейка (Максимум) | ||||||||
| Ячейка | Имя | Исходное значение | Результат | |||||
| $F$6 | коэффициенты ЦФ | 0,00 | 18823529,41 | |||||
| Изменяемые ячейки | ||||||||
| Ячейка | Имя | Исходное значение | Результат | |||||
| $B$3 | значение x1 | 235,29 | ||||||
| $C$3 | значение x2 | |||||||
| $D$3 | значение x3 | |||||||
| $E$3 | значение x4 | 1352,94 | ||||||
| Ограничения | ||||||||
| Ячейка | Имя | Значение | Формула | Статус | Разница | |||
| $F$12 | Акрил левая часть | 500,00 | $F$12<=$H$12 | связанное | ||||
| $F$11 | Капрон левая часть | 700,00 | $F$11<=$H$11 | связанное | ||||
| $F$10 | Шерсть левая часть | 388,24 | $F$10<=$H$10 | не связан. | 211,8 | |||
| $F$13 | Ресурсы оборудования левая часть | 135,88 | $F$13<=$H$13 | не связан. | 4,12 | |||
| $B$3 | значение x1 | 235,29 | $B$3>=0 | не связан. | 235,3 | |||
| $C$3 | значение x2 | $C$3>=0 | связанное | |||||
| $D$3 | значение x3 | $D$3>=0 | связанное | |||||
| $E$3 | значение x4 | 1352,94 | $E$3>=0 | не связан. | ||||
Рис. 18- Отчет по результатам
По ресурсам приводится следующая информация: формула, соответствующая левой части ограничения; имя ограничения; значение (величина) использованного ресурса при оптимальном решении задачи; формула, задающая ограничение; статус ограничения и разница. Если ресурс используется полностью (то есть ресурс дефицитный), то в графе «Статус» («Состояние») соответствующее ограничение указывается как «связанное»; при неполном использовании ресурса (то есть ресурс недефицитный) в этой графе указывается «не связан». В графе «Разница» показана разность между значением использованного ресурса и исходно заданной величиной ресурса. Аналогичная информация приводится по переменным задачи: оптимальное значение, статус (связанная, если оптимальное значение переменной не нулевое; несвязанная в противном случае), разность между оптимальным значением переменной и заданным для нее граничным условием.
В задаче о прядильной фабрике полученное оптимальное решение означает выпуск первого и четвертого типов пряжи (базисные переменные: 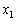 =235,29;
=235,29;  =1352,9), выпускать пряжу второго и третьего типов не выгодно (
=1352,9), выпускать пряжу второго и третьего типов не выгодно (  =0;
=0;  =0). При таком плане выпуска полностью будут использованы ресурсы (запасы) акрила и капрона, а запасы шерсти и ресурс оборудования избыточны.
=0). При таком плане выпуска полностью будут использованы ресурсы (запасы) акрила и капрона, а запасы шерсти и ресурс оборудования избыточны.
Отчет по результатам дает информацию для анализа возможного изменения запасов недефицитных ресурсов при сохранении полученного оптимального значения ЦФ. Если на ресурс наложено ограничение типа ≤, то в графе «Разница» дается количество ресурса, которое не используется при реализации оптимального решения. Например, используется 388.24 тонны шерсти. Неизрасходованным остается 211.76 тонн из общих запасов шерсти, на это количество можно уменьшить ресурс «шерсть» без изменения оптимального решения. Аналогично можно уменьшить ресурсы оборудования на 4.12 тыс. часов и это не повлияет на оптимальное решение.
Если на ресурс наложено ограничение типа ≥, то в графе «Разница» дается количество ресурса, на которое была превышена минимально необходимая норма. Если на эту величину увеличить ресурс, оптимальное решение задачи не изменится.
Отчет по устойчивости. На рис. 19 представлен отчет по устойчивости для задачи примера 1, который состоит из двух частей: информация по переменным и информация по ограничениям.
| Microsoft Excel 11.00 Отчет по устойчивости | |||||||
| Изменяемые ячейки | |||||||
| Рез. | Нормир. | Целевой | Допусти -мое | Допусти -мое | |||
| Ячейка | Имя | знач. | стоимость | Коэфф. | увели -чение | умень- шение | |
| $B$3 | x1 | 235,3 | |||||
| $C$3 | x2 | -1352,9 | 1352,94 | 1E+30 | |||
| $D$3 | x3 | -1617,7 | 1617,65 | 1E+30 | |||
| $E$3 | x4 | 1045,45 | |||||
| Ограничения | |||||||
| Рез. | Теневая | Ограни- чение | Допусти -мое | Допусти -мое | |||
| Ячейка | Имя | знач. | Цена | Правая часть | увели -чение | умень- шение | |
| $F$12 | акрил | 25294,1 | 33,33 | ||||
| $F$11 | капрон | 8823,5 | 38,89 | 514,29 | |||
| $F$10 | шерсть | 0,00 | 1E+30 | 211,76 | |||
| $F$13 | обору дование | 0,00 | 1E+30 | 4,12 |
Рис. 19- Отчет по устойчивости
Нормированная стоимость показывает, на сколько изменится значение ЦФ в случае принудительного включения единицы этой продукции в оптимальное решение. Например, в отчете по устойчивости для рассматриваемой задачи нормированная стоимость для второго вида пряжи равна: -1352.94. Это означает, что если включить в план выпуска 1 тонну пряжи второго вида, то новый план выпуска принесет прибыль на 1352.94$ меньше, чем прежний оптимальный план. Нормированная стоимость для базисных переменных всегда равна нулю.
Предельные значения приращения целевых коэффициентов. Для каждой переменной указаны заданные коэффициенты ЦФ, допустимые увеличение и уменьшение коэффициентов при которых сохраняется оптимальное решение задачи. Например, допустимое увеличение цены на пряжу первого вида равно 2875$ за тонну, а допустимое уменьшение – 8600$. Это означает, что если цена на тонну пряжи первого вида возрастет не более чем на 2875$, например станет равной 13875$, то оптимальное решение сохранится, изменится только значение ЦФ в оптимальной точке.
При выходе за указанные в отчете по устойчивости пределы изменения цен оптимальное решение может измениться как по номенклатуре выпускаемой продукции, так и по объемам выпуска (без изменения номенклатуры).
Далее в отчете по устойчивости приводится информация, относящаяся к ограничениям. В колонке «Результирующее значение» приводится величина использованных ресурсов.
Предельные значения приращения ресурсов. В графах «Допустимое уменьшение» и «Допустимое увеличение» показано на сколько можно уменьшить (устранить излишек) или увеличить (повысить минимально необходимое требование) ресурс, сохранив при этом базис оптимального решения (изменить объем выпуска продукции без изменения номенклатуры). Рассмотрим анализ дефицитных ресурсов, так как анализ недефицитных ресурсов был дан при описании отчета по результатам. В рассматриваемой задаче такими ограничениями являются дефицитные ресурсы «акрил» и «капрон». Например, если ресурсы акрила уменьшатся не более чем на 80 тонн или возрастут не более чем на 33.33 тонны, базис задачи не изменится (по-прежнему будет оптимально выпускать пряжу первого и четвертого типов, хотя объемы выпуска изменятся).
Теневая цена (ценность дополнительной единицы i-го ресурса). Теневая цена показывает насколько возрастет значение ЦФ в случае выделения дополнительной единицы i-го ресурса. Очевидно, что теневая цена не нулевая только для дефицитных ресурсов. Например, если запасы акрила возрастут на 1 тонну, прибыль увеличится на 25294,12$, если запасы капрона возрастут на 1 тонну, то прибыль будет на 8823.53$ больше, чем исходная. Поэтому в первую очередь для фабрики выгодно увеличивать запасы акрила.
В терминах теории двойственности теневая цена соответствует значению двойственной оценки соответствующего ресурса, а нормированная стоимость – значению дополнительной двойственной оценки, которая равна разности между левой и правой частями в ограничениях двойственной задачи.
Отчет по пределам. Для рассматриваемой задачи отчет по пределам приведен на рис. 20.
| Microsoft Excel 11.0 Отчет по пределам | ||||||
| Целевое | ||||||
| Ячейка | Имя | Знач. | ||||
| $F$6 | ЦФ | |||||
| Изменяемое | Ниж. | Целевой | Верх. | Целевой | ||
| Ячейка | Имя | Знач. | пред. | результат | пред. | рез. |
| $B$3 | x1 | 235,29 | 16235294,1 | 235,3 | ||
| $C$3 | x2 | 18823529,4 | ||||
| $D$3 | x3 | 18823529,4 | ||||
| $E$3 | x4 | 1352,94 | 2588235,3 | 1352,9 |
Рис. 20. Отчет по пределам
В отчете по пределам показано в каком диапазоне могут изменяться значения переменных, без изменения базиса (номенклатуры выпуска продукции). Например, если будет выпускаться 235 тонн пряжи первого вида, то в оптимальном решении ненулевые переменные будут соответствовать объемам выпуска первого и четвертого видов пряжи. В случае выпуска более чем 235.29 тонн пряжи первого типа номенклатура выпуска продукции изменится. Также в отчете по пределам приводится информация о величине ЦФ при нижнем и верхнем предельных значениях переменных задачи.
Содержание
Введение. 4
1. Настройка MS Excel 4
2. Подготовка листа с исходными данными. 5
Пример 1. 5
Порядок заполнения листа. 6
3. Установка данных для пакета «Поиск решения». 6
4. Получение результатов решения. 8
5. Типы отчетов: 9
6. Решение в Excel задач ЦЛП.. 10
7. Пример решения транспортной задачи. 11
8 Исследование устойчивости решения задачи ЛП.. 12
Анализ сокращения или увеличения ресурсов: 13
Анализ устойчивости в Excel 14