Глава III. Теория алгоритмов
Понятие "алгоритм" принадлежит к числу основных понятий математики и занимает одно из центральных мест в вычислительной математике.
Еще в IX веке арабский ученый Мухаммед бен-муса аль-Хорезми разработал систему правил четырех арифметических действий над числами в десятичной позиционной системе счисления. Эти правила предписывали строгую последовательность действий над исходными данными — числами для получения искомого результата — числа. Эти правила получили название "алгоритм" в честь арабского имени аль-Хорезми.
До 1920-х годов понятие алгоритма встречалось в математической литературе только в контексте: для решения рассматриваемой проблемы имеется алгоритм, состоящий из следующей последовательности действий - делай так, затем так и так далее и получишь требуемый результат. Иными словами, в то время пользовались интуитивным определением алгоритма: алгоритм — это общий, единообразный, точно установленный способ решения любой задачи из данной массовой проблемы - бесконечного множества однотипных задач.
Таким образом, алгоритм всегда связан с решением массовой проблемы. Задачи такого класса отличаются друг от друга значениями входящих в них параметров. Примеры алгоритмов: извлечение квадратного корня, вычисление производной, нахождение эйлерова цикла в эйлеровом графе и т.п. Приведенное определение алгоритма не является строгим, поскольку в нем встречаются слова, точный смысл которых не установлен, например "способ". Тем не менее даже при таком определении можно выделить некоторые характерныe черты алгоритма:
1. Дискретность. Алгоритм состоит из отдельных элементарных действий, выполняемых по шагам.
2. Детерминированность. Между всеми величинами, получаемыми алгоритмом, существует жесткая причинная связь. Каждая последующая величина получается из значений предыдущих по определенному, как правило, простому закону.
3. Массовость. Начальная система величин выбирается из некоторого множества. Начальные условия могут варьироваться в бесконечных пределах.
4. Результативность (сходимость). Обязательна остановка алгоритмического процесса после конечного числа шагов с указанием достигнутого конструктивного объекта в виде искомого результата.
В современной математике исходными данными и результатами работы алгоритма стали различные конструктивные объекты математики: числа и многочлены, матрицы и графы, слова и тексты. Эти конструктивные объекты формируются по определенным правилам из элементарных объектов. Происходящее за один шаг преобразование конструктивного объекта носит локальный характер, т.е преобразованию подвергается не весь объект, а лишь его часть: столбец или строка матрицы, фрагмент графа, часть слова или текста и т.п. Процесс преобразования конструктивного объекта, включающий в себя заданную последовательность шагов, называют алгоритмическим процессом.
Интуитивное понятие алгоритма работает, когда речь идет о найденном алгоритме решения конкретной проблемы. Положение существенно меняется, если возникает алгоритмическая задача, решение которой не найдено, и требуется установить, имеет ли она решение. В этом случае надо доказать либо существование алгоритма, либо его отсутствие. Первое можно сделать путем фактического описания процесса, решающего задачу. В этом случае достаточно и интуитивного понятия алгоритма, чтобы удостовериться в том, что описанный процесс есть алгоритм. Доказать несуществование алгоритма таким путем невозможно. Для этого необходимо точное формальное определение. Такого определения не было до середины тридцатых годов ХХ века. Затем почти одновременно рядом математиков были предложены несколько определений алгоритма (иными словами, была предложена формализация понятия алгоритма).
1-ое определение — через рекурсивные функции — связывает понятие алгоритма с числовыми функциями, определяемыми на множестве целых положительных чисел и принимающими значения на том же множестве (американские математики А. Чёрч и С.К. Клини, опираясь на более ранние работы Ж. Эрбрана и К. Гёделя).
2-ое определение — машина Тьюринга — связывает понятие алгоритма с механическим устройством, способным выполнять дискретно элементарные действия над элементарными объектами (английский математик A.M. Тьюринг[1]).
3-е определение - в виде некоторого набора правил, называемых системой продукций (предложил американский математик Э. Пост)
4-ое определение — нормальный алгоритм Маркова — связывает понятие алгоритма с классом словарных преобразований в результате замены части слова или всего слова другим (А.А. Марков[2]).
Существование различных определений понятия алгоритма имеет и свои преимущества, т.к. для решения различных задач удобно использовать различные наиболее подходящие для этого случая определения.
Доказать, что предложенные математически строгие конструкции действительно являются формализацией содержательного понятия алгоритма нельзя, так как, с одной стороны, имеются строгие определения, а с другой - наши инструктивные представления о понятии алгоритма, которые не могут быть предметом математического рассмотрения.
Такая ситуация не является необычной для математики и возникла не впервые - многие математические определения являются формализацией наших содержательных представлений о рассматриваемых явлениях. Например, строгое математическое определение непрерывности функции f (z) на отрезке [ а,b ] 

конкретизирует наше представление о непрерывности линий, являющихся графиками этих функций.
В том, что предложенные определения понятия алгоритма являются тем, что нужно, и соответствуют содержательным математическим представлениям, нас убеждают следующие факты.
Во-первых, было доказано, что все предложенные строгие определения понятия алгоритма, несмотря на их совершенно различные формы, эквивалентны между собой. То есть, если существует алгоритм в смысле одного определения, то существуют алгоритмы и в смысле всех других определений.
Во-вторых, любой из известных в математике алгоритмов, а таких алгоритмов за многие годы существования математики накопилось достаточно много, может быть формализован в рамках предложенных определений. И совершенно не видно, как может быть задан алгоритм, не укладывающийся в рамки этих формализации.
В-третьих, все дальнейшее, базирующееся на этих определениях развитие теории алгоритмов, убеждает нас в правильности Предложенных определений.
После того как формальное определение понятия алгоритма было дано, появилась возможность доказывать, что некоторые массовые проблемы не имеют алгоритмического решения. И такие доказательства действительно были почти сразу получены. Первое из них (1936 г.) принадлежит А. Черчу. Он показал, что исчисление предикатов алгоритмически неразрешимо. Заметим, что отсутствие алгоритма решения массовой проблемы не означает, что нельзя решить каждую конкретную задачу этой проблемы, а свидетельствует лишь об отсутствии единого метода решения всех этих задач.
Каждому из вышеприведенных 4 определений алгоритма соответствует свой тип универсальной алгоритмической модели. Далее рассмотрим подробнее первые два типа моделей.
Список упражнений по теме “Теория алгоритмов”
26. Какая функция получается из j и y с помощью схемы примитивной рекурсии, если:
а)  ,
,  ; б)
; б)  ,
, 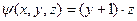 ?
?
27. Доказать, что следующие функции примитивно рекурсивны:
а)  , б)
, б) 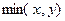 , в)
, в)  , г)
, г) 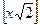 ,
,
д)  - число делителей числа х, где
- число делителей числа х, где  .
.
28. Определите следующие функции с помощью ограниченного оператора минимизации
а)  ; б)
; б)  .
.
29. Доказать равенства  , если
, если
а)  ,
,  ; б)
; б)  ,
, 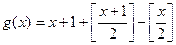 .
.
30. Составьте программу “левый сдвиг” для машины Тьюринга с алфавитом А ={0, 1}:
01 xq 10Þ q 001 x 0.
31. Машина Тьюринга Т работает в алфавите А ={l, 0, 1}. Множество внутренних состояний машины Q ={ q 1, q 2}. Функциональная схема этой машины представлена в таблице.
| l | |||
| q 1 | 1 Rq 1 | 0 Cq 0 | 1 Rq 2 |
| q 2 | 1 Rq 2 | 1 Rq 2 | 1 Rq 2 |
К каким исходным словам не применима данная машина?
32. Построить машины Тьюринга для вычисления следующих функций в унарной системе счисления:
а) O (x)=0, т.е. q101 x 0Þq000 x +1;
б)  , т.е. q101 x 0Þq001 x +10;
, т.е. q101 x 0Þq001 x +10;
в)  , если q101 x 0Þq00
, если q101 x 0Þq00  ;
;
г)  для исходного состояния q101 x 0 (х – натуральное число).
для исходного состояния q101 x 0 (х – натуральное число).
33. Построить машину Тьюринга для вычисления функции 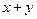 , т.е. 0q11 x 01 y 0Þq001 x+y 0.
, т.е. 0q11 x 01 y 0Þq001 x+y 0.
34. Построить машину Тьюринга, реализующую алгоритм вычисления функции  в десятичной системе счисления.
в десятичной системе счисления.
[1] Алан Матисон Тьюринг (1912-1954) - английский математик и логик.
Эмиль Леон Пост (1897-1954), Алонзо Черч (1903-1995), Стефен Коул Клини (1909-1994) - американские математики и логики; Жак Эрбран (1908-1931) - французский математик и логик.
Курт Гедель (1906-1978) - математик и логик. Родился в Австро-Венгрии. С 1940 г. жил в США.
[2] Андрей Андреевич Марков (1903-1979) – член-корреспондент АН СССР.