Коэффициент корреляции Пирсона (r-Пирсона) применяется для исследования взаимосвязи двух переменных, измеренных в метрических шкалах на одной и той же выборке. Он позволяет определить, насколько пропорциональная изменчивость двух переменных.
Данный коэффициент разработали Карл Пирсон, Фрэнсис Эджуорт и Рафаэль Уэлдон в 90-х годах XIX века. Коэффициент корреляции изменяется в пределах от минус единицы до плюс единицы.
Коэффициент корреляции r-Пирсона характеризует существование линейной связи между двумя величинами. Если связь криволинейная то он не будет работать.
Чтобы приступать к расчетам коэффициента корреляции r-Пирсона необходимо выполнение следующих условий:
- Исследуемые переменные X и Y должны быть распределены нормально (что это значит - переменные должны образовывать двумерное нормальное распределение, когда большинство объектов группируются вокруг среднего).
- Исследуемые переменные X и Y должны быть измерены в интервальной шкале или шкале отношений.
- Количество значений в исследуемых переменных X и Y должно быть одинаковым.
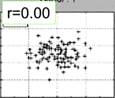
| При расчете коэффициент линейной корреляции Пирсона используется специальная формула (на уроке не рассматривается). Величина коэффициента корреляции варьируется от 0 до 1. ρ = 0,1 - слабая корреляция; ρ = 0,3 – корреляция средней силы; ρ = 0,5 - сильная корреляция. Слабыми сторонами линейного коэффициента корреляции Пирсона являются: Неустойчивость к выбросам. С помощью коэффициента корреляции Пирсона можно определить только силу линейной взаимосвязи между переменными, другие виды взаимосвязей выявляются методами регрессионного анализа. Две характеристики: – наклон (направление связи) и ширина (сила связи) воображаемого эллипса. Слабее связь – шире эллипс. Примеры ↓→ | 
| |||
| 
| 
| 
| |
На Практической работе № 17 вами были выполнены расчеты корреляционных зависимостей. Работа выполнялась с использованием электронных таблиц LibreOffice Calc. Вспомните порядок выполнения практической работы и те выводы, которые, которые были сделаны Вами (далее в таблице приводится практическая работа № 17)!
| Задание 1 Выполнить расчеты корреляционной зависимости успеваемости учащихся от хозяйственных расходов школы, описанные в § 19 учебника. 1. Заполнить электронную таблицу следующими данными: 2. Построить точечную диаграмму зависимости величин (ее вид показан в учебнике на рис. 6.7). 3. Выполнить статистическую функцию КОРРЕЛ, указав в диалоговом окне диапазоны значений: В2:В21 и С2:С21. 4. Выписать значение коэффициента корреляции. Синтаксис статистической функции: =КОРРЕЛ(массив1;массив2) В нелокализованной версии=CORREL(array1; array2) Выводы: Эта величина говорит о среднем уровне корреляции. Наличие зависимости между хозяйственными затратами школы и успеваемостью нетрудно понять. Ученики с удовольствием ходят в чистую, красивую, уютную школу, чувствуют там себя, как дома, и поэтому лучше учатся. |
Результат р = 0,500273843 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Задание 2
Выполнить расчеты корреляционных зависимостей успеваемости учащихся от обеспеченности учебниками и от обеспеченности компьютерами, представленными в следующей таблице: Обеспечение учебного процесса
Полученные значения коэффициентов корреляции сопоставить с приведенными в § 19 учебника (Результат ρ = 0,500273843 ρ =0,780931,0,572465) Выводы: Как видно из таблицы, корреляция между обеспеченностью учебниками к успеваемостью сильнее, чем корреляция между компьютерным обеспечением и успеваемостью (хотя и тот, и другой коэффициенты корреляции не очень большие). Отсюда можно сделать вывод, что пока еще книга остается более значительным источником знаний, чем компьютер. |
II. Выполнение практической работы № 18 Данная работа выполняется по рекомендациям, изложенным в учебнике по информатике 11 класс на стр. 215 – 216, задание:
Придумать таблицу парных измерений значений некоторых величин, между которыми существует гипотетическая корреляционная зависимость. Провести анализ этой зависимости на наличие линейной корреляции.
Примерами соответствующих связанных величин могут служить:
• уровень образования (измеренный, например, в годах обучения в целом) и уровень месячного дохода;
• уровень образования и уровень занимаемой должности (для последней придумайте условную шкалу);
• количество компьютеров в школе, приходящихся на одного учащегося, и средняя оценка при тестировании на уровень владения стандартными технологиями обработки информации;
Практикум
• количество часов, затрачиваемых старшеклассниками на выполнение домашних заданий, и средняя оценка;
• количество удобрений, вносимых в почву, и урожайность той или иной сельскохозяйственной культуры.
При этом вы можете идти двумя путями.
Первый, более серьезный и практически полезный: вы не просто придумываете гипотетическую
корреляционную зависимость, но и находите в литературе действительные данные о ней.
Второй путь, более легкий: вы рассматриваете это как игру, необходимую для понимания того, что такое корреляционная зависимость, и выработки технических навыков ее анализа, и придумываете соответствующие
данные, стараясь делать это наиболее правдоподобным образом.
Воспользовавшись рекомендациями, целесообразно обратиться к источникам в открытом доступе, в частности в сети Интернет. Для выполнения задания, как вариант выполнения задания, были загружены научные работы (см. вложение). Для примера ниже представлены решения нескольких задач в MS Excel.
| Пример № 1. О сусликах (данный материал может быть использован при выполнении ПР. № 18): Условие задачи: Необходимо проанализировать взаимосвязь между двумя переменными – X и Y. Мы исследуем сусликов. И хотим узнать, как связаны у них масса тела и длина хвоста? Переменные – 1. масса тела; 2. длина хвоста. |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение: В чём смысл корреляции: мы хотим понять, в какой степени две переменные СОВМЕСТНО ИЗМЕНЯЮТСЯ: если суслик очень тяжёлый, значит ли это, что и хвост у него длинный? А может, наоборот, короткий? Корреляции Если значения одной переменной растут, другой – тоже растут? Уменьшаются? Не изменяются? Внутри каждой переменной есть изменчивость – большие и маленькие отклонения от среднего. И надо бы, чтоб коэффициент не зависел от размерности переменных.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример № 2. Сравнительная оценка факторов посредством анализа парных коэффициентов корреляции (использованы материалы статьи Н. Б. Громовой «Прогноз объема перевозок грузов по совокупным итогам 2013 и 2014 годов на основе синергетической теории управления»).
Дано:
Необходимо: Выполнить сравнительную оценку факторов посредством анализа парных коэффициентов корреляции, после чего оценить их значимость. Итоговым показателе Y принят объем перевозок, влияющими факторами приняты Х1, Х2, Х3, Х4, Х5, Х6.
Решение: Коэффициенты парной корреляции позволяют установить наличие и характер зависимости между заданными факторами, а также оценить, насколько верно выбранные факторы отражают. Для этого составим матрицу парных коэффициентов корреляции, измеряющих тесноту связи каждого признака Xn с результирующим показателем Y.
Используется статистическая функция =КОРРЕЛ(B3:B15;H3:H15)
Наибольшее прямое влияние на объем перевозок имеет производительность подвижного состава (0,8755), наиболее сильное обратное влияние имеет средняя дальность перевозок (-0,8524). Остальные коэффициенты корреляции находятся на уровне средней корреляции. Коэффициент корреляции для Х5 (рентабельность перевозок 0,5943) целесообразно и можно исключить из исследования, т.к. является показатель Х5 сам является производным от прибыли и себестоимости. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример № 3. Формирование корреляционной матрицы показателей сельскохозяйственного производства Приморского края(для данной задачи использована статья Е. М. Дроздовой, старшего преподавателя,
кафедра управления персоналом и экономики труда, Дальневосточный федеральный университет, г. Владивосток) «Корреляционно-регрессионный анализ показателей сельскохозяйственного производства Приморского края».
Дано:
Значение показателей сельскохозяйственной отрасли для корреляционно-регрессионного анализа (2005-2011 гг.)
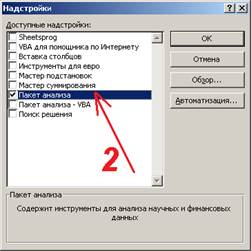
Решение: Для формирования корреляционной матрицы необходимо использовать надстройку MS Excel «Пакет анализа». Если на вкладке «Данные» отсутствует «Анализ данных», необходимо через «Параметры Excel» подключить надстройку «Пакет анализа» (см. шаги 1, 2, 3). Далее выполнить шаг 4 (выбрать «Корреляция»), шаг 5 (выбрать диапазон анализируемых данных). Шаг 6 – получение корреляционной матрицы, формирование выводов.
Шаг 7 – Сделать выводы:
Как видно из данных матрицы, существует достаточно высокая и положительная (прямая) связь показателей производительности труда (0,999), урожайности (0,986), объема используемых основных фондов (0,949) и фондоотдачи (0,916) с показателем объема производства в сопоставимых ценах. Учитывая, что анализ производился по статистическим данным сельскохозяйственной отрасли, можно отметить справедливость выявленных взаимосвязей. Между тем, показатели количества занятых (-0,504) и посевной площади (-0,071) находятся в обратной и умеренной или слабой зависимости с объемом производства в сопоставимых ценах, что позволяет принять решение об исключении указанных факторов в дальнейшем анализе. Также стоит указать на обнаруженную высокую тесноту связи между показателями урожайности (0,986), объема используемых основных фондов (0,951), фондоотдачи (0,914) и показателем производительности труда. |
Шаг 1
Шаг 2
Шаг 3
Шаг 4
Шаг 5
Шаг 6 - Получение результата
III. Домашнее задание -
1) используя § 19 учебника, конспект урока и любые источники, выполнить два примера ПР № 18, согласно условия (см. синий шрифт).
2) до 09.04.2020 на эл. адрес tihomirov63@mail.ru прислать не менее двух примеров ПР № 18 в формате файлов MS Excel или LibreOffice Calc (рассчитать значения коэффициентов корреляции, сделать выводы).
IV. Дополнительный материалы:
https://youtu.be/wGTIjN4KeJs
https://youtu.be/xIxFFsQ9Jlo
https://youtu.be/Z6_aRLb8RQk
https://youtu.be/a_qpWdy-Gxo
https://youtu.be/HfNtbxYVBE0
https://youtu.be/2e6EStpZwIU