Основные теоретические положения

Работа №2

ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА

Цель работы

Получение навыков сборки простых электрических цепей, включения в электрическую цепь измерительных приборов.

Научиться измерять токи и напряжения, убедиться в соблюдении законов Ома и Кирхгофа в линейной электрической цепи.

Исследовать влияние изменения параметров одного потребителя на режим работы других потребителей при последовательном, параллельном и смешанном соединенях.

 

Основные теоретические положения

2.1. Основные понятия

Все электрические цепи делятся на линейные и нелинейные.

Элемент электрической цепи, параметры которого (сопротивление и др.) не зависят от тока в нем, называют линейным, например электропечь.

Нелинейный элемент, например лампа накаливания, имеет сопротивление, величина которого увеличивается при повышении напряжения, а следовательно и тока, подводимого к лампочке.

Следовательно, в линейной электрической цепи все элементы – линейные, а нелинейной называют электрическую цепь, содержащую хотя бы один нелинейный элемент.

При расчете в схеме электрической цепи выделяют несколько основных элементов (рис. 2.1).

 

Рис. 2.1. Схема электрической цепи

Ветвь электрической цепи (схемы) – участок цепи с одним и тем же током. Ветвь может состоять из одного или нескольких последовательно соединенных элементов (рис. 2.2).

Рис. 2.2. Ветвь электрической цепи

Схема на рис. 2.1 имеет три ветви: ветвь bma, в которую включены элементы r₀, E, R и в которой возникает ток I; ветвь ab с элементом R₁ и током I₁; ветвь anb с элементом R₂ и током I₂.

Узел электрической цепи (схемы) – место соединения трех и более ветвей (точка, в которой сходятся не менее трех токов). В схеме на рис. 2.1 – два узла a и b. Ветви, присоединенные к одной паре узлов, называют параллельными. Сопротивления R₁ и R₂ (рис. 2.1) находятся в параллельных ветвях.

Контур – любой замкнутый путь, проходящий по нескольким ветвям. В схеме на рис. 2.1 можно выделить три контура: I – bmab; II – anba; III – manbm, на схеме стрелкой показывают направление обхода контура.

Источник ЭДС на электрической схеме (рис. 2.1.) может быть заменен источником напряжения U, причем условное положительное направление напряжения U источника задается противоположным направлению ЭДС.

Условные положительные направления ЭДС источников питания, токов во всех ветвях, напряжений между узлами и на зажимах элементов цепи необходимо задать для правильной записи уравнений, описывающих процессы в электрической цепи или ее элементах.

На схеме (рис. 2.1) стрелками укажем положительные направления ЭДС, напряжений и токов:

а) для ЭДС источников – произвольно, но при этом следует учитывать, что полюс (зажим источника), к которому направлена стрелка, имеет более высокий потенциал по отношению к другому полюсу;

б) для токов в ветвях, содержащих источники ЭДС – совпадающими с направлением ЭДС; во всех других ветвях произвольно;

в) для напряжений – совпадающими с направлением тока в ветви или элементе цепи.

2.2. Основные законы цепей постоянного тока

Расчет и анализ электрических цепей производится с использованием закона Ома, первого и второго законов Кирхгофа. На основе этих законов устанавливается взаимосвязь между значениями токов, напряжений, ЭДС всей электрической цепи и отдельных ее участков и параметрами элементов, входящих в состав этой цепи.

Закон Ома для участка цепи

Соотношение между током I, напряжением U_R и сопротивлением R участка mа электрической цепи (рис. 2.1) выражается законом Ома

или U_R = RI.

 

В этом случае U_R = RI – называют напряжением или падением напряжения на резисторе R, а I – током в резисторе R.

При расчете электрических цепей иногда удобнее пользоваться не сопротивлением R, а величиной обратной сопротивлению, т.е. электрической проводимостью:

.

В этом случае закон Ома для участка цепи запишется в виде:

I = Ug.

Сложная электрическая цепь содержит, как правило, несколько ветвей, в которые могут быть включены свои источники питания и режим ее работы не может быть описан только законом Ома. Но это можно выполнить на основании первого и второго законов Кирхгофа, являющихся следствием закона сохранения энергии.

Первый закон Кирхгофа

В любом узле электрической цепи алгебраическая сумма токов равна нулю

,

где m – число ветвей, подключенных к узлу.

При записи уравнений по первому закону Кирхгофа токи, направленные к узлу, берут со знаком «плюс», а токи, направленные от узла – со знаком «минус». Например, для узла а (см. рис. 2.1) I – I₁ – I₂ = 0.

Второй закон Кирхгофа

В любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех его участках

,

где n – число источников ЭДС в контуре; m – число элементов с сопротивлением R_к в контуре; U_к = R_кI_к – напряжение или падение напряжения на к-м элементе контура.

Для схемы (рис. 2.1) запишем уравнение по второму закону Кирхгофа, для контура I:

E = U_R + U₁.

Если в электрической цепи включены источники напряжений, то второй закон Кирхгофа формулируется в следующем виде: алгебраическая сумма напряжений на всех элементах контура, включая источники ЭДС, равна нулю

.

При записи уравнений по второму закону Кирхгофа необходимо:

1) задать условные положительные направления ЭДС, токов и напряжений;

2) выбрать направление обхода контура, для которого записывается уравнение;

3) записать уравнение, пользуясь одной из формулировок второго закона Кирхгофа, причем слагаемые, входящие в уравнение, берут со знаком «плюс», если их условные положительные направления совпадают с обходом контура, и со знаком «минус», если они противоположны.

Запишем уравнения по II закону Кирхгофа для контуров электрической схемы (рис. 2.1):

контур I: E = RI + R₁I₁ + r₀I,

контур II: R₂I₂ - R₁I₁ = 0,

контур III: E = RI + R₂I₂ + r₀I.

В действующей цепи электрическая энергия источника питания преобразуется в другие виды энергии. На участке цепи с сопротивлением R в течение времени t при токе I расходуется электрическая энергия

W = I²Rt.

Скорость преобразования электрической энергии в другие виды представляет электрическую мощность

.

Из закона сохранения энергии следует, что мощность источников питания в любой момент времени равна сумме мощностей, расходуемой на всех участках цепи.

.

Это соотношение называют уравнением баланса мощностей. При составлении уравнения баланса мощностей следует учесть, что если действительные направления ЭДС и тока источника совпадают, то источник ЭДС работает в режиме источника питания, и произведение E I подставляют в уравнение баланса со знаком плюс. Если не совпадают, то источник ЭДС работает в режиме потребителя электрической энергии, и произведение E I подставляют в уравнение баланса со знаком минус. Для цепи, показанной на рис. 1.2 уравнение баланса мощностей запишется в виде:

EI = I²(r₀ + R) + I₁²R₁ + I₂²R₂.

При расчете электрических цепей используются определенные единицы измерения. Электрический ток измеряется в амперах (А), напряжение – в вольтах (В), сопротивление – в омах (Ом), мощность – в ваттах (Вт), электрическая энергия – ватт-час (Вт-час) и проводимость – в сименсах (См).

Кроме основных единиц используют более мелкие и более крупные единицы измерения: миллиампер (1мA = 10^–3А), килоампер (1кA = 10³А), милливольт (1мВ =10^–3В), киловольт (1кВ = 10³В), килоом (1кОм = 10³Ом), мегаом (1мОм = 10⁶Ом), киловатт (1кВт = 10³Вт), киловатт-час (1кВт-час = 10³ ватт-час).

2.3. Способы соединения сопротивлений и расчет эквивалентного сопротивления электрической цепи

Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник». Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением R_экв, и вся схема представляется в виде схемы на рис. 2.3 б, а расчет токов и напряжений производится с помощью законов Ома и Кирхгофа.

Электрическая цепь с последовательным соединением элементов

Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 2.3 а).

На основании второго закона Кирхгофа общее напряжение U всей цепи равно сумме напряжений на отдельных участках:

U = U₁ + U₂ + U₃ или IR_экв = IR₁ + IR₂ + IR₃,

откуда следует

R_экв = R₁ + R₂ + R₃.

а)	б)
Рис. 2.3. Последовательное соединение элементов

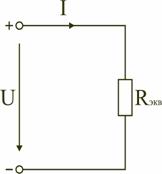
Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением R_экв (рис. 2.3 б)). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома

,

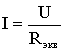и по вышеприведенным формулам рассчитывают падение напряжений U₁, U₂, U₃ на соответствующих участках электрической цепи (рис. 2.3 а).

Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.

Электрическая цепь с параллельным соединением элементов

Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 2.4).

Рис. 2.4. Параллельное соединение элементов.

В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:

I = I₁ + I₂ + I₃,

откуда следует, что

.

Из этого соотношения, следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:

g_экв = g₁ + g₂ + g₃.

 

В том случае, когда параллельно включены два сопротивления R₁ и R₂, они заменяются одним эквивалентным сопротивлением

.

По мере роста числа параллельно включенных потребителей проводимость цепи g_экв возрастает, и наоборот, общее сопротивление R_экв уменьшается.

Напряжение в электрической цепи с параллельно соединенными сопротивлениями (рис. 2.4.)

U = IR_экв = I₁R₁ = I₂R₂ = I₃R₃.

Отсюда следует, что

,

т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.

По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.

Электрическая цепь со смешанным соединением элементов

Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.

Рис. 2.5. Смешанное соединение элементов

Для цепи, представленной на рис. 2.5, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R₁=R₂=R₃=R₄=R₅=R. Сопротивления R₄ и R₅ включены параллельно, тогда сопротивление участка цепи cd равно:

.

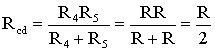В этом случае исходную схему (рис. 2.5) можно представить в следующем виде (рис. 2.6):

Рис. 2.6. Упрощение схемы рис.2.5.

 

На схеме (рис. 2.6.) сопротивление R₃ и R_cd соединены последовательно, и тогда сопротивление участка цепи ad равно:

.

Тогда схему (рис. 2.6.) можно представить в сокращенном варианте (рис. 2.7.):

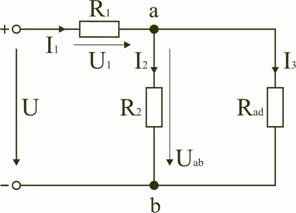
Рис. 2.7. Упрощение схемы рис. 2.6

 

На схеме (рис. 2.7) сопротивление R₂ и R_ad соединены параллельно, тогда сопротивление участка цепи аb равно

.

Схему (рис. 2.7) можно представить в упрощенном варианте (рис. 2.8), где сопротивления R₁ и R_ab включены последовательно.

Тогда эквивалентное сопротивление исходной схемы (рис. 2.5.) будет равно:

.

Рис. 2.8. Упрощение схемы рис. 2.7.	Рис. 2.9. Упрощение схемы рис. 2.8.

 

В результате преобразований исходная схема (рис. 2.5) представлена в виде схемы (рис. 2.9) с одним сопротивлением R_экв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.

 

3. Описание лабораторной установки.

В лабораторной работе исследуются электрические цепи постоянного тока с разными вариантами соединения резисторов R₁, R₂, R₃. Принципиальные электрические схемы экспериментов и их монтажные схемы для последовательного соединения резисторов приведены на рис 2.10, 2.11, для параллельного – на рис. 2.12, 2.13, для смешанного – на рис. 2.14, 2.15.

Экспериментальные исследования линейных электрических цепей выполняется на стенде «Электрические цепи» учебно-исследовательского комплекса «Электротехника и электромеханика – 1,5 кВт». Для проведения лабораторной работы используется оборудование стендов (рис. 2.11, 2.13, 2.15)

1. Модуль питания (напряжение +5В,+12В,-12В).

2. Модуль резисторов (переменные резисторы R₁, R₂, R₃ с сопротивлением 5,10,20,30,40,50 Ом).

3. Модуль измерительный (цифровые амперметры).

4. Модуль цифровых мультиметров.

5. Модуль «Измеритель мощности».

Модуль питания используется в качестве источника постоянного напряжения +12 В. На модуле резисторов выставляются, заданные значения сопротивлений резисторов R₁, R₂, R₃, согласно варианту (табл.2.1). Для измерения токов при параллельном и смешанном соединении используется модуль цифровых амперметров, включаемых на измерение постоянного тока. Для измерения напряжения на отдельных элементах схемы используется модуль цифровых мультиметров. Измеритель мощности позволяет измерить напряжение, ток и активную мощность на входе электрической цепи.

 

Расчетное задание.

Для выполнения расчетного задания необходимо изучить тему «Линейные электрические цепи постоянного тока», содержание данной лабораторной работы и подготовить ответы на контрольные вопросы.

Расчётное задание выполняется при подготовке к лабораторной работе в соответствии с заданным вариантом (табл. 2.1). В процессе его выполнения необходимо рассчитать электрические цепи с последовательным, параллельным и смешанным соединением элементов.

Таблица 2.1.

Вариант
U,В
R1,Ом
R2,Ом
R3,Ом

4.1. Расчет электрической цепи с последовательным соединением

резисторов.

На основе схемы эксперимента (рис.2.10) нарисовать расчетную схему электрической цепи, указать на ней ток и все напряжения. Произвести расчет схемы, используя законы Ома и Кирхгофа для данных своего варианта (табл.2.1) для двух режимов работы с разными значениями сопротивления резистора R₂. Полученные в обоих случаях значения потребляемых из сети тока I, активной мощности P, напряжения на каждом элементе цепи U₁, U₂, U₃, эквивалентного сопротивления R_э занести в табл. 2.2 в графу расчет. Проверить выполнение 2 закона Кирхгофа.

4.2. Расчет электрической цепи с параллельным соединением

резисторов.

На основе схемы эксперимента (рис.2.12) нарисовать расчетную схему электрической цепи, указать на ней напряжение и все токи. Используя данные своего варианта (табл.2.1), по законам Ома и Кирхгофа рассчитать: токи I₁, I₂, I₃ и ток I всей цепи; эквивалентное сопротивление всей цепи R_э; активную мощность P, потребляемую цепью из сети. Полученные значения занести в табл.2.3, в графу расчет. Проверить выполнение первого закона Кирхгофа. Расчет произвести для двух режимов работы электрической цепи с разными значениями резистора R₂.

4.3. Расчет электрической цепи со смешанным соединением

резисторов.

На основе схемы эксперимента (рис.2.14) нарисовать расчетную схему электрической цепи, указать на ней напряжение и все токи. Используя данные своего варианта (табл.2.1), рассчитать: эквивалентное сопротивление всей цепи R_э; по законам Ома и Кирхгофа рассчитать ток I₁ всей цепи и токи I₂, I₃ в параллельных ветвях с резисторами R₂, R₃; напряжение U₂₃ в этих ветвях; напряжение U₁ на резисторе R₁; а также активные мощности P₁, P₂, P₃, расходуемые на каждом элементе и мощность всей цепи P. Полученные значения занести в табл.2.4, в графу «расчет». Проверить выполнение условия баланса мощностей для данной схемы. Расчет произвести для двух режимов работы электрической цепи с разными значениями резистора R₂.

 

 

Экспериментальная часть

Ознакомиться с лабораторной установкой: модуль питания, модуль резисторов, модуль мультиметров, модуль измерительный (модуль амперметров) измеритель мощности.

 

5.1. Последовательное соединение резисторов.

На рис. 2.10 приведена принципиальная электрическая схема электрической цепи с последовательным соединением резисторов R₁, R₂, R_3. Используя монтажную схему (рис 2.11) собрать электрическую цепь с последовательным соединением резисторов. Установить переключатели SA1, SA2, SA3 в соответствии с заданным вариантом (табл.2.1). Измеритель мощности перевести в режим измерения постоянного тока и установить на нем пределы по напряжению «30В», по току «2А», мультиметр – в режим измерения постоянного напряжения. Предоставить схему для проверки преподавателю.

После проверки схемы включить электропитание стенда (автоматический выключатель QF модуля питания) и измерителя мощности (выключатель «Сеть»). Включить источник постоянного напряжения (выключатель SA2 модуля питания). С помощью измерителя мощности измерить напряжение питания U, входной ток I, потребляемую нагрузкой активную мощность P. Мультиметром измерить напряжение U₁, U₂, U₃ на резисторах R₁, R₂, R₃.

Таблица 2.2.

Параметры	U	I	P	U1	U2	U3	R1	R2	R3	Rэ
В	А	Вт	В	В	В	Ом	Ом	Ом	Ом
Расчет
Эксперимент
Расчет
Эксперимент

 

Результаты измерений занести в табл. 2.2. в графу «эксперимент». Изменить величину сопротивления R2 и снова провести аналогичные измерения. Выключить питание. По результатам измерений вычислить сопротивление каждого потребителя (R1, R2, R3) и общее (эквивалентное) сопротивление R_Э цепи. Результаты вычислений занести в табл. 2.2.

Сравнить результаты измерений и расчетов, убедиться в том, что сумма сопротивлений отдельных потребителей равна сопротивлению всей цепи. Убедиться в соблюдении второго закона Кирхгофа. Объяснить изменение режима работы цепи и отдельных потребителей при изменении величины сопротивления одного из резисторов.

 

 

 

 

 

Рис. 2.10. Принципиальная электрическая схема с последовательным соединением резисторов.

 

 

 

 

 

Рис. 2.11. Последовательное соединение резисторов. Монтажная схема.

5.2. Параллельное соединение резисторов.

На рис. 2.12 приведена принципиальная электрическая схема электрической цепи с параллельным соединением резисторов R₁, R₂, R_3. Используя монтажную схему (рис. 2.13) собрать электрическую цепь с параллельным соединением резисторов.

Установить переключатели SA1, SA2, SA3 модуля резисторов в соответствии с заданным вариантом (табл.2.1), измерительный модуль (модуль амперметров) перевести в режим измерения постоянного тока. После проверки собранной цепи включить электропитание стенда, измери­тель мощности и измерительный модуль амперметров. С помощью измерителя мощности PP1 измерить напряжение U и то­к I, активную мощность Р всей цепи, амперметрами PA1, PA2, PA3 – токи I₁, I₂, I₃ в соответствующих резисторах. Результаты измерений занести в табл. 2.3 в графу «эксперимент».

Изменить в соответствии с заданным вариантом величину сопротивления R₂ и снова провести измерения. Выключить электропитание. По результатам измере­ний рассчитать сопротивления резисторов R₁, R₂, R₃ и сопротивление всей цепи R_э, Результаты вычис­лений занести в табл. 2.3. Убедиться в соблюдении первого закона Кирхгофа. Сделать вывод об изменении режима работы цепи и отдельных потребителей при изменении величины сопротивления резистора R₂.

Таблица 2.3

Параметры	U	I	I1	I2	I3	P	R1	R2	R3	RЭ
В	А	А	А	А	Вт	Ом	Ом	Ом	Ом
Расчет
Эксперимент
Расчет
Эксперимент

 

Рис. 2.12. Принципиальная электрическая схема с параллельным соединением резисторов

 

Рис.2.13. Параллельное соединение резисторов. Монтажная схема

6.3. Смешанное соединение резисторов.

На рис. 2.14 приведена принципиальная электрическая схема электрической цепи со смешанным соединением резисторов R₁, R₂, R₃.

Используя монтажную схему соединения (рис 2.15) собрать электрическую цепь со смешанным соединением резисторов. Установить переключатели SA1, SA2, SA3 модуля резисторов в соответствии с заданным вариантом (табл.2.1). После проверки схемы преподавателем вклю­чить электропитание стенда, измеритель мощности и модуль амперметров. Измерителем мощности PP1 измерить напряжение U, ток I₁ и мощность P всей цепи. Амперметрами PA1 и PA2 измерить токи I₂,I₃ резисторов R₂, R₃. Мультиметром измерить напряжение U₂₃ на параллельно включенных резисторах R₂, R₃ и напряжение U₁ на резисторе R₁. Результаты измерений занести в табл. 2.4 в графу «эксперимент». Установить новое значение резистора R₂ и снова измерить напряжения и то­ки в цепи. Выключить электропитание. По результатам измерений вычислить мощность каждого участка цепи Р₁, Р₂, Р₃, определить эквивалентное сопротивление цепи R_э. Результаты вычислений занести в табл. 2.4. Проверить выполнение баланса мощностей в исследуемой цепи. Сде­лать вывод об изменении режима работы цепи и отдельных потребителей при из­менении величины резистора R₂.

 

Таблица 2.4

Параметр	U	U23	U1	I1	I2	I3	Р	Р1	Р2	Р3	Rэ
В	В	В	А	А	А	Вт	Вт	Вт	Вт	Ом
Расчет
Эксперимент
Расчет
Эксперимент

 

 

 

Рис. 2.14. Принципиальная электрическая схема со смешанным соединением резисторов

 

 

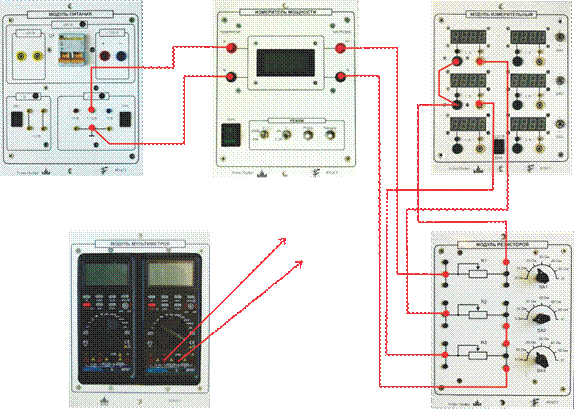
Рис 2.15. Смешанное соединение резисторов. Монтажная схема

 

 

Содержание отчёта.

Отчёт по работе должен содержать:

6.1. Наименование работы и цель работы.

6.2. Расчетное задание.

Электрические схемы замещения для заданного варианта. Расчетные формулы и результаты расчета.

6.3. Экспериментальная часть.

Электрические схемы опытов. Результаты измерений (табл.2.2, 2.3, 2.4).

6.4. Обработка результатов экспериментов.

Расчетные формулы и соотношения. Таблицы результатов расчетов (табл.2.2, 2.3, 2.4).

6.5. Выводы по работе

 

7. Контрольные вопросы.

 

1. Что называется, от чего зависит, в каких единицах измеряется электрическим сопротивлением?

2. Что называется электрической проводимостью?

3. Как читается закон Ома для участка цепи?

4. Как осуществляется последовательное, параллельное и смешанное соединение потребителей?

5. Как формулируется первый закон Кирхгофа?

6. Как формулируется второй закон Кирхгофа?

7. По каким действиям можно судить о работе электрического тока?

8. В каких единицах измеряется работа (энергия) электрического тока?

9. Что называется электрической мощностью, каким прибором она изме­ряется и в каких единицах?

10. Как определить мощность, не имея ваттметра?