Четырёхугольник называется пространственным, если его вершины не лежат в одной плоскости.

Тема: «Взаимное расположение двух прямых в пространстве. Угол между двумя прямыми».

Ознакомьтесь с видеоуроком по ссылке https://resh.edu.ru/subject/lesson/6133/main/272669/

Ознакомьтесь с §7,8, 9 стр.15-18

Ознакомьтесь с образцами решения задач (переписать в рабочую тетрадь)

№38. b

В С

 

 

 

 

А D

 

 

а

Дано: ABCD – ромб, а ||BD, b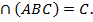

Доказать: а) а 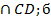) а и в –скрещивающиеся прямые.

Доказательство:

а)Так как а имеет с плоскостью (АВС) общую точку, то она либо лежит в этой плоскости, либо её пересекает. Пусть а пересекает плоскость (АВС), тогда параллельная ей прямая BD по лемме о пересечении плоскости параллельными прямыми также пересекает плоскость (АВС), что невозможно, так как BD лежит в ней по условию. Наше предположение не верно и прямая а не пересекает плоскость (АВС), а лежит в ней.

Мы учили, что если одна из двух параллельных прямых на плоскости пересекает третью прямую, то и вторая пересекает эту прямую. У нас а||BD, B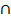D СD= .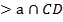

б) Мы доказали, что прямая а лежит в плоскости (АВС), а прямая в пересекает эту плоскость в точке С(по условию), не лежащей на этой прямой. Тогда а и в –скрещивающиеся прямые по признаку скрещивающихся прямых.

№39. Докажите, что если АВ и CD – скрещивающиеся прямые, то AD и ВС также скрещивающиеся прямые.

Дано: АВ и CD – скрещивающиеся прямые.

Доказать:AD и ВС- скрещивающиеся прямые.

 

 

D

А С

 

 

В

Доказательство.

Прямые в пространстве либо лежат в одной плоскости (пересекаются или параллельны), либо не лежат в одной плоскости(скрещивающиеся). Пусть прямые AD и ВС лежат в одной плоскости 𝛼, тогда точки А,В,С,D, лежащие на этих прямых попадают в одну плоскость 𝛼.

А 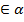,В 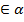, тогда прямая АВ лежит в 𝛼 по аксиоме .

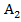D 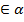,С 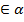, тогда прямая СD лежит в 𝛼 по аксиоме .

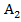Таким образом, прямые АВ и СD лежат в плоскости 𝛼, что противоречит условию задачи (прямые АВ и СD скрещивающиеся, т.е. не лежат в одной плоскости).

Значит, наше предположение не верное и прямые AD и ВС не могут лежать в одной плоскости, т. е. они скрещивающиеся.

№42.Даны параллелограмм ABCD и трапеция ABEK с основанием EK, не лежащие в одной плоскости. а) Выясните взаимное расположение прямых CD и EK. б) Найдите периметр трапеции, если известно, что в неё можно вписать окружность и АВ=22,5 см, ЕК=27,5 см.

С

 

D В

 

 

А E

 

 

K

 

Дано: параллелограмм ABCD и трапеция ABEK с основанием EK, не лежащие в одной плоскости, АВ=22,5 см, ЕК=27,5 см, окружность вписана ив трапецию.

Найти: взаимное расположение прямых CD и EK, .

Так как параллелограмм ABCD и трапеция ABEK, имеют две общие вершины Аи В, и по аксиоме 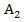прямая АВ лежит и в плоскости параллелограмма и в плоскости трапеции, то АВ это линия пересечения данных плоскостей и на рисунке отрезок АВ – общая сторона параллелограмма и трапеции.

По свойству параллелограмма DC||AB, по определения трапеции АВ||КЕ.

Известно, что если две прямые параллельны третьей прямой, то они параллельны.Тогда CD || EK.

Известно, что если в трапецию можно вписать окружность, то сумма её оснований равна сумме боковых сторон, т.е. АВ+КЕ=АК+ВЕ=22,5+27,5=50(см).

= АВ+КЕ+АК+ВЕ = 2 АВ+КЕ) =2 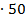=100(см).

Ответ: параллельны; 100см.

№43. Задача-теорема. Докажите, что середины сторон пространственного четырёхугольника являются вершинами параллелограмма (выучить формулировку наизусть, будет использоваться в дальнейшем при решении задач).

Четырёхугольник называется пространственным, если его вершины не лежат в одной плоскости.

Дано: пространственный четырёхугольник ABCD, точки Е,F, G,K - середины сторон АВ, ВС,СD,DA соответственно.

Доказать: ЕFGK - параллелограмм.

Доказательство:

В F С

 

E G

D

А

Чтобы представить себе пространственный четырёхугольник, представьте треугольную пирамиду. Макет вам демонстрировали в классе. Так вот вершины этой пирамиды и будут вершинами пространственного четырёхугольника.

Через три точки А,В,С, не лежащие на одной прямой по аксиоме 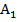проходит плоскость (АВС). Так как А и В лежат в этой плоскости, то по аксиоме прямая АВ лежит в этой плоскости, а значит и точка Е, лежащая на ней. Аналогично и точка F, лежит в плоскости (АВС). Точки Е и Fлежат в плоскости (АВС).Тогда по аксиоме прямая EF лежит в плоскости (АВС).

Е,F -середины сторон АВ и ВС ΔАВС, тогда ЕF - средняя линия ΔАВС. По теореме о средней линии треугольника ЕF||АС и ЕF= 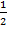АС.

Аналогично KG- средняя линия ΔАСDи по теореме о средней линии треугольника

KG ||АС и KG = 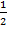АС.

ЕF||АС, KG ||АС= 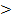ЕF|| KG,. Через две параллельные прямые ЕF и KG проходит плоскость по определению параллельных прямых. Точки Е,F, K,G, лежащие на этих прямых принадлежат этой плоскости, а следовательно и прямые ЕК и FG также принадлежат этой плоскости.

Так как ЕF= 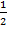АС, KG = 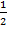АС, то ЕF= KG.

Имеем: ЕF= KG, ЕF|| KG.Тогда четырёхугольник ЕFGK - параллелограмм по признаку.

Домашнее задание

Выучить §7,8, 9 стр.15-18

Решить №37, №40,№41.