Интегрируя по y третье уравнение из уравнений (2.4), получим распределение скорости ω:
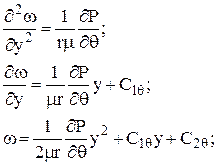
при y = 0 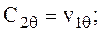
при y = h 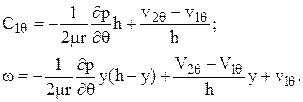 (2.7)
(2.7)
Для определения давления газа в каждой точке смазочного слоя к уравнениям движения необходимо добавить уравнение неразрывности, уравнение состояния и уравнение энергии. Уравнение неразрывности выражает постоянство массового расхода жидкости между двумя поверхностями подшипника.
В декартовой системе координат уравнение неразрывности можно записать в виде [80]

В цилиндрической системе координат уравнение неразрывности имеет вид

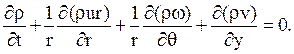 (2.8)
(2.8)
Это уравнение можно записать в интегральной форме. Умножим левую и правую части на dy и проинтегрируем в пределах от 0 до h:
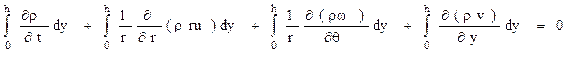

или
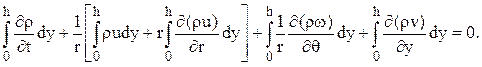 (2.9)
(2.9)
Известно, что
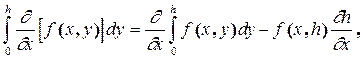 а
а
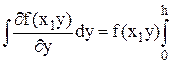 ,
,
поэтому уравнение (2.9) можно записать в виде
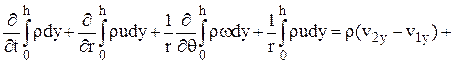 (2.10)
(2.10)
+ 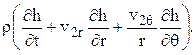
Уравнение состояния Клайперона-Менделеева определяет взаимосвязь между параметрами газа
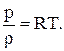 (2.11)
(2.11)
Изменение состояния газа в смазочном слое описывается уравнением политропного процесса 
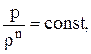 (2.12)
(2.12)
где n – показатель политропы.
Показатель политропы является переменным, но пределы его изменения довольно ограничены, лежат между адиабатой и изотермой  , что позволяет принимать некоторое среднее постоянное значение n.
, что позволяет принимать некоторое среднее постоянное значение n.
Уравнение энергии выражает зависимость между энергией частицы жидкости, механической работой внешних сил и напряжений и потоком тепла. Его можно получить из первого закона термодинамики и записать следующим образом:
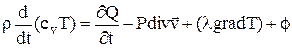
или

где 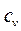 – изохорная теплоемкость,
– изохорная теплоемкость, 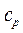 – изобарная;
– изобарная; 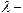 коэффициент теплопроводности;
коэффициент теплопроводности; 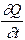 – тепло, выделяемое внутренним источником, например, химической реакцией;
– тепло, выделяемое внутренним источником, например, химической реакцией; 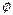 – диссипативная функция.
– диссипативная функция. 
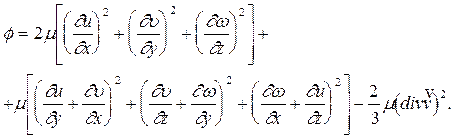
Если смазка осуществляется не реагирующими между собой газами, то ¶Q¤¶t=0.
В цилиндрических координатах уравнение энергии имеет вид
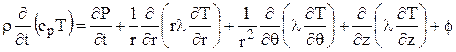 ,
,
где

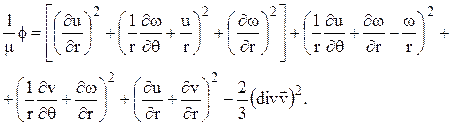
Из-за небольшой вязкости газов изменение температуры в смазочном слое незначительно. Многочисленные эксперименты показывают, что в подавляющем большинстве реальных подшипников течение газа в смазочном слое является практически изотермическим. Поэтому уравнение энергии и уравнение состояния можно заменить одним уравнением [80]
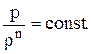 (2.12)
(2.12)
Таким образом, уравнения движения в смазочном слое (2.4), уравнение неразрывности (2.10) и уравнение (2.12) образуют систему четырех независимых уравнений с четырьмя неизвестными {u, w, P, r}.
Компонента n скорости в направлении оси y в эти уравнения не входит, если силами инерции пренебрегают.
Уравнение, содержащее в качестве неизвестной функции только давление, можно получить, если в уравнение неразрывности, записанное в интегральной форме (2.10) подставить зависимости (2.6), (2.7), полученные для распределения компонентов u и w скоростей в направлении осей r и q соответственно. При этом следует учесть, что r не зависит от y, так как p не зависит от y.
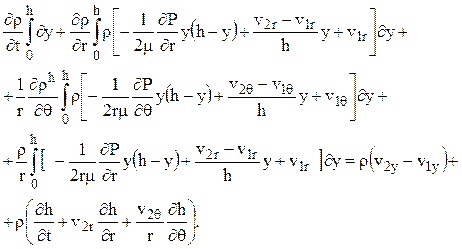 (2.13)
(2.13)
В этом уравнении
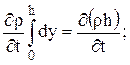
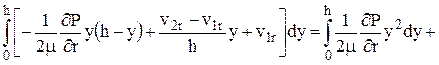

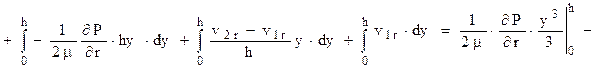

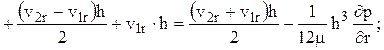

Поэтому уравнение (2.13) можно записать в виде
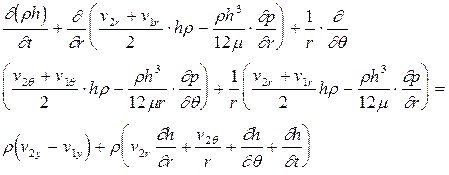
или
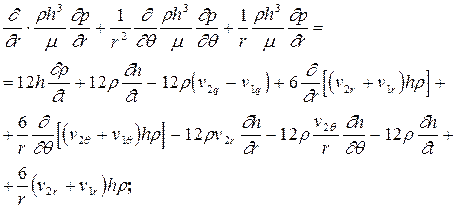
так как
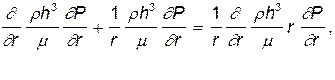
получим уравнение
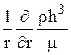 r
r 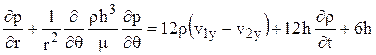
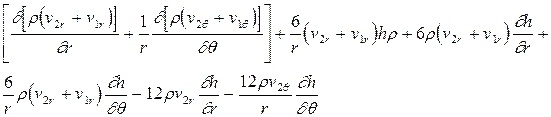

или
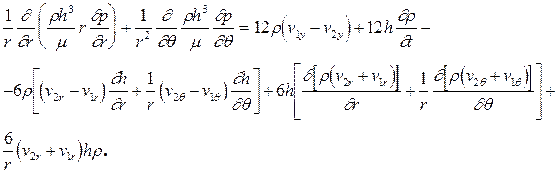
Исключив плотность при помощи уравнения политропы (r = P 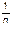 C, где C = const), получим дифференциальное уравнение, содержащее в качестве неизвестной функции только давление:
C, где C = const), получим дифференциальное уравнение, содержащее в качестве неизвестной функции только давление:
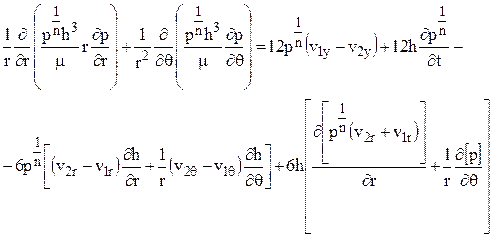
 . (2.14)
. (2.14)
В стационарных режимах в осевых подшипниках обычно
n1r = n2r = n1y = n2y =n2q = 0.
В стационарном режиме также 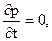 а n1q = wr, где w – угловая скорость цапфы. Поэтому уравнение (2.14) упрощается и приобретает вид
а n1q = wr, где w – угловая скорость цапфы. Поэтому уравнение (2.14) упрощается и приобретает вид

Так как температура в смазочном слое постоянная (процесс изотермический), вязкость газа не изменяется, получим следующее уравнение для распределения давления в смазочном слое осевого подшипника:
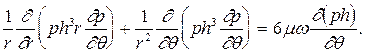 (2.15)
(2.15)
Если известны граничные условия для давления (обычно это давление на границах подшипника), геометрия смазочного слоя и подшипника, вязкость газа и скорость цапфы, то можно решить прямую задачу газовой смазки, определив при решении уравнения (2.15), как распределяется давление в смазочном слое подшипника.
При известном распределении давления определение интегральных характеристик подшипника (несущей способности, расхода газа на смазку, мощности трения и т.п.) не представляет особого труда.
Сложнее решение обратной задачи газовой смазки – определение геометрии смазочного слоя, при которой подшипник с учетом накладываемых ограничений имел бы наибольшую несущую способность или жесткость, наименьшее трение, наименьший расход газа на смазку и т.п. Простой перебор решений уравнения распределения давления для различных форм смазочного зазора довольно трудоемок. Для оптимизации формы смазочного слоя желательно использовать специальные методы оптимизации, опирающиеся на методы вариационного исчисления или теории оптимального управления.
На практике при проектировании подшипников обычно приходится одновременно определять геометрию смазочного слоя и всего подшипника, а также интегральные характеристики подшипника по заданным нагрузкам и параметрам газа, подаваемого на смазку.
2.2. Расчет осевых лепестковых газодинамических подшипников
Конструктивная схема осевого лепесткового газодинамического подшипника со взаимно перекрывающимися лепестками показана на рис. 2.2. Масштаб по толщине зазора лепестков существенно увеличен.
При общепринятых в теории газовой смазки допущениях уравнение распределения давления в смазочном слое осевого подшипника выведенное в параграфе 2.1, имеет вид
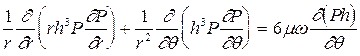 ,
,
где r – радиальная координата, q – угловая координата, h – толщина смазочного зазора, P – давление, m – динамическая вязкость газа, w – угловая скорость.
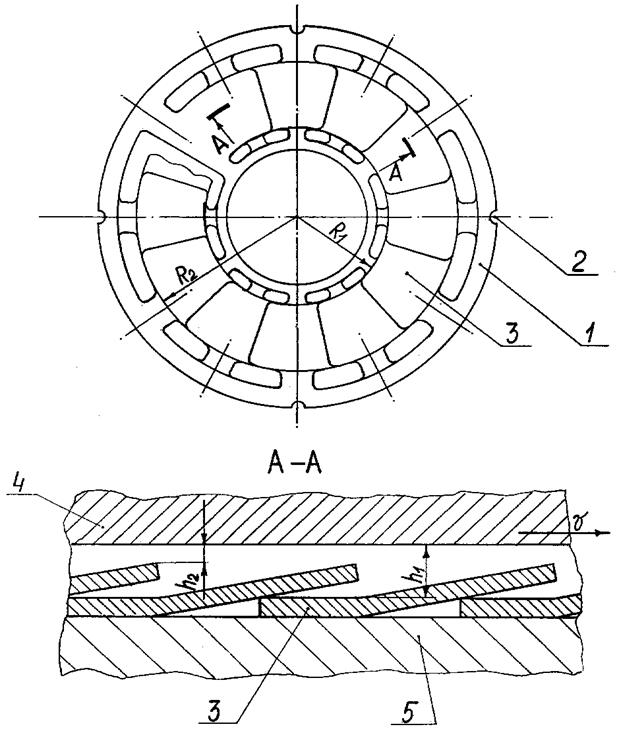
Рис. 2.2. Конструктивная схема осевого лепесткового газодинамического
подшипника:1– плата, 2 – паз установочный, 3 – лепесток, 4 – пята, 5 – корпус
Это уравнение можно записать следующим образом:
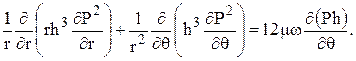 (2.16)
(2.16)
Если зазор в подшипнике изменяется и по углу и по радиусу, то уравнение (2.16) можно преобразовать к виду
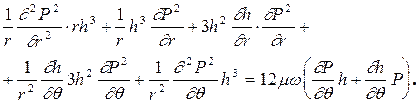 (2.17)
(2.17)
Произведем замену переменных в уравнении (2.17) и перейдем к уравнению (2.19) в безразмерном виде. При этом безразмерные величины будем записывать с чертой над символом:
 `P =
`P = 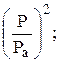 `h =
`h = 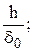
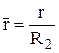 ,
,
где  – давление на краях подшипника; d0 – толщина лепестка; R2 – наибольший радиус подшипника.
– давление на краях подшипника; d0 – толщина лепестка; R2 – наибольший радиус подшипника.
Производные, входящие в уравнение (2.17), можно записать в виде
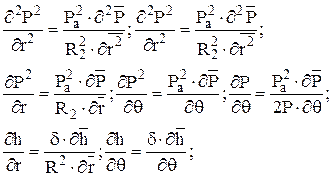 (2.18)
(2.18)
Уравнение в безразмерном виде
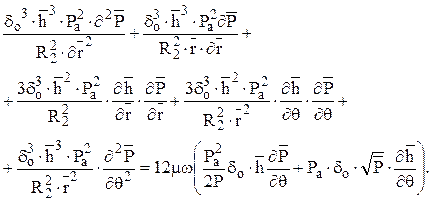 (2.19)
(2.19) 

Разделив все члены уравнения (2.19) на 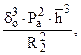 получим
получим
(2.20)
Производные, входящие в уравнение (2.20), аппроксимируем трехточечными центральными разностями

где i – номер линии сетки, проходящей по окружности; к – номер линии сетки, проходящей по радиусу.
Проведя алгебраические преобразования, получим систему конечноразностных уравнений распределения давления в смазочном слое подшипника
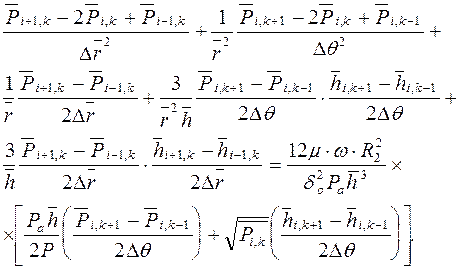
 (2.21)
(2.21)
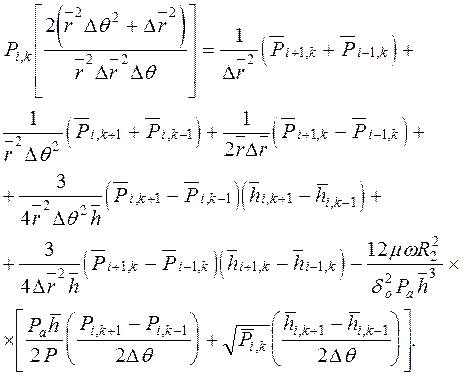 (2.22)
(2.22)
Разделив все члены уравнения (2.22) на 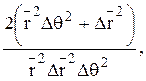 получим
получим
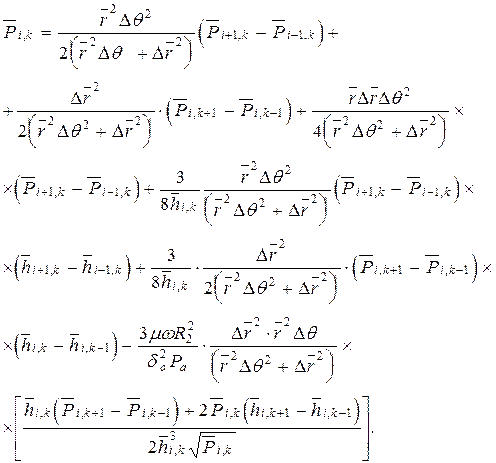 (2.23)
(2.23)
Для решения уравнения (2.23) необходимо знать граничные условия. Обычно это давление на краях подшипника. В безразмерной форме его можно выразить как
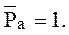 (2.24)
(2.24)
Решая систему конечно – разностных уравнений (2.23) последующими интеграциями методом Зейделя до удовлетворения граничным условиям (2.24), можно определить давление во всех узлах сетки.
При известном распределении давления можно вычислить интегральные характеристики подшипника: несущую способность, силу, момент и мощность трения, расход газа, жесткость.
Несущая способность равна
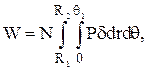
где N – количество лепестков в подшипнике, 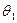 – угловая протяженность лепестка.
– угловая протяженность лепестка.
Несущая способность подшипника выраженная через безразмерные переменные
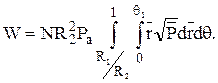
При численном интегрировании при известных давлениях в узлах сетки

Коэффициент несущей способности
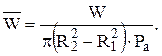
Коэффициент несущей способности, учитывающий давление окружающей среды, действующее на противоположную сторону пяты

Элементарный момент сил трения, действующий со стороны смазочного слоя на произвольный элемент площади типа rdrdq [144]
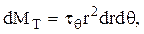

где tq – окружная составляющая касательного напряжения на рабочей поверхности шипа.
Согласно закону Ньютона о линейной связи между тензорами напряжений и скоростей деформации движущихся жидких и газовых объемов [101]

Касательные напряжения, а следовательно и моменты трения на шипе (y = 0) и на подшипнике (y = h) в общем случае не равны, так как производная  имеет различные значения на соответствующих поверхностях (см. формулу (2.7).
имеет различные значения на соответствующих поверхностях (см. формулу (2.7).
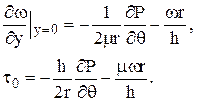
Момент сил трения, действующий со стороны смазочного слоя на шип в ЛГП
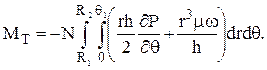
Мощность, затрачиваемая на преодоление сил трения
Nт = Mт w.
Если перейти к безразмерным переменным,
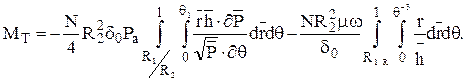



Переходя к конечным разностям получим,
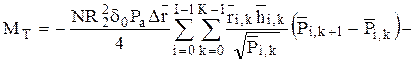
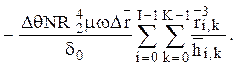
На несущую способность существенное влияние оказывает толщина смазочного зазора и его профиль. Газодинамические подшипники могут иметь значительную несущую способность, достаточную для многих быстроходных турбомашин, но при очень малых зазорах, порядка 10 мкм и меньше. Обеспечить на практике работоспособность машин с такими зазорами в подшипниках, применяя обычные подшипники скольжения с недеформируемыми втулками, очень сложно. Требуются высокая точность изготовления деталей, высокая чистота смазки, жесткие ограничения на температурные расширения.
Применение упругодеформируемых лепестков существенно облегчает задачу обеспечения работоспособности.
При проектировании подшипника весьма важно знать оптимальную форму профиля смазочного зазора и уметь выполнить эту форму, выбирая ту или иную конструкцию подшипника.
При отсутствии деформации лепестков профиль смазочного зазора в подшипнике (рис. 2.2) клиновидный. Зазор на линиях сетки будет определяться формулой
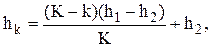 (2.25)
(2.25)
где K – количество интервалов сетки, проходящих по радиусу; k – номер линии сетки, k = 0 для первой линии, отсчитываемой по направлению скорости n (при h = h1); h1 – максимальный зазор (в начале лепестка); h2 – минимальный зазор.
В соответствии с рис.2.2
h1 = h2 + 2d0,
где d0 – толщина лепестка.
При достижении определенных давлений в смазочном слое лепесток начинает прогибаться и профиль смазочного зазора изменяться. Если лепесток прогибается, но пята при этом остается на месте, то
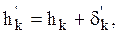
где dк¢ – прогиб лепестка.
Прогиб лепестка под действием сил давления в смазочном слое можно определить, используя законы теории упругости. Приближенно лепесток можно рассматривать как множество параллельных балок, равных числу линий сетки I, параллельных окружности.
На рис. 2.2 показан лепестковый газодинамический подшипник с перекрывающимися лепестками. При таком расположении лепестков возможны два варианта расчетных схем с шарнирной опорой в начале координат (рис. 2.3, а) и с жесткой заделкой начала лепестка(рис. 2.3, б).
Зная из решения уравнения (2.23) давления в узлах сетки
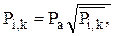
можно определить силы, действующие на лепесток в этих точках.
Так как с обратной стороны лепестка действует давление окружающей подшипник среды 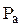 , то сила, действующая в узле сетки и деформирующая лепесток, может быть определена произведением избыточного давления на площадь элемента сетки.
, то сила, действующая в узле сетки и деформирующая лепесток, может быть определена произведением избыточного давления на площадь элемента сетки.
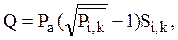
где 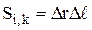 – площадь элемента сетки;
– площадь элемента сетки; 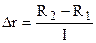 – шаг сетки по радиусу;
– шаг сетки по радиусу; 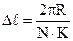 – шаг сетки по окружности; I – число интервалов сетки, проходящих по окружностям; K – число интервалов сетки, проходящих по радиусу; N – количество лепестков.
– шаг сетки по окружности; I – число интервалов сетки, проходящих по окружностям; K – число интервалов сетки, проходящих по радиусу; N – количество лепестков.
В дальнейших расчетах можно считать, что в узлах сетки действуют сосредоточенные силы Q.
Дифференциальное уравнение изогнутой оси балки
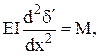 (2.26)
(2.26)
где E – модуль упругости материала лепестка; 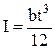 – момент инерции поперечного сечения (рис. 2.3, в); M – изгибающий момент.
– момент инерции поперечного сечения (рис. 2.3, в); M – изгибающий момент.
Проинтегрировав дважды уравнение (2.26) можно получить уравнение прогибов балки 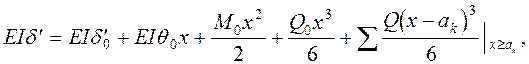 (2.27)
(2.27)
где d0' – прогиб в начале координат; q0 – угол поворота балки в начале координат; M0 – изгибающий момент в начале координат; Q0 – сила, действующая на балку в начале координат; Q – сила действующая на балку; а к – координата приложения силы.
Для расчетной схемы (рис. 2.3, а) можно найти реакции опор из уравнений статики
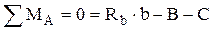 ,
,
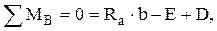 (2.28)
(2.28)
где B =  – сумма моментов сил давления на участке 1 от 0 до b, относительно точки А,
– сумма моментов сил давления на участке 1 от 0 до b, относительно точки А, 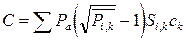 – сумма моментов сил давления на участке 11 от b до RӨ1
– сумма моментов сил давления на участке 11 от b до RӨ1 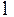 относительно точки А,
относительно точки А,
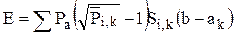 – сумма моментов сил давления на участке 1 от 0 до b относительно точки B,
– сумма моментов сил давления на участке 1 от 0 до b относительно точки B, 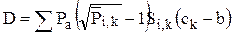 – сумма моментов сил давления на участке 11 от b до RӨ1 относительно точки В, а к – координата действия соответствующей сосредоточенной силы на участке 1 от 0 до b, ск – координата действия соответствующей сосредоточенной силы на участке 11 от b до RӨ1 (см. рис. 2.3, а).
– сумма моментов сил давления на участке 11 от b до RӨ1 относительно точки В, а к – координата действия соответствующей сосредоточенной силы на участке 1 от 0 до b, ск – координата действия соответствующей сосредоточенной силы на участке 11 от b до RӨ1 (см. рис. 2.3, а).
Из уравнений (2.28) Rb = (B + C) ¤ b; R  = (D – E) ¤ b.
= (D – E) ¤ b.
Уравнение прогибов балки 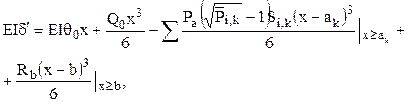 (2.29)
(2.29)
где Q0 = 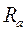 .
.
1 Rв 11q(x)
 Ra поперечное сечение
Ra поперечное сечение
балки
t
A
B
aк b
b
cк
Rq1 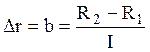
a) в)
1 Rв 11
Ra
A ак В
М0 b
ск
Rq1
б)
Рис. 2.3. Расчётные схемы лепестка
Угол поворота балки в начале координат q0 можно определить из условия, что при x = b, d' = 0. При этом первый и последний члены уравнения прогибов будут равны нулю
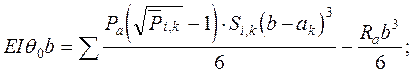 (2.30)
(2.30)
Для расчетной схемы (рис. 2.3, б) можно найти реакции опор из уравнений статики
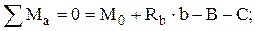 (2.31)
(2.31)
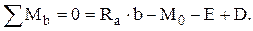 (2.32)
(2.32)
Уравнение прогибов, учитывая, что в защемлении q0=0,

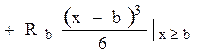 (2.33)
(2.33)
где Q0 = R 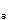 .
.
Так как при x = b, d' = 0 уравнение (2.33) можно записать
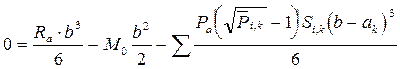 ,
,
отсюда
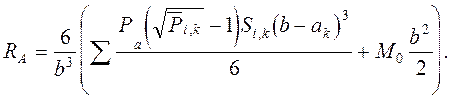
Подставляя значение Rа в уравнение (2.32), получим
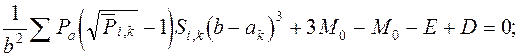
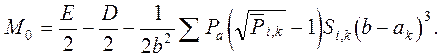
Из уравнения (2.31)

Уравнение прогибов
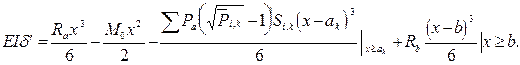 (2.34)
(2.34)
При достижении определенных давлений в смазочном слое лепесток начинает прогибаться и профиль зазора изменяться. В предельном случае, когда лепесток под действием сил давления полностью выжмется, смазочный слой можно рассматривать состоящим из двух участков. На первом по направлению скорости шипа участке зазор клиновидный, на втором – равномерный. Граница между участками проходит по линии сетки с номером K1.
Зазор на линиях сетки первого участка в этом случае можно определить по формуле
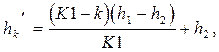
где h1 = d0 + h2 – зазор в начале участке, h2 – зазор в конце участка.
Зазор на линиях сетки с номерами k ³ K1
hк '' = h2 .
При проектировании ЛГП весьма важно знать оптимальную форму смазочного зазора, уметь выполнять эту форму, выбирая ту или иную конструкцию подшипника, а также уметь согласовывать между собой жёсткость смазочного слоя и жёсткость пакета лепестков.
На рис. 2.4 показана зависимость коэффициента несущей способности подшипника 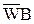 от параметра L = mwR22/d02 Pa при клиновидном смазочном зазоре и клиновидно-равномерном с границей между участками по середине лепестка. Для обоих подшипников несущая способность возрастает с увеличением параметра L. Увеличить параметр L наиболее просто за счет уменьшения толщины лепестка d0. Минимальное значение толщины лепестка определяется его прочностью. Лепесток должен безаварийно выдерживать действие сил сухого трения в момент пуска и остановки ротора.
от параметра L = mwR22/d02 Pa при клиновидном смазочном зазоре и клиновидно-равномерном с границей между участками по середине лепестка. Для обоих подшипников несущая способность возрастает с увеличением параметра L. Увеличить параметр L наиболее просто за счет уменьшения толщины лепестка d0. Минимальное значение толщины лепестка определяется его прочностью. Лепесток должен безаварийно выдерживать действие сил сухого трения в момент пуска и остановки ротора.
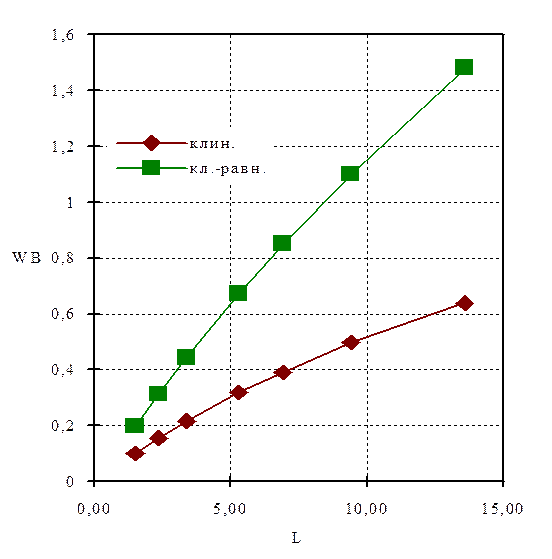
Рис. 2.4. Зависимость коэффициента несущей способности от параметра L: 
При переходе от клиновидного зазора к клиновидно-равномерному несущая способность подшипника увеличивается в 2 раза и более.
На рис. 2.5 показана зависимость коэффициента несущей способности лепестка с клиновидно – равномерным профилем смазочного зазора от расположения границы между участками. Явно выраженный максимум несущей способности наблюдается у подшипника с отношением длины клиновидного участка к длине всего лепестка равном 0,5.
Для обоих типов подшипников несущая способность возрастает с увеличением параметра L. Увеличить этот параметр наиболее просто за счет уменьшения толщины лепестка d0. Минимальное значение толщины лепестка определяется его прочностью. Лепесток должен безаварийно выдерживать действие сил сухого трения в момент пуска и остановки ротора.
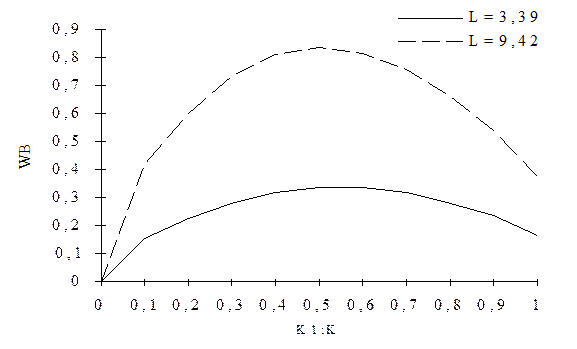 Рис. 2.5 Зависимость коэффициента несущей способности от
Рис. 2.5 Зависимость коэффициента несущей способности от
протяжённости клиновидного участка
Программа расчета осевых лепестковых подшипников с перекрывающимися лепестками с учетом прогиба лепестков, составленная на языке программирования СИ, представлена в приложении А. Блок-схема программы показана на рис. 2.6.
Распределение давления в смазочном слое подшипника, определённое по этой программе, представляется в виде, показанном на рис.2.7.
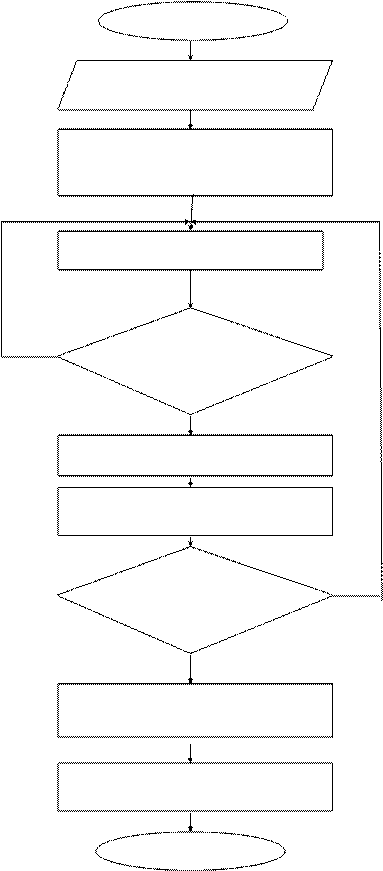 ПУСК
ПУСК
Ввод исходных параметров
Задание начальных значений
зазоров
Расчёт давления в узлах сетки
нет Проверка точности
определения давления
Расчёт прогибов лепестка
Определение новых зазоров