и
. (2.49)
Конечно, это справедливо только для теплоизолированного подшипника или, если температура газа, подаваемого на смазку, равна температуре окружающей среды.
Если произвести замену переменных и перейти к безразмерным величинам, то
. (2.50)
Приравнивая этот расход газа к расходу через питатель, также найденному для единицы длины кольцевого зазора, можно определить давление газа за питателями на входе в зазор. Для случая критического расхода газа
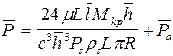
или
. (2.51)
После определения распределения давления в смазочном слое подшипника легко можно рассчитать интегральные характеристики опоры: несущую способность, жёсткость, момент и мощность трения, расход газа на смазку. Проекции главного вектора сил давления на линию центров и направление, перпендикулярное ей, в размерном виде можно определить по формулам
,
. (2.52)
Двойка перед интегралом учитывает то, что интегрирование происходит по 1/2 длины подшипника. Несущая способность подшипника
. (2.53)
В безразмерном виде, так как 
, а 
,
,
. (2.54)
Коэффициент несущей способности (удельная подъёмная сила на единицу площади проекции подшипника)
(2.55)
При численном интегрировании, если известно давление в узлах сетки, проекция главного вектора сил давления на линию центров равна сумме векторов сил давления сеточного прямоугольника
. (2.56)
Переходя к безразмерным переменным, получим 
(2.57)
Аналогично 
(2.58)
Угол положения линии центров
. (2.59)
Жёсткость смазочного слоя подшипника определяется как
(2.60)
Жёсткость, выраженная через безразмерные переменные
. (2.61)
Безразмерная жёсткость
. (2.62)
Таким образом, параметр жёсткости 
для определенной конструкции подшипника и заданных параметров наддува газа в смазочный слой равен наклону кривой, построенной в координатах 
в точке, равной заданному значению относительного эксцентриситета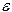 
. Следовательно, максимальная жёсткость опоры, которая часто является целью проектирования, может быть найдена по максимальному значению угла наклона.
Момент, создаваемый силами трения, действующий на элемент поверхности цапфы площадью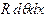 
[144],
. (2.63)
Окружная составляющая касательного напряжения
. (2.64)
Таким образом, если геометрия смазочного слоя, вязкость газа и угловая скорость цапфы заданы, то трение на её поверхности однозначно зависит от распределения давления в смазочном слое. Момент сил трения действующий со стороны смазочного слоя на цапфу
. (2.65)
Цифра 2 перед интегралом учитывает, что интегрирование производится только по 
длины подшипника.
Если перейти к безразмерным переменным
. (2.66)
При численном интегрировании, если известно давление в узлах сетки, а также учитывая, что в цилиндрическом подшипнике 
, 
.
Мощность, затрачиваемая на преодоление сил трения в подшипнике
. (2.67)
Суммарный массовый расход через сечение x = const в направлении оси подшипника составит [80]
. (2.68)
Так как после численного решения уравнения Рейнольдса известны значения давления в сеточных узлах области интегрирования приближенно расход удобно определить на ЭВМ суммированием расходов через прямоугольники, одна сторона которых равна 
, а другая – толщина смазочного слоя. Частную производную можно аппроксимировать по формуле
, (2.69)
а расход газа на подшипник выразить через
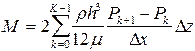. (2.70)
Если произвести замену переменных и перейти к безразмерным величинам, то
. (2.71)
Анализируя выраженные в безразмерной форме исходные уравнения (2.37) с граничными условиями (2.38) и (2.45),(2.46), можно сделать вывод, что для подшипников с надувом газа распределение давления в смазочном слое, а следовательно и интегральные характеристики, являются функцией нескольких безразмерных комплексов, т.е.
, (2.72)
где 
– число подшипника (параметр сжимаемости).
Если основные уравнения и граничные условия, полные и корректные, то полученные параметры образуют систему, необходимую и достаточную для моделирования [83]. Поэтому все результаты расчётов и экспериментов целесообразно представлять в зависимости от этих параметров. Так как уравнения отражают математическую модель явления, а не реальное явление, то они обладают некоторой степенью неопределенности и неточности. Слово "полные" означает, что все действительно важные физические явления отражены в математической модели. Окончательное утверждение о верности математической модели, а следовательно и о полученных комплексах подобия, можно сделать после экспериментальной проверки.
Программа расчёта интегральных характеристик двухрядных радиальных подшипников с наддувом газа на языке программирования Фортран представлена в приложении Б. Блок-схема программы показана на рис. 2.19
ПУСК
Ввод значений РS, RS,. ……
Резервирование памяти для массивов
нет
Проверка условия I=12
Проверка условия P/,K/> PK нет
Вычисление P/I, K/ по формуле (2,46)
Вычисление P/I, K/ по формуле (2,45)
Вычисление давлений в узлах сетки по формуле (2,43)
 | |||
|
Проверка P/I, K/-PI/I, K//<ε
Расчёт несущей способности, расхода газа
на смазку, момента, мощности трения
Вывод значений на печать
СТОП
Рис. 2.19. Блок-схема программы расчёта двухрядных цилиндрических
подшипников с наддувом газа
2.4. Расчёт осевых подшипников с наддувом газа
При расчёте упорных кольцевых подшипников с наддувом газа (рис. 2.20) уравнение Рейнольдса для газовой смазки можно записать в виде [80]
, (2.73)
где Р – давление в смазочном слое.
В цилиндрических координатах это уравнение имеет вид
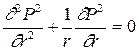. (2.74)
Граничными условиями будут давления:
на торцах подшипника при
(2.75)
а также в смазочном зазоре на кромках питателей, которые в начале расчёта обычно не известны.
 |
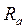
R1
R2
Ri
Рис. 2.20. Осевой подшипник
Сложность при решении состоит в том, что смазочный слой в рассматриваемом случае представляет собой многосвязную область. Поэтому при расчёте дискретные питатели, расположенные на одной окружности, заменяются эквивалентной им по расходу "линией наддува" [58, 61, 225]. При этом область интегрирования уравнения (2.74) становится трёхсвязной, т. е. при решении можно рассматривать три кольца с границами 
, 
и 
. Следовательно, если будут известны давления в смазочном слое на линиях наддува, для определения распределения давления в смазочном слое подшипника необходимо решить известную задачу Дирихле. Интегрируя уравнение (2.74), получим
, (2.76)
где С1 и С2 – постоянные интегрирования.
Рассмотрим первую область: 
; 
; 
;
; 
, (2.77)
где 
– давление на первой линии наддува.
Если перейти к относительным величинам
, 
, 
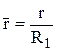, (2.78)
уравнение (2.77) можно записать в виде
. (2.79)
Вторая область: 
; 
; 
; 
; 
, (2.80)
где 
– давление на второй линии наддува.
В безразмерной форме
. (2.81)
Третья область: 
; 
;
; 
; 
. (2.82)
В безразмерной форме
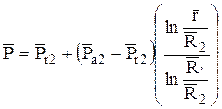. (2.83)
По уравнениям (2.79), (2.81), (2.83) можно найти распределение давления в смазочном слое подшипника, если будут известны граничные давления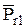 
, 
. Эти давления можно найти из условия баланса расходов газа через дискретные питатели в эквивалентную им «линию наддува» [ 225].
Критический расход газа через все питатели, расположенные на окружности можно определить по формуле изоэнтропийного истечения. При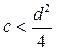 
, (2.84)
где ap – коэффициент расхода при истечении через питатель;
d – диаметр питателя;
с – зазор в подшипнике;
N – количество питателей;
rs – плотность газа, подаваемого на смазку.
Массовый расход при изоэнтропийном истечении газа через линию наддува, отнесённый к единице её длины рассчитывается по формулам
при 
при 
. (2.85)
Массовый расход газа через единицу ширины смазочного зазора при изотермическом потоке газа [80]
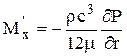, (2.86)
где m – динамическая вязкость газа.
При переходе к безразмерным величинам, учитывая равенство для изотермического процесса 
, получим
. (2.87)
Производные до и после линии наддува обозначим соответственно
и 
.
Уравнение баланса массовых расходов через единицу длины "линии наддува" и единицу ширины смазочных зазоров обоих областей имеет вид
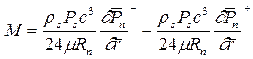, (2.88)
отсюда
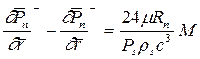. (2.89)
Поскольку на "линии наддува" производные имеют разрыв, аппроксимировать их можно по интерполяционной формуле Ньютона. Для перехода к конечно-разностным уравнениям выделим в окрестности питателей в обеих областях по две вспомогательные окружности с радиусами Rn-2, Rn-1, Rn+1, Rn+2, отличающимися друг от друга на D r, и производные выразим через конечные разности
, 
,
где Pn-2,`Pn-1,`Pn+1,`Pn+2 – безразмерные давления на радиусах Rn-2, Rn-1, Rn+1, Rn+2, соответственно.
Уравнение (2.89) приближённо заменяется уравнениями в конечных разностях
(2.90) при 
,
, (2.91)
при ,
где 
.
Определить`Pn можно решая совместно уравнения (2.79), (2.81), (2.83) и (2.90), (2.91) итерационным методом. После определения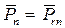 
по уравнениям (2.79), (2.81) и (2.83) находится распределение давления в смазочном слое подшипника. При известном распределении давлений не представляет труда определение интегральных характеристик подшипника: несущей способности, жёсткости, расхода газа на смазку, момента и мощности трения. Блок схема программы показана на рис. 2.21. Программы расчета на языках программирования Бейсик и Фортран представлены в приложении В и в приложении Г.
ПУСК
Ввод исходных данных
нет
Проверка условия I≤I1
Проверка условия I<I1 нет
Вычисление P/I/ по формуле (2,79)
 | |||
 | |||
Проверка условия P/I/>РК нет
Вычисление P/I/ по формуле (2,91)
Вычисление P/I/ по формуле (2,90)
 | |||
 |
Проверка условия I≤12 нет
| |||||
| |||||
| |||||
Проверка условия нет
I<12
Вычисление P/I/ по формуле (2,81)
Вычисление P/I/ по формуле (2,83)
нет
Проверка P/I -PI/I/<ε
Расчёт несущей способности, расход газа
на смазку, момента, мощности трения
Вывод значений на печать
СТОП
Рис. 2.21 Блок-схема программы расчёта осевых подшипников
с наддувом газа
2.5. Расчёт радиальных лепестковых газодинамических подшипников
Для определения основных интегральных характеристик (несущей способности, момента и мощности трения) радиального газодинамического подшипника необходимо решить дифференциальное уравнение
, (2.92)
где h – местная толщина смазочного слоя; P – давление газа в слое; m – динамическая вязкость газа; V – окружная скорость цапфы; x, z – декартовые координаты, ось x направлена по оси подшипника.
Поскольку в подшипниках с газовой смазкой температура газа в смазочном слое изменяется незначительно, можно считать m = const, а уравнение (2.92) записать в виде
. (2.93)
Это уравнение можно получить из уравнения (2.15) при переходе от цилиндрических координат к декартовым.
Если h = f(x, z), уравнение (2.93) можно записать как
или 
. (2.94)
При переходе к относительным координатам
; 
; 
; 
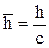, (2.95)
где Pa – давление на торцах подшипника, c – радиальный зазор в подшипнике при концентрическом положении шипа,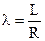 
– относительная длина подшипника, L – 1/2 длины подшипника, q – угловая координата, отсчитываемая от минимального зазора на линии центров в направлении вращения.
Производные, входящие в уравнение (2.94), можно записать следующим способом
; 
; 
; 
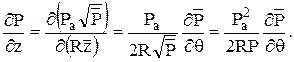(2.96)
Уравнение (2.94) в относительных координатах будут иметь вид
или
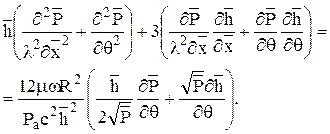(2. 97)
Результаты решения этого уравнения будут существенно зависеть от соотношения mw R2 ¤ Pa c2. В 1949 г. отечественный учёный С.А. Шейнберг [248, 249] предложил соотношение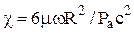 
называть числом подшипника и рассматривать его в качестве критерия подобия газовой смазки. В зарубежной литературе его часто называют числом сжимаемости подшипника, обозначая символом L. Производные, входящие в уравнение (2.97), аппроксимируем трехточечными центральным разностями
(2.98)
где 
– номер линии сетки, параллельной оси z; к – номер линии сетки, параллельной оси x.
Произведя ряд алгебраических преобразований можно получить эквивалентную уравнению (2.97) систему конечно-разностных уравнений
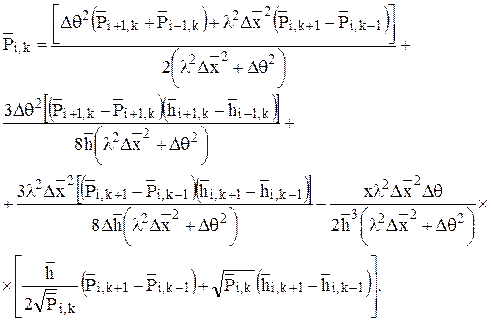(2.99)
Граничными условиями являются давления на торцах подшипника. Если давление одинаково и равно Pa, то в безразмерной форме его можно выразить как
(2.100)
Для того чтобы решить систему конечно-разностных уравнений (2.99) с граничными условиями (2.100), необходимо знать зазор между лепестком и цапфой в каждом узле сетки, что представляет достаточно сложную задачу для лепесткового подшипника.