Линейное программирование

Линейное программирование — это метод математического моделирования, разработанный для оптимизации использования ограниченных ресурсов. ЛП успешно применяется в военной области, индустрии, сельском хозяйстве, транспортной отрасли, экономике, системе здравоохранения и даже в социальных науках. Широкое использование этого метода также подкрепляется высокоэффективными компьютерными алгоритмами, реализующими данный метод. На алгоритмах линейного программирования базируются оптимизационные алгоритмы для других, более сложных типов моделей и задач исследования операций (ИО), включая целочисленное, нелинейное и стохастическое программирование.

Использование методов линейного программирования имеет ряд преимуществ перед традиционными методами:

1) если при использовании расчетно-конструктивных методов разрабатывается, как правило, один вариант решения и только в отдельных случаях несколько вариантов, то в линейном программировании принимаются во внимание все реально возможные варианты решений и из них выбирается наилучший, т.е. оптимальный;

2) схема расчетов решения задачи методами линейного программирования может быть формализована и автоматизирована для использования вычислительной техники, что обеспечивает экономию труда, ускоряет решение задачи и принятия управленческих решений;

3) использование современной вычислительной техники позволяет решить такие задачи, которые учитывают большое число факторов и условий производства, что значительно повышает качество и точность разрабатываемых вариантов развития социально-экономических процессов..

В самом общем виде задача линейного программирования математически записывается следующим образом:

(1)

где X = (x1, x2,..., xn); W – область допустимых значений переменных x1, x2,..., xn; f(Х) – целевая функция.

Для того чтобы решить задачу оптимизации, достаточно найти ее оптимальное решение, т. е. указать такое, что при любом .

Оптимизационная задача является неразрешимой, если она не имеет оптимального решения. В частности, задача максимизации будет неразрешимой, если целевая функция f(Х) не ограничена сверху на допустимом множестве W.

Методы решения оптимизационных задач зависят как от вида целевой функции f(Х), так и от строения допустимого множества W. Если целевая функция в задаче является функцией n переменных, то методы решения называют методами математического программирования.

Характерные черты задач линейного программирования следующие: показатель оптимальности f(X) представляет собой линейную функцию от элементов решения X = (x1, x2,..., xn); ограничительные условия, налагаемые на возможные решения, имеют вид линейных равенств или неравенств.

Задачей линейного программирования называется задача исследования операций, математическая модель которой имеет вид:

(2)
(3)
(4)
(5)

При этом система линейных уравнений (3) и неравенств (4), (5), определяющая допустимое множество решений задачи W, называется системой ограничений задачи линейного программирования, а линейная функция f(Х)называется целевой функцией или критерием оптимальности.

При описании реальной ситуации с помощью линейной модели следует проверять наличие у модели таких свойств, как пропорциональность и аддитивность.

Пропорциональность означает, что вклад каждой переменной в целевой функции и общий объем потребления соответствующих ресурсов должен быть прямо пропорционален величине этой переменной. Например, если, продавая j-й товар в общем случае по цене 100 рублей, фирма будет делать скидку при определенном уровне закупки до уровня цены 95 рублей, то будет отсутствовать прямая пропорциональность между доходом фирмы и величиной переменной xj. Т. е. в разных ситуациях одна единица j-го товара будет приносить разный доход.

Аддитивность означает, что целевая функция и ограничения должны представлять собой сумму вкладов от различных переменных. Примером нарушения аддитивности служит ситуация, когда увеличение сбыта одного из конкурирующих видов продукции, производимых одной фирмой, влияет на объем реализации другого.

Допустимое решение – это совокупность чисел (план) X = (x1, x2,..., xn), удовлетворяющих ограничениям задачи. Оптимальное решение – это план, при котором целевая функция принимает свое максимальное (минимальное) значение.

У линейных задачей, целевую функция f и функция g_i, которые линейны.

Общей задачей ЛП является задача нахождения max :

1. ∑a_ijx_j {<, =, >} b_i; i= j=
2. x_j≥0 j=

где a_ij, b_i, c_j – заданные постоянные, при этом целевая функция называется линейной формой.

Условие 1 – ограничение задачи

Условие 2 – условие неотрицательности переменных.

Стандартной (симметричной) задачей ЛП называется задача, в которой определяется экстремум целевой функции при выполнении условия 1 только в одну сторону и условия 2 для всех переменных.

Каноническая задача ЛП называется задача, в которой:

1. функция цели исследуется на максимум и минимум
2. ограничение задач только типа равенство
3. все переменные неотрицательны
4. все элементы правых частей положительны

Совокупность чисел, удовлетворяющих допущения задачи называется допущением решения или планом задачи.

План х^* при котором целевая функция достигает максимума, называется оптимальным => решение состоит в нахождении хотя бы одного оптимального плана.

Различные формы записи задачи ЛП:

1. векторная форма

=(x₁, …, x_n)

=(x₁, …, x_n)

Тогда векторная запись будет состоять в следующем:

Z=Cx→max

A₁x₁+…+A_nx_n<b x>0

1. матричная форма записи

Где А – матрица условий; Сх – скалярное произведение векторов; Ах – умножение матрицы на вектор.

Элементы выпуклого анализа.

Линейная комбинация векторов называется выпуклой, если выполняется условие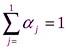

В двумерном случае линейная комбинация векторов есть отрезок, соединяющий эти точки.

Множество называется выпуклым, если вместе с каждой парой всех элементов оно содержит все их выпуклые комбинации.

Сглаживание линейных неравенств, образующих ОДЗ линейной задачи, определ. некоторое выпуклое множество, которое называется выпуклым многогранником решений.

Угловая точка многогранника решений – это точка, которая не является выпуклой комбинацией никаких других точек данного многогранника.

Если система ограничений содержи конечное число неравенств и имеется хотя бы одно допустимое решение, то угловых точек всегда конечно и не более чем число сочетаний из n элементов по m.

Угловые точки многогранника – вершины, а полуплоскости, проходящие хотя бы через 2 вершины называются гранями.

Вершины называются соседними, если существует грань их соединяющая.