МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН
КАЗАХСТАНСКО-НЕМЕЦКИЙ УНИВЕРСИТЕТ
Факультет экономических наук
Дисциплина: Математика в экономике
Утверждено
на заседании факультета ФЭН
от 1 февраля 2013 г. (протокол № 6)
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
По выполнению СРС
По теме «Комбинаторика»
для специальностей: 5В050900 – Финансы
5В051100 – Маркетинг
5В050700 – Менеджмент
Составитель: к.ф.-м.н. Кораблин А.Ю.
Алматы, 2013г.
СОДЕРЖАНИЕ
стр.
Указания……………………………………………………………………………...3
Комбинаторика. Предварительные сведения……………………………………...4
1. Перестановки……………………………………………………………………...6
2. Размещения………………………..........................................................................6
3. Сочетания……………………………………………………………………….....6
Решение типовых задач……………………………………………………………...8
Задачи для самостоятельного решения……………………………………….......11
УКАЗАНИЯ
Каждый студент самостоятельно должен решить дополнительные задачи по теме «Комбинаторика» в рамках изучения дисциплины «Математика в экономике». Для этого необходимо:
прочитать и разобрать следующие теоретические вопросы:
- перестановки
- размещения
- сочетания
При изучении перечисленных вопросов можно использовать, кроме данных методических рекомендаций, также любой учебник по математике, содержащий тему «Комбинаторика».
Задание на СРС включает дополнительные задачи №1-23 на стр. 11.
С целью самоконтроля к задачам приводятся ответы.
Задание на СРС выдается на занятии №21 (второй семестр).
Контроль СРС состоится на занятии №23 по расписанию занятий.
|
|
Контроль включает проверку решений указанных задач.
Оценка контроля СРС составляет максимально 2 балла.
Выполнение СРС является одним из условий допуска студента к экзамену по математике.
При выполнении СРС при необходимости можно получить консультацию у преподавателя по текущим вопросам в установленное время.
КОМБИНАТОРИКА
«Число, место и комбинация – три взаимно
перекрещивающиеся, но отличные сферы мышления,
к которым можно отнести все математические идеи»
Дж. Сильвестр [1]
В старинной задаче «Волк, козел и капуста» крестьянину нужно перевезти через реку волка, козла и капусту. Лодка так мала, что в ней кроме крестьянина может поместиться или только волк, или только козел, или только капуста. Но если оставить волка с козлом, то волк его съест, а если оставить козла с капустой, то будет съедена капуста. Как быть крестьянину?
Головоломки типа этой задачи называются комбинаторными. В таких головоломках требуется путем взаимной перестановки элементов расположить их в соответствии с условием задачи в определенном порядке.
В случае с крестьянином переправу нужно начать с перевозки козла. Затем крестьянин возвращается и берет волка, которого перевозит на другой берег и там оставляет, но везет обратно на первый берег козла. Здесь он оставляет его и перевозит к волку капусту. А затем, возвращаясь, перевозит козла.
К комбинаторным головоломкам относится и знаменитый кубик Рубика, и игры типа «Игра 15», а также головоломки с перестановкой шашек, «Ханойская башня» и др.
|
|
О Ханойской башне существует легенда, согласно которой где-то в глубине джунглей в буддийском храме находится пирамида, состоящая из 64 золотых дисков. День и ночь жрецы храма заняты разбором этой пирамиды. Они переносят золотые диски на новое место, строго соблюдая следующие правила: за один раз разрешается переносить только один диск и нельзя ни один диск класть на меньший диск. Предание гласит, что, как только жрецы закончат работу, грянет гром, храм рассыплется в пыль и наступит конец света.
Количество перемещений дисков, которые должны сделать жрецы, вычисляется по формуле 2n-1, где n – число дисков. Предположим, что жрецы
| работают так быстро, что за одну секунду переносят один диск. Тогда на всю работу им понадобится 264-1 с, или около 580 млрд. лет. За это время храм, действительно, может рассыпаться в пыль. | 
|
Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.
Выбором объектов и расположением их в том или ином порядке приходится заниматься чуть ли не во всех областях человеческой деятельности, например конструктору, разрабатывающему новую модель механизма, ученому-агроному, планирующему распределение сельскохозяйственных культур на нескольких полях, химику, изучающему строение органических молекул, имеющих данный атомный состав.
С аналогичными задачами, получившими название комбинаторных, люди столкнулись в глубокой древности. Уже несколько тысячелетий назад в Древнем Китае увлекались составлением магических квадратов, в которых заданные числа располагали так, что их сумма по всем горизонталям, вертикалям и главным диагоналям была одной и той же. В Древней Греции подсчитывали число различных комбинаций длинных и коротких слогов в стихотворных размерах, занимались теорией фигурных чисел (т.е. чисел, которые с помощью камешков можно представить в виде правильной фигуры), изучали фигуры, которые можно составить из частей особым образом разрезанного квадрата, и т.д.
|
|
Комбинаторные задачи возникали и в связи с такими играми, как шашки, шахматы, домино, карты, кости и т.д. (Например, задача о расстановке восьми ферзей на шахматной доске так, чтобы ни один из них не оказался под боем, об обходе всех полей доски шахматным конем и т.д.)
Комбинаторика становится наукой лишь в XVII в. – в период, когда возникла теория вероятностей. Чтобы решать теоретико-вероятностные задачи, нужно было уметь подсчитывать число различных комбинаций, подчиненных тем или иным условиям. После первых работ, выполненных в XVI в. итальянскими учеными Дж. Кардано, Н. Тартальей и Г. Галилеем, такие задачи изучали французские математики Б. Паскаль и П. Ферма. Первым рассматривал комбинаторику как самостоятельную ветвь науки немецкий философ и математик Г. Лейбниц, опубликовавший в 1666 г. работу «Об искусстве комбинаторики», в которой впервые появляется сам термин «комбинаторный». Замечательные достижения в области комбинаторики принадлежат Л. Эйлеру. Комбинаторными задачами интересовались и математики, занимавшиеся составлением и разгадыванием шифров, изучением древних письменностей. Теперь комбинаторика находит приложения во многих областях науки: в биологии, где она применяется для изучения состава белков и ДНК, в химии, механике сложных сооружений и т.д.
По мере развития комбинаторики выяснилось, что, несмотря на внешнее различие изучаемых ею вопросов, многие из них имеют одно и то же математическое содержание и сводятся к задачам о конечных множествах и их подмножествах. Постепенно выявилось несколько основных типов задач, к которым сводится большинство комбинаторных проблем.
Итак, комбинаторика занимается различного рода соединениями, которые можно образовать из элементов некоторого конечного множества. Термин «комбинаторика» происходит от латинского слова combina – сочетать, соединять.
Различают три основных вида соединений: перестановки, размещения и сочетания.
Перестановки
Перестановками называют соединения, которые можно составить из n предметов, меняя всеми возможными способами их порядок.
Число перестановок из n элементов обозначается символом Рn.
Число всех перестановок из n элементов равно произведению последовательных чисел от 1 до n включительно:
| Рn=1×2×3×…×(n-1)×n или | Рn=n! | (читается «n-факториал») |
Пример. Сколькими способами можно составить список из 10 человек?
Решение: Р10=10!=1×2×3×…×9×10=3628800 способов.
Размещения
Размещениями называют соединения, содержащие по m предметов из числа n данных, различающиеся либо порядком предметов, либо самими предметами.
Число размещений из n элементов по m обозначается символом 
и вычисляется по формуле:
=n(n-1)(n-2)…[n-(m-1)]
Замечание: Перестановки представляют частный случай размещений из n элементов по n в каждом, т.е. Рn= 
.
| Тогда = Рn / Рn-m или
| = 
|
Замечание: При решении задач часто используется равенство 
=(n-m)
Пример. Сколькими способами можно распределить 12 аудиторий под 12 учебных кабинетов?
Решение: 
=Р12=12!=479001600 способов.
Сочетания
Сочетаниями называют соединения, содержащие по m предметов из числа n данных, различающиеся друг от друга по крайней мере одним предметом.
Число сочетаний из n элементов по m обозначается символом 
и вычисляется по формуле:
| = / Рm или
| = 
|
Кроме того, при решении задач используются следующие формулы, выражающие основные свойства сочетаний:
1° = 
(0£m£n). По определению полагают 
=1 и 
=1
2° + 
= 
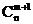Пример. Сколькими способами из 15 рабочих можно создать бригады по 5 человек в каждой?
Решение: 
= 
= 
= 
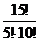=3003 способов.
Замечание: Еще во II в. до н.э. индийцы умели вычислять числа, которые мы обозначаем через , т.е. сочетания из n элементов, взятых по m, и знали формулу + 
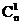+…+ =2n.
В Древней Индии, в Средней Азии и Китае было известно, что числа являются в то же время биномиальными коэффициентами[2]. Детальное изучение свойств биномиальных коэффициентов провел французский математик и философ Б. Паскаль в 1654 г.
Целый ряд комбинаторных задач возникает при разбиении множеств на части: найти, сколькими способами можно число n записать в виде суммы k слагаемых; найти, сколькими способами можно разложить n предметов по k ящикам, и т.д. Обычно задачи теории разбиений и раскладок сводятся к разобранным выше основным задачам комбинаторики.
Комбинаторика не сводится только к подсчету количества тех или иных подмножеств или последовательностей. При решении комбинаторных проблем иногда нужно лишь доказать, что данная проблема имеет решение, или убедиться в отсутствии его. Так, с помощью ЭВМ решена проблема четырех красок: доказано, что любую карту можно раскрасить в четыре цвета так, чтобы никакие две страны, имеющие общую границу, не были окрашены в один и тот же цвет.
В 1970-1980 гг. комбинаторика добилась новых успехов. Комбинаторные задачи физики, химии, биологии, экономики и других наук, которые не поддавались ранее решению из-за трудоемкости вычислений, стали успешно решаться на ЭВМ. В результате этого комбинаторные методы исследования все глубже проникают во многие разделы науки и техники.
Решение типовых задач по комбинаторике
Задача 1. Сколько различных перестановок можно образовать из букв слова «задача»?
Решение:
Если бы все шесть букв слова были различны, то число перестановок было бы равно 6!. Но буква «а» встречается в данном слове три раза, и перестановки только этих трех букв «а» не дают новых способов расположения букв. Поэтому число перестановок букв слова «задача» будет не 6!, а в 3! раз меньше, т.е.
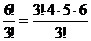=4∙5∙6=120
Задача 2. У богатого коллекционера было 10 ценных картин. Ему захотелось сделать одному музею подарок. Сколькими вариантами подарка располагает коллекционер: ведь подарить можно любую одну картину, любые две, любые три картины и т.д., можно даже подарить все десять картин?
Решение:
Число способов выбора одной картины из десяти определяется как число сочетаний из 10 элементов по 1, т.е. 
.
Число способов выбора любых двух картин из десяти определяется как число сочетаний из 10 элементов по 2, т.е.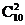 
и т.д.
Тогда число всевозможных способов выбора подарка равно:
+ + 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
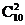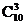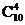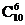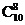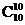
Поскольку + +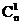…+ =2n, и, следовательно, 
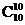+ +…+ =210, то
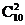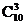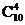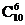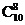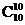+ + + + + + + + + =210- =210-1=1024-1=1023
Задача 3. На одной скамье занимают места два англичанина, два шотландца, два уэльсца, один француз, один итальянец, один испанец и один американец. Англичане не хотят сидеть рядом, шотландцы не хотят сидеть рядом и уэльсцы тоже не желают сидеть рядом друг с другом. Сколькими различными способами могут разместиться на скамье эти 10 человек так, чтобы никакие два человека одной и той же национальности не сидели рядом?
Решение:
Если нет никаких ограничений, то 10 человек можно рассадить 10!=3628800 способами. Сколько из этих перестановок запрещено? Будем рассматривать двух человек одной национальности, заключенных в скобки, как единое целое.
1. Тогда
(А, А) (Ш, Ш) (У, У) Ф Ит Ис Ам
можно переставить
7!∙(2!)3=40320 способами.
Помните, что два А могут меняться местами внутри скобок, где бы последние ни расположились, и то же самое верно для двух Ш и двух У. Отсюда и появляется (2!)3.
Итак, имеется 40320 способов, чтобы одновременно англичане сидели рядом, шотландцы сидели рядом и уэльсцы сидели рядом друг с другом.
2. Однако мы можем рассмотреть
(А, А) (Ш, Ш) У У Ф Ит Ис Ам,
где два У не объединены скобками, а расположены произвольно. Это даст нам
8!∙(2!)2=161280 вариантов,
но мы должны исключить отсюда результат пункта 1, чтобы не сосчитать некоторые перестановки дважды. Получаем
161280-40320=120960 способов,
чтобы англичане сидели рядом, шотландцы сидели рядом, но в то же время уэльсцы рядом не сидели.
3. Аналогично, рассмотрим
(А, А) Ш Ш (У, У) Ф Ит Ис Ам,
где два Ш не объединены скобками, а расположены произвольно.
Получим 120960 способов, когда англичане сидят рядом, уэльсцы сидят рядом, но в то же время шотландцы рядом не сидят.
4. Так же рассмотрим
А А (Ш, Ш) (У, У) Ф Ит Ис Ам,
где два А не объединены скобками, а расположены произвольно.
Получим 120960 способов, когда шотландцы сидят рядом, уэльсцы сидят рядом, но в то же время англичане рядом не сидят.
5. Но мы можем рассмотреть
(А, А) Ш Ш У У Ф Ит Ис Ам,
где и два Ш, и два У располагаются свободно. Это даст нам
9!∙(2!) =725760 случаев,
из которых мы должны вычесть результаты пунктов 1, 2 и 3, чтобы не сосчитать некоторые перестановки несколько раз. Получаем
725760-40320-120960-120960=443520 способов,
когда англичане сидят рядом, но при этом шотландцы рядом не сидят и уэльсцы рядом не сидят.
6. Аналогично, рассмотрим
А А (Ш, Ш) У У Ф Ит Ис Ам,
когда в скобки заключены только два Ш.
После вычитания результатов пунктов 1, 2 и 4 получим 443520 способов, когда шотландцы сидят рядом, но при этом англичане рядом не сидят и уэльсцы рядом не сидят.
7. Так же рассмотрим
А А Ш Ш (У, У) Ф Ит Ис Ам,
когда в скобки заключены только два У.
После вычитания результатов пунктов 1, 3 и 4 получим 443520 способов, когда уэльсцы сидят рядом, но при этом англичане рядом не сидят и шотландцы рядом не сидят.
Теперь из первоначального числа всевозможных перестановок 10! вычитаем результаты пунктов 1–7, т.е. перестановки, в которых хотя бы два человека одной национальности оказываются сидящими рядом, и получаем число перестановок, в которых никакие два человека одной национальности не будут сидеть рядом друг с другом:
3628800-40320-120960-120960-120960-443520-443520-443520=1895040