ОЦЕНКА НАИБОЛЕЕ ВЕРОЯТНЫХ ЗНАЧЕНИЙ ФИЗИЧЕСКИХ СВОЙСТВ
Вариант 7
Выполнили: студент гр. 2А080
Свитко П.С.
Рамазанов А.Ф.
Проверил: доцент
Устинова В. Н.
Томск, 2012
Цель работы: знакомство со способами статистической обработки данных массовых измерений и получение навыков в применении критериев согласия при обработке геофизических данных.
1.Основные теоретические сведения
При проектировании геофизических работ, оценке эффективности геофизических методов (например, по коэффициенту петрофизической контрастности), а также при интерпретации геофизических данных используют статистические параметры физических свойств, определенные по большому числу измерений на образцах горных пород.
На первом этапе обработка петрофизических данных заключается в вычислении ряда распределения значений измеренного параметра X и построении вариационной кривой (или гистограммы), для чего промежуток значений (Xmax - X min) делят на K интервалов по определенному правилу. При вычислении числа интервалов (классов группировки) K может быть использована эмпирическая формула К = 1 + 4 lgN[ 3 ], где N - общее число значений параметра в выборке (объем выборки). При небольших значениях N количество интервалов группирования можно определять в зависимости от объема выборки следующим образом (по В.М. Квятковскому):
Таблица 1
| Объем выборки N | <30 | 31 - 45 | 46 - 60 | 61 - 84 | 85 - 100 | 101 - 120 |
| Число интервалов К |
В этом случае длину интервала группирования определяют по формуле:
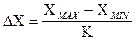 ,
,
Рассчитанное значение DC не должно быть менее двойной погрешности измерений параметра.
При больших объемах выборки длину интервала группирования можно определить по формуле Стерджеса:

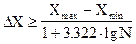 .
.
Например, имеем 27 значений измерения удельного электрического сопротивления образцов (в Ом м):
11, 32, 44, 25, 49, 13, 16, 22, 27, 36, 43, 16, 27, 21, 33, 25, 31, 37, 24, 32, 27, 38, 24, 35, 26, 18, 25. В соответствии с таблицей 1, при N = 27 выберем К = 4, тогда длина интервала группирования:
Dr = (rMAX - rMIN)/K = (49 - 11)/4 » 10 Ом м.
Для выяснения характера распределения сопротивлений построим вариационный ряд:
Таблица 2
| № п/п | Интервал группирования | Центр | Частота | Частость | |
| (r i) | (r i+1) | интервала | (n i) | Pi = ni / N | |
| 0.185 | |||||
| 0.408 | |||||
| 0.296 | |||||
| 0.111 |
å = 27 å = 1.0
В графическом виде ряд распределения может быть представлен, как полигон распределения, или как гистограмма распределения (рис. 1, 2). По вертикальной оси откладывают либо частоты n, либо частости Р. Плавная кривая, соединяющая средние точки ступеней гистограммы, называется вариационной кривой.
При достаточно больших выборках частости (Pi),будут приближаться к вероятностям попадания случайной величины в i-тый интервал (т.е. к плотностям вероятности), а вариационная кривая будет приближаться к закону распределения вероятностей измеренной величины (признака) Х.
Наиболее вероятные статистические характеристики физических свойств для массивов горных пород определяются в зависимости от закона распределения данного признака. Для петрофизических групп пород наиболее распространены два закона распределения - распределение Гаусса (нормальный закон распределения) и логарифмически нормальное распределение (логнормальный закон).
1.1. Нормальный закон распределения.
Нормальным (или гауссовым) называют распределение вероятностей непрерывной случайной величины, которое описывается функцией:
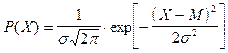 , (1)
, (1)
где M - математическое ожидание, s - среднее квадратическое отклонение (стандарт) случайной величины X.
Как это видно из формулы (1), нормальное распределение определяется двумя параметрами - M и s. При этом математическое ожидание (М), модальное значение (Mo) и медиана (Me) численно совпадают. В том случае, когда M = 0 и s = 1, нормальную кривую называют нормированной. При вычислении выборочных характеристик по вариационному ряду:
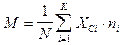 или
или 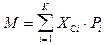 , (2)
, (2)
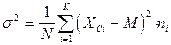 или
или 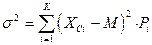 , (3)
, (3)
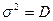 ,
, 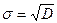 ,
,
где D - дисперсия случайной величины, 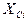 - значения случайной величины в центрах интервалов.
- значения случайной величины в центрах интервалов.
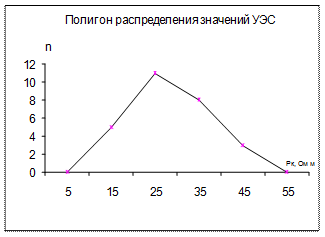 | 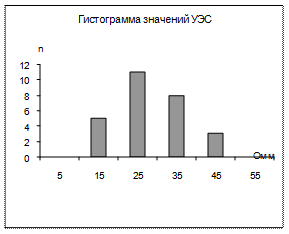 | ||
Рис. 1 Рис. 2
Например, для данных, приведенных в таблице 2:
M = (15 x 5 + 25 x 11 + 35 x 8 + 45 x 3) / 27 = 28,3 Ом м,
или M = (15 x 0.185 + 25 x 0.408 + 35 x 0.296 + 45 x 0.111) = 28.3 Ом м,
D = s2 = [(15-28.3)2 x 5 + (25-28.3)2 x 11 + (35-28.3)2 x 8 + (45-28.3)2 x 3] / 27 = 81.4 (Ом м)2 ,
или D = s2 = [(15-28.3)2 x 0,185 + (25-28.3)2 x 0,408 + (35-28.3)2 x 0,296 + (45-28.3)2 x 0,111] = =81.4 (Ом м)2 ,
s = 9,02 » 9 Ом м.
Стандарт характеризует изменчивость случайной величины в истинных значениях, тогда как дисперсия характеризует изменчивость квадратов значений.
1.2. Логнормальный закон распределения.
Значения случайной величины X считаются распределенными логарифмически нормально, если логарифмы этих значений распределены по нормальному (Гауссовскому) закону. То есть, логарифмически нормальный закон можно считать логарифмически преобразованным нормальным законом, поэтому функция плотности вероятности логарифмов аналогична нормальному закону распределения:
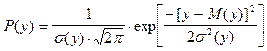 , (4)
, (4)
где 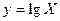 ,
, 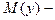 математическое ожидание величины
математическое ожидание величины 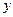 ,
, 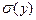 - стандарт величины
- стандарт величины 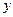 (логарифмический стандарт).
(логарифмический стандарт).
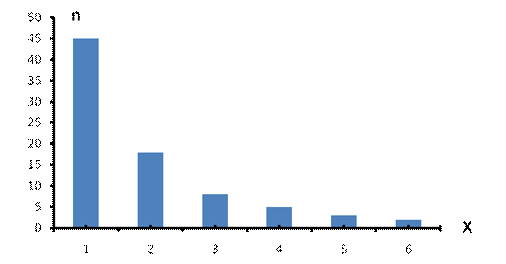
Рис. 3. Логнормальное распределение величины Х в линейном масштабе.
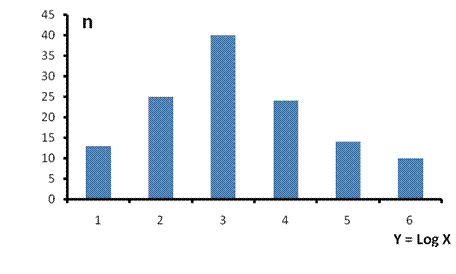
Рис. 4. Логнормальное распределение величины Х в логарифмическом масштабе.
Мода (Мо), медиана (Ме) и математическое ожидание (M) логнормально распределенной случайной величины X не равны между собой, а образуют неравенство Мо < Ме < М (рис. 3), тем более сильное, чем больше параметр 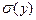 .
.
Логнормальное распределение симметризуется с помощью логарифмического масштаба по оси абсцисс или если вместо случайной величины Х оперировать ее логарифмом Y = lg X (рис. 4). В последнем случае для вычислений статистических характеристик величины Y можно использовать формулы (2) и (3). Для перехода к статистическим характеристикам величины X необходимо лишь вычислить антилогарифмы соответствующих величин Y:
M(X) = ant lg M(Y) и s(X) = ant lg s(Y)
Как показывает практика геофизических работ, нормальным распределением удовлетворительно описываются магнитные поля над слабомагнитными породами (осадочные породы, кислые эффузивы, слабометаморфизованные сланцы и др.), а также магнитные свойства этих пород; поля rК над проводящими геологическими образованиями; плотности большинства горных пород; сейсмические скорости; поляризуемость горных пород вне рудных интервалов и т.п.
Логнормальным законом обычно удовлетворительно описываются поля таких пород, для которых характерен широкий диапазон изменения физических свойств. К ним относятся магнитные поля и магнитные свойства основных и ультраосновных изверженных пород, значения rК для большинства комплексов пород, поляризуемость в пределах рудных интервалов сульфидно-полиметаллических месторождений и т. д.
1.3. Критерий согласия Пирсона.
В математической статистике гипотезу о принадлежности закона распределения к нормальному называют основной (нулевой) гипотезой. Статистическую проверку этой гипотезы по выборке производят при помощи критериев согласия. Такие критерии позволяют определить вероятность того, что при выполнении предполагаемого закона распределения наблюдающиеся в выборке отклонения от этого закона являются случайными, а не свидетельствуют об ошибочности гипотезы. Если такая вероятность велика, то отклонения от предполагаемого закона признаются случайными, а нулевая гипотеза о законе распределения не опровергается.
В исследовательской практике применяются самые различные критерии согласия, которые оформлены в виде государственных стандартов (напр., ГОСТ 11.006-74 “Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим”).
Проверка основной гипотезы с применением критериев согласия необходима чаще всего для обоснования возможности принятия тех или иных статистических решений. Наибольшее применение получили критерии согласия Колмогорова, Пирсона, Смирнова и др. Среди них наиболее общим, применяющимся для проверки не только нормального закона, но и других, является критерий Пирсона или критерий c2 (“хи - квадрат”).
В основе метода сравнения по критерию c2 лежит сравнение фактически наблюдаемых частот с теоретическими, которые вычисляются в предположении нормального распределения. Как правило, эти частоты отличаются друг от друга.
Теоретические частоты вычисляются с применением функции Лапласа (интеграла вероятности) Ф0(Z), где Z - нормированная переменная, определяемая по формуле:
Zi = (Xi - M) / s.
В этой формуле М - математическое ожидание, s - стандартное отклонение. Наименьшее значение Zi = Z1 получают равным - ¥, а наибольшее + ¥. Тогда теоретические вероятности попадания в i-тый интервал (теоретические частости) вычисляются по следующей формуле:
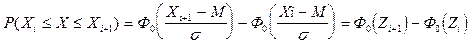 . (5)
. (5)
После того, как полученные значения теоретических вероятностей попадания умножим на объем выборки N, получим значения теоретических частот. Допустим, что в предположении нормального распределения генеральной совокупности вычислены теоретические частоты. При уровне значимости a требуется проверить нулевую гипотезу: генеральная совокупность распределена нормально. Уровень значимости a - это вероятность ошибочно отвергнуть нулевую гипотезу, когда она верна.
В качестве критерия для сравнения теоретических и фактических частот (а тем самым - проверки основной гипотезы) используют случайную величину:
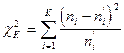 , (6)
, (6)
где через 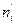 обозначены теоретические частоты попадания в интервал, а К - означает число интервалов. Случайной эта величина является вследствие случайности выборки и значений фактических частот
обозначены теоретические частоты попадания в интервал, а К - означает число интервалов. Случайной эта величина является вследствие случайности выборки и значений фактических частот 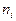 . Чем ближе друг к другу фактические и теоретические частоты для каждого интервала, тем меньше величина
. Чем ближе друг к другу фактические и теоретические частоты для каждого интервала, тем меньше величина 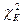 , а это служит признаком близости фактического и предполагаемого законов распределения.
, а это служит признаком близости фактического и предполагаемого законов распределения.
Правило проверки нулевой гипотезы следующее. Для того, чтобы при заданном уровне значимости проверить нулевую гипотезу Н0, надо вычислить теоретические частоты, а затем наблюдаемое значение критерия 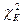 , и по таблице критических точек распределения
, и по таблице критических точек распределения 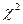 , (приложение 2) по заданному уровню значимости a и числу степеней свободы S найти критическую точку cКР2 (a; S). Если
, (приложение 2) по заданному уровню значимости a и числу степеней свободы S найти критическую точку cКР2 (a; S). Если 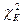 < cКР2 (a; S) - нет оснований отвергнуть нулевую гипотезу, если же
< cКР2 (a; S) - нет оснований отвергнуть нулевую гипотезу, если же 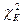 > cКР2 (a; S) - нулевую гипотезу отвергают.
> cКР2 (a; S) - нулевую гипотезу отвергают.
Уровень значимости чаще всего берут равным 0,05 (т.е. доверительная вероятность РДОВ =1- a = 0,95). Число степеней свободы находят по равенству S = K - 1 - r, где К - число интервалов выборки, r - число параметров предполагаемого распределения, которые оценены по данным выборки.
В нашем случае, для предполагаемого нормального распределения мы оцениваем два параметра - математическое ожидание М и стандарт s, поэтому r = 2 и число степеней свободы S = K - 3. При использовании критерия 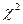 объем выборки должен быть достаточно велик, во всяком случае не менее 50. Каждый интервал частот должен содержать не менее 5 - 8 значений, малочисленные частоты объединяют, увеличивая для них интервал.
объем выборки должен быть достаточно велик, во всяком случае не менее 50. Каждый интервал частот должен содержать не менее 5 - 8 значений, малочисленные частоты объединяют, увеличивая для них интервал.
Поскольку возможны ошибки первого и второго рода, в особенности, если согласование теоретических и фактических частот “слишком хорошее”, следует проявлять осторожность. Например, можно увеличить число наблюдений, воспользоваться другими критериями, вычислить асимметрию и эксцесс и т. д.
2. Пример проверки основной гипотезы
по критерию Пирсона
Пусть мы имеем ряд измерений скоростей сейсмических волн. Объем выборки N = 150, VMAX = 3.81 км/с, VMIN = 3.18 км/с. При уровне значимости a = 0,05 требуется проверить нулевую гипотезу: генеральная совокупность распределена нормально. По формуле Стерджеса определяем количество интервалов К и длину интервала DV. В нашем случае К » 7 и DV » 0,1 км/с.
Порядок вычислений следующий.
1. Вычисляем математическое ожидание М и стандарт s по формулам:
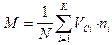 и
и 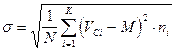 .
.
В нашем случае М = 3,50 км/с и s = 0,133 км/с (столбец 6 - для вычисления s).
2. Определяем нормированные по стандарту s переменные Z:
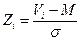 и
и 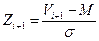 .
.
Поскольку нас интересуют теоретические частоты, а интервал их изменения ±¥, крайние значения переменной берем равными - ¥ и + ¥ (столбцы 7 и 8 табл. 3).
3. По таблице, приведенной в приложении 1 (см. в конце) определяем значения функции Лапласа от нормированных переменных 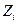 и
и 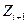 (столбцы 9 и 10).
(столбцы 9 и 10).
4. Затем определяем теоретические частости 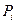 по формуле:
по формуле: 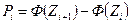 (столбец 11) Теоретические частоты ni определяем, умножая значения
(столбец 11) Теоретические частоты ni определяем, умножая значения 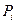 на объем выборки N (столбец 12). В нашем случае N = 150. При расчетах обычно делают проверку - сумма всех значений в столбце 11 должна быть равна 1, а в столбце 12 - величине N.
на объем выборки N (столбец 12). В нашем случае N = 150. При расчетах обычно делают проверку - сумма всех значений в столбце 11 должна быть равна 1, а в столбце 12 - величине N.
5. Вычисляем значения критерия Пирсона по семи интервалам (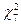 ). В столбце 13 табл. 3 приведены поинтервальные значения критерия, суммируя которые в соответствии с формулой (6), мы получаем искомую величину. В нашем случае
). В столбце 13 табл. 3 приведены поинтервальные значения критерия, суммируя которые в соответствии с формулой (6), мы получаем искомую величину. В нашем случае 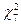 = 10,64.
= 10,64.
6. В соответствии с заданным уровнем значимости a и числом степеней свободы, по таблице критических точек распределения c2 (приложение 2 в конце) определяем 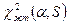 . Для нашего случая a = 0,05 и число степеней свободы S = K -3 = 4, поэтому
. Для нашего случая a = 0,05 и число степеней свободы S = K -3 = 4, поэтому 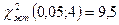 . Поскольку
. Поскольку 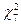 >
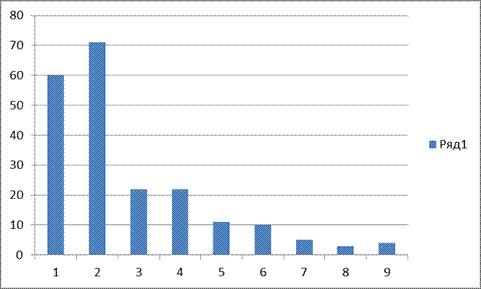
> 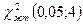 , нулевую гипотезу отвергаем.
, нулевую гипотезу отвергаем.
Обычно если мы предполагали, что закон распределения скорее всего нормальный, а нулевую гипотезу пришлось отвергнуть, полезен повторный анализ выборки для оценки того, все ли значения принадлежат данной выборке. Возможно, мы включили в выборку часть образцов, принадлежащих к другой группе. В рассматриваемом случае, при анализе графиков практических и теоретических частот (рис. 5), мы можем заключить, что закон распределения не относится к нормальному потому, что в выборке присутствуют две группы образцов с разными значениями М и довольно большими дисперсиями. Видимо, следует более тщательно рассмотреть образцы с учетом данных геохимических анализов и тогда, возможно, удастся разделить эти выборки.
3. Задание
Проверить нулевую гипотезу о принадлежности закона распределения к нормальному (или логнормальному) по критерию согласия Пирсона (c2) при уровне значимости a = 0,05. Сделать вывод о том, какие значения данного физического свойства необходимо использовать при создании физико-геологической модели. Исходные данные по вариантам приведены в приложении № 3 к лабораторной работе.
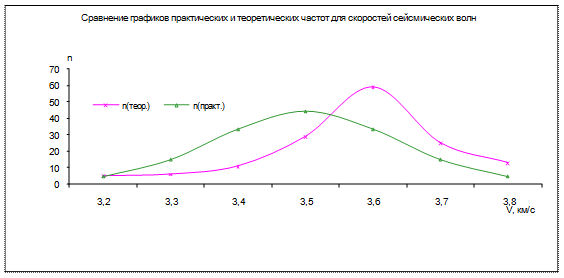 |
Рис. 5. Сравнение графиков практических и теоретических частот для скоростей сейсмических волн.
4. Ход работы:
Исходные данные:
| Вариант 5 | Удельные электрические сопротивления для песчаников | |||||||
| девона карагасской свиты в Ом м | ||||||||
| (Восточный Саян, Агульская площадь) | ||||||||
Рассчитываем по выше приведенным формулам и заполняем таблицу

| № | Интервалы | Центры их | Час-тоты | Расчет стандарта | Zi | Zi+1 | Ф(Zi) | Ф(Zi+1) | Теор. частости | Теор. частоты | Критич. знач. | |||
| i | Vi | Vi+1 | VCi | ni | (Vci-M)2×ni | Pi | ni | ci2 | M | Сигма | ||||
| 0,5 | 0,9 | 0,7 | 23,87506 | -1,38554 | -0,75402 | -0,4162 | -0,2734 | 0,1428 | 26,1324 | 12,86794 | 1,377596 | 0,633397 | ||
| 0,9 | 1,3 | 1,1 | 2,774136 | -0,75402 | -0,12251 | -0,2734 | -0,0478 | 0,2256 | 41,2848 | 0,775809 | ||||
| 1,3 | 1,7 | 1,5 | 0,779107 | -0,12251 | 0,509008 | -0,0478 | 0,195 | 0,2428 | 44,4324 | 1,101319 | ||||
| 1,7 | 2,1 | 1,9 | 5,731033 | 0,509008 | 1,140523 | 0,195 | 0,3729 | 0,1779 | 32,5557 | 6,358772 | ||||
| 2,1 | 2,5 | 2,3 | 10,20996 | 1,140523 | 1,772039 | 0,3729 | 0,4625 | 0,0896 | 16,3968 | 1,610988 | ||||
| 2,5 | 2,9 | 2,7 | 8,743767 | 1,772039 | 2,403554 | 0,4625 | 0,4918 | 0,0293 | 5,3619 | 0,026194 | ||||
| 2,9 | 3,3 | 3,1 | 5,933354 | 2,403554 | 3,035069 | 0,4918 | 0,49865 | 0,00685 | 1,25355 | 0,278594 | ||||
| 3,3 | 3,7 | 3,5 | 9,009201 | 3,035069 | 3,666584 | 0,49865 | 0,49984 | 0,00119 | 0,21777 | 1,588172 | ||||
| 3,7 | 4,1 | 3,9 | 6,362524 | 3,666584 | 4,2981 | 0,49984 | 0,499997 | 0,000157 | 0,028731 | 0,943363 | ||||
| 73,41814 | 25,55115 |
Строим графики
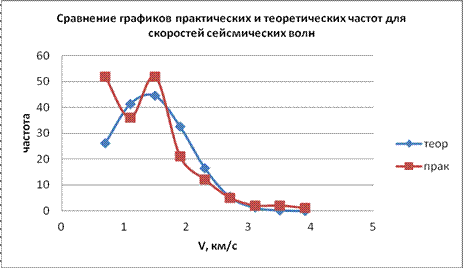
В соответствии с заданным уровнем значимости a=0,05 и числом степеней свободы, по таблице критических точек распределения c2 определяем c2экст. Для нашего случая a = 0,05 и число степеней свободы S = K -3 = 5, поэтому c2экст (0,05;6) = 12,6. Поскольку c2 >> c2экст, т.к. c2 =25,5 нулевую гипотезу отвергаем, по результатам наших расчётов закон близок к нормальному.
Вывод: познакомились со способами статистической обработки данных массовых измерений и получили навыки в применении критериев согласия при обработке геофизических данных.