Расчет коэффициентов ПФЭ при равном числе параллельных опытов в каждой точке факторного пространства
Коэффициенты находятся по формуле:
,
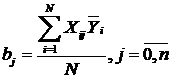где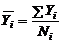 
- среднее значение параметра оптимизации, вычисленное по параллельным опытам 
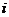– ой строки матрицы планирования 
.
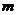Проверка значимости коэффициентов ПФЭ
Очевидно, что один фактор больше влияет на параметр оптимизации, другой – меньше. Поэтому можно проверить полученные коэффициенты регрессии на значимость, т.е. оценить величину влияния каждого фактора на значение параметра оптимизации. Если эта величина соизмерима с ошибкой эксперимента, то соответствующий коэффициент не несет дополнительной информации об объекте, и его можно приравнять к нулю, что упрощает математическую модель.
Значимость коэффициентов проверяется с помощью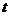 
– критерия Стьюдента.
Значения 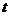– критерия вычисляются для каждого для каждого фактора по формуле:
, 
Полученные значения сравнивают с табличным значением критерия Стъюдента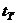 
, которое находится по числу степеней свободы 
, и уровню значимости α - величина, характеризующая вероятность того, что решение будет неправильным. Обычно принимают, что 
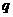α =0.05.
Если
> 
,
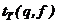то коэффициент значимо отличается от нуля, если же < 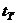, то коэффициент приравниваются к нулю: 
.
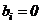В результате выполнения этого этапа моделирования получают уравнение регрессии, включающее значимые коэффициенты регрессии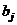 
.
Проверка адекватности линейного уравнения регрессии
Проверку адекватности уравнения регрессии проводят по 
- критерию Фишера. Суть этой проверки сводится к сравнению двух дисперсий: дисперсии адекватности 
и дисперсии воспроизводимости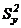 
. Если первая величина соизмерима со второй, то можно считать, это уравнение адекватно описывает экспериментальные данные. В противном случае оно не адекватно – тогда необходимо либо уменьшить интервал варьирования 
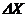, либо увеличить порядок уравнения регрессии.
Дисперсия адекватности определяется по формуле:
,
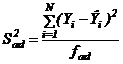где 
- расчетные значения, получаемые по уравнению регрессии,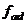 
- число степеней свободы 
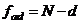, где 
- число значимых коэффициентов).
Затем вычисляют расчетное значение критерия Фишера ( - критерия):
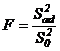
Расчетное значение критерия Фишера сравнивают с табличным значением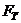 
, найденным при степенях свободы 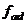и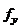 
, и заданном уровне значимости α. Если выполняется условие
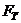> , (1)
то линейное уравнение регрессии признается адекватным. Если это условие не выполняется, т.е. < 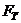, то уравнение считается неадекватным.
При расчете F предполагается что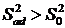 
. Если наблюдается обратное, то вывод об адекватности может быть сделан и без проверки условия (1).
Если модель адекватна, то ее можно использовать для поиска области оптимума объекта исследования или для предсказания отклика.
При неадекватной линейной модели наиболее часто принимают решение об уменьшении интервалов варьирования факторов и повторении эксперимента.
Итак, алгоритм расчета линейной модели с использованием ПФЭ следующий:
Задают матрицу планирования в кодированной форме для заданного числа факторов
Для каждого фактора задают базовую точку и интервал варьирования
Рассчитывают матрицу планирования в натуральной (размерной) форме
Проводят эксперименты, по матрице планирования, используя случайные числа.
Проводят серию опытов в центре плана, для определения ошибки опыта.
Вычисляют коэффициенты линейной модели
Проверяют коэффициенты на значимость
Проверяют модель на значимость
Выводы по проведенной работе.