Частные производные и дифференциал первого порядка

Тема 12. Частные производные и дифференциал функции многих переменных

 

Пусть имеется n +1 переменная x ₁, x ₂,..., x _n, y, которые связаны между собой так, что каждому набору числовых значений переменных x ₁, x ₂,..., x_n соответствует единственное значение переменной y. Тогда говорят, что задана функция f от n переменных. Число y, поставленное в соответствие набору x ₁, x ₂,..., x_n называется значением функции f в точке (x ₁, x ₂,..., x_n), что записывается в виде формулы y = f (x ₁ ,x ₂,..., x_n) или y =y (x ₁ ,x ₂,..., x_n).

Переменные x ₁, x ₂,..., x_n являются аргументами этой функции, а переменная y ‑ функцией от n переменных.

Далее будем говорить лишь о функции двух переменных. Для функций большего числа переменных все факты, о которых будет идти речь, или аналогичны или сохраняются без всякого изменения. Аргументы функции двух переменных будем обозначать как правило x и y, а значение функции  z.

Будем говорить, что задана функция двух переменных, если любой паре чисел (x,y) из некоторого множества D упорядоченных пар чисел поставлено в соответствие единственное число, которое обозначается f (x,y) и называется значением функции f в точке (x,y).

Множество D называется областью определения функции.

Поскольку любую пару чисел x,y можно рассматривать как пару координат точки M на плоскости, вместо z=f (x,y) можно писать z = f (M).При этом аргументами функции будут координаты x,y точки M.

Числа x, y можно рассматривать как координаты вектора , исходящего из начала координат и с концом в точке M (x,y). Тогда функция двух переменных будет функцией вектора, что записывается в виде формулы z = f (), причем аргументами функции являются координаты вектора .

График функции двух переменных есть множество точек (x, y, f (x, y)), где (x,y)Î D. График представляет собой некоторую поверхность. Пример такой

поверхности приводится на рисунке 1.

Пусть в плоскости XOY заданы две точки: M ₀(x ₀, y ₀) и M ₁(x ₁, y ₁). Расстояние r между этими точками рассчитывается по формуле

. (2)

Пусть d ‑ некоторое положительное число. d -окрестностью V_d точки M ₀(x ₀, y ₀) называется множество всех точек, координаты x,y которых удовлетворяют неравенствам

.

Очевидно, что d -окрестность точки M ₀(x ₀, y ₀) представляет собой круг радиуса d с выколотым центром.

Точка M ₀(x ₀, y ₀) называется точкой минимума функции z = f (x, y), если существует такое положительное число d, что из условия M (x, y) Î V_d (x ₀, y ₀) следует f (x, y) > f (x ₀, y ₀).

Точка M ₀(x ₀, y ₀) называется точкой максимума функции z = f (x, y), если существует такое положительное число d, что из условия M (x, y) Î V_d (x ₀, y ₀) следует: f (x, y) < f (x ₀, y ₀).

Точки минимума и максимума называются точками экстремума.

Число A называется пределом функции z = f (x, y) в точке M ₀(x ₀, y ₀):

,

если для произвольного числа e > 0 найдется такое число d > 0, что для всех точек M (x, y) из d -окрестности точки M ₀(x ₀, y ₀) выполняется неравенство

| f (x, y) - A |< e.

Функция z = f (x, y)называется непрерывной в точке M ₀(x ₀, y ₀), если

.

Два последних определения фактически повторяют определения предела и непрерывности в точке для функции одной переменной.

Частные производные и дифференциал первого порядка

 

Частной производной по переменной х функции в точке 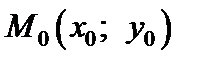называется предел

(1)

если он существует.

Производную (1) обозначают также

Частной производной по переменной у функции в точке называется предел

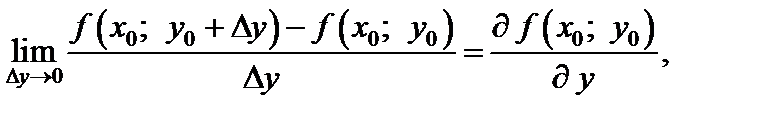(2)

если он существует.

Производную (2) обозначают также

Если частные производные определены на множестве и 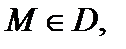то они являются функциями двух переменных

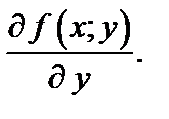
Для функции трех переменных в случае их существования, аналогично определяют три частные производные

Полным приращением функции в точке 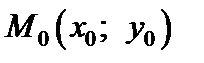называется разность где – приращения аргументов.

Функция называется дифференцируемой в точке если полное приращение функции в этой точке можно представить в виде

(3)

где А, В – некоторые числа; – бесконечно малые при

Если функция дифференцируема в точке М ₀, то в формуле (3)

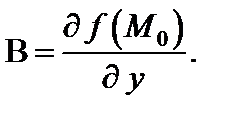
Главная часть полного приращения (формула (3)) дифференцируемой функции называется дифференциалом этой функции и обозначается dz:

(4)

Для независимых переменных х и у дифференциалы совпадают с их приращениями: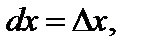

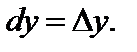
Дифференциал функции двух переменных вычисляется по формуле

(5)

Дифференциал функции трех переменных вычисляется по формуле

(6)

При достаточно малых и для функции , дифференцируемой в точке и ее окрестности, имеет место приближенное равенство

(7)

Для функции трех переменных (в случае дифференцируемости в точке М ₀ и малых приращениях независимых переменных) справедливо:

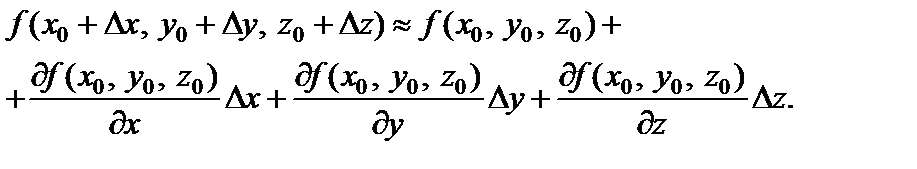(8)

 

Пример 1. Вычислить и функции

Найти значения частных производных в точке (–1, 1).

Решение. Зафиксируем у, вычислим производную по х, пользуясь правилами дифференцирования (условно считаем y = const):

 

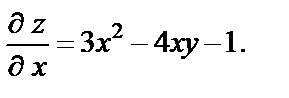
Тогда

Зафиксируем х, вычислим производную по у:

Тогда

 

Пример 2. Найти частные производные функции

Решение. Фиксируя у и z, вычислим производную по х:

Зафиксируем x и z и аналогично вычислим производную по y:

Зафиксируем x и y и вычислим производную по z:

 

Пример 3. Найти dz функции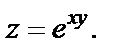

Решение. Используя формулу (18.5), найдем частные производные:

Тогда

 

Пример 4. Найти функции

Решение. Используя формулу (18.6), вычислим частные производные:

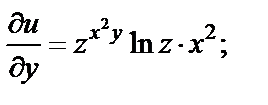
Тогда

Подставим

Получим:

 

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1. Дайте определение функции нескольких переменных.

2. Какая функция называется функцией двух переменных?

3. Что называется областью определения функции нескольких переменных?

4. Что называется частной производной функции двух переменных по одной из переменных?

5. Что называется полным приращением функции двух переменных?

6. Как определяется дифференциал функции двух переменных?

 

Домашнее задание: [1], ч.3, §18.1, 18.2, №1.1, 1.2