Пусть из нормально распределенной генеральной совокупности 
с неизвестным математическим ожиданием 
и известной дисперсией 
извлечена выборка 
объема 
. Выдвигается нулевая гипотеза 
о том, что значение математического ожидания генеральной совокупности равно числу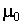 
:
.
Альтернативная гипотеза, область принятия нулевой гипотезы и критическая область выбираются, исходя из условий задачи (эксперимента). Возможны три варианта альтернативных гипотез:
, критическая область – двусторонняя;
, критическая область – левосторонняя;
, критическая область – правосторонняя.
Для проверки нулевой гипотезы используется случайная величина
,
где 
– выборочное среднее; 
– среднеквадратическое отклонение генеральной совокупности.
Если нулевая гипотеза верна, то случайная величина 
имеет стандартное нормальное распределение ( 
). Критическое значение статистики определяется исходя из вида альтернативной гипотезы:
для 
: 
или 
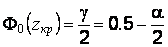, где 
– функция стандартного нормального распределения; 
– функция Лапласа (прил. 2);
для 
: 
или 
;
для 
: 
или 
.
Критическое значение статистики является квантилью нормированного нормального распределения, поэтому в дальнейшем будет использоваться обозначение 
или 
.
Эта же статистика используется в случае, когда дисперсия генеральной совокупности неизвестна, но объем выборки достаточно велик, 
. Тогда вместо в формулу подставляется значение оценки среднего квадратического отклонения 
, найденной по выборке.
Пример 4.1. На станке-автомате должны изготовляться детали с номинальным контролируемым размером 
мм. Известно, что распределение контролируемого размера является нормальным. Были измерены размеры 36 случайно отобранных деталей. Среднее значение контролируемого размера оказалось равным 
мм, выборочное среднее квадратическое отклонение оказалось равным 0,5 мм. Можно ли считать, что станок-автомат изготовляет детали уменьшенного размера и, следовательно, требует наладки?
Решение. По условию задачи необходимо проверить нулевую гипотезу о значении математического ожидания генеральной совокупности: 
мм против альтернативной 
(станок изготавливает уменьшенные детали). Критическая область – левосторонняя. Поскольку объем выборки достаточно большой ( 
), то вместо истинного значения СКО можно использовать его оценку 
мм.
Если нулевая гипотеза верна, то значения случайной величины
не должны сильно отличаться от нуля. Если же верна альтернативная гипотеза , то значение 
следует ожидать меньшим 12, соответственно значения должны быть значительно меньше нуля.
Положим уровень значимости 
равным 0,05. По определению критической области 
. Если гипотеза 
справедлива, то 
( 
– функция стандартного нормального распределения; 
– функция Лапласа). Тогда
.
Найдем экспериментальное значение статистики :
.
Экспериментальное значение критерия попало в критическую область 
, поэтому нулевую гипотезу следует отклонить в пользу альтернативной, станок нуждается в наладке.