ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №6
1. Вывод формулы для нахождения корней уравнения 𝑠𝑖𝑛𝑥 = 𝑎.
2. Определение окружности. Вывод уравнения окружности на плоскости. Приведение уравнения
+ 
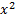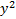+ 𝑎𝑥 + 𝑏𝑦 + 𝑐 = 0 к стандартному виду уравнения окружности.
1. Построим графики функций у = sin x и у = а.
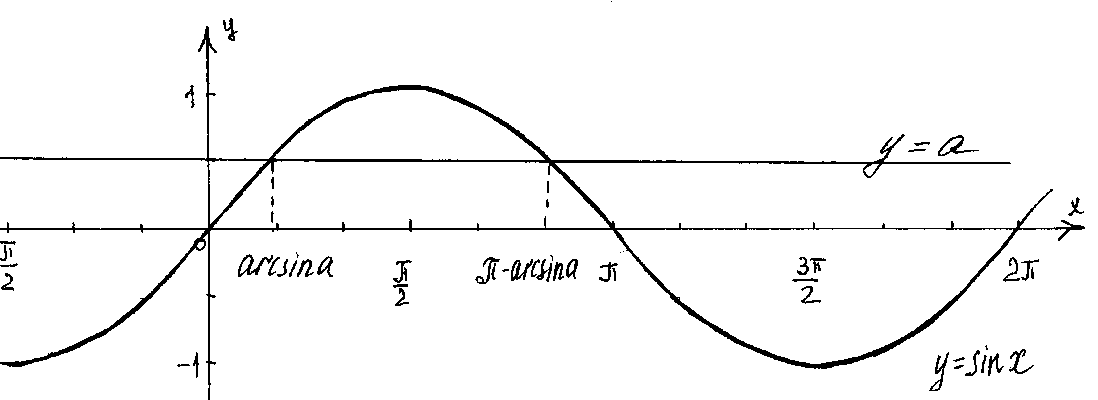
Если а> 1 и а < -1, то уравнение sin х = а не имеет решений, так как прямая и синусоида не имеют общих точек.
Если -1< а < 1, то по рисунку видно, что прямая у=а пересечет синусоиду бесконечно много раз. Это означает, что уравнение sin x = a имеет бесконечно много решений.
Так как период синуса равен 2π, то для решения уравнения sin x = a достаточно найти все решения на любом отрезке длины 2π.
Решением уравнения на [-π/2; π/2] по определению арксинуса х = arcsin a, а на [π/2; 3π/2] х = -arcsin a. Учитывая периодичность функции у = sin x получим следующие выражения:
, n 
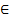Z.
Обе серии решений можно объединить:
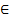, k Z.
Для каждого целого числа, подставленного вместо буквы n, каждая формула вычисляет соответствующий ему угол. Подставляя в n все целые значения, можно вычислить все множество углов (корней уравнения).
Понятно, что если вместо коэффициента «единица» перед арксинусом в формуле (4) поставить степень 
, то это не изменит результата при вычислении каждого угла, поскольку 2n – четно. В (5) формуле переставляем слагаемое π в конец выражения и выносим его за скобку. Это тождественное преобразование, также не меняющее результата при любом n. Затем вместо коэффициента -1 перед вторым арксинусом вставляем степень 
. И в этом случае результат сохранится, ибо при любом целом n значение 2n+1 будет нечетным, а при возведении 2n+1 в нечетную степень получим ту же самую «минус единицу».
В итоге формулы выглядят таким образом:
Докажем, что каждый угол, вычисляемый по (4) формуле, можно вычислить по формуле (6). В формулу (4) вставилось какое-нибудь целое число, например, n=7. Тогда в зеленой рамке получится 14. Если вставить 14 вместо переменной k в формулу (6), то получим те же действия, что и в (4) и, следовательно, совпадут результаты. Очевидность этого совпадения обеспечивает максимально близкий вид 4-ой формулы к 6-ой. Поэтому ни один угол формулы (4) не будет потерян. Аналогично с формулой (5). Итак, все углы формул (4) и (5) можно вычислить по формуле (6).
2.
Окружность – это замкнутая линия, все точки которой находятся на одинаковом расстоянии от данной точки. Эта точка называется центром окружности.
Радиус – отрезок, соединяющий центр окружности с точкой на окружности.
Диаметр – отрезок, соединяющий две точки окружности и проходящий через центр окружности.
Хорда – отрезок, соединяющий две точки окружности.
Вывод уравнения окружности на плоскости.
Выведем уравнение окружности радиуса r с центром С в заданной прямоугольной системе координат. Пусть точка С имеет координаты (хо; уо)
Расстояние от произвольной точки М (х; у) до точки С (хо; уо) вычисляется по формуле MC = 
Если точка М лежит на окружности, то МС = r, или 
, то есть координаты точки М удовлетворяют уравнению
(1)
Если точка М (х; у) не лежит на данной окружности, то 
, и координаты точки М не удовлетворяют уравнению (1).
Следовательно, прямоугольной системе координат уравнение окружности радиуса r с центром в точке С (хо; уо) имеет вид
.
Путём выделения полных квадратов уравнение 
+ 
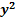+ 𝑎𝑥 + 𝑏𝑦 + 𝑐 = 0 можно привести к стандартной форме:
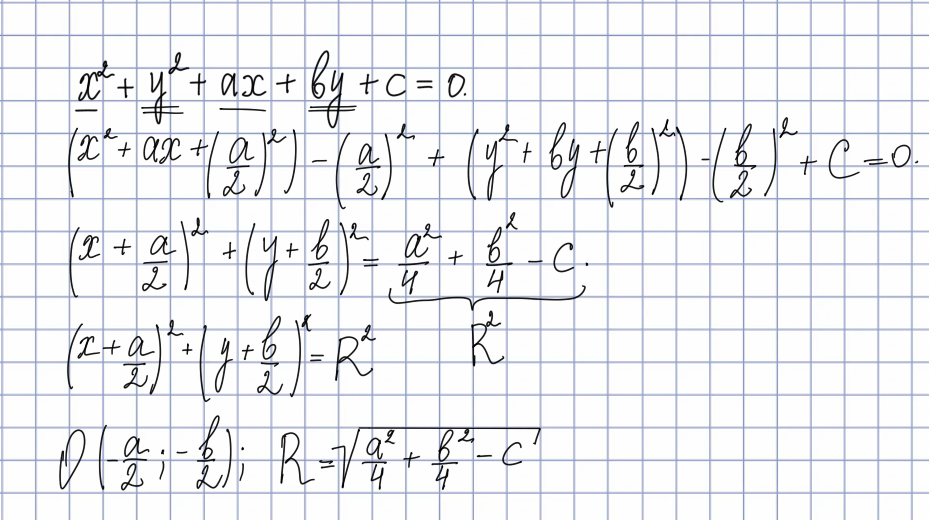
Практика.
