Для доказательства истинности некоторого утверждения А (n) при всех значениях натуральной переменной n, от которой оно зависит (начиная с n 0, n 0 Î N), часто используют метод математической индукции. Для этого необходимо сделать следующие три шага:
1. Проверить справедливость этого утверждения для n=1, т.е устанавливается истинность высказывания А(1). Эту часть доказательства называют базисом индукции.
2. Предполагается справедливость этого утверждения для n=k (предположение индукции).
3. Затем следует часть доказательства, называемая индукционным шагом. Доказывается справедливость этого утверждения для n=k+1 c учетом предполагаемой справедливости его для n=k, после чего делается вывод, что утверждение справедливо для любого натурального числа n, т.е. доказывают, что А(k) 
А(k+1).
Пример: Доказать справедливость формулы
(1.1)
для любого n Î N.
Решение. Используем метод математической индукции.
1. Проверяем справедливость равенства (1.1) при n =1. Для этого в равенстве (1.1) полагаем n =1, причем левая часть равенства будет состоять из одного слагаемого:
1 = 1 – выполняется.
2. Допускаем,что для n = k верно утверждение
(1.2)
3. Доказываем его истинность для n = k + 1:
Рассмотрим левую часть равенства (1.1):
Используем далее тот факт, что выражение в последних скобках, согласно (1.3), равно 
В итоге получаем
Правая часть равенства (1.1) для n = k + 1 имеет вид: 
Очевидно, что левая и правая части равенства (1.2) при n = k + 1 равны.
Так как все три шага математической индукции реализованы, формула верна для любого n Î N.
Знаки общности и существования
Знак общности 
(all – A) заменяет слова «все», «всякий», «каждый», «любой».
Знак существования 
(exist – E) заменяется в словесных формулировках словами «существует», «найдется», «какой-нибудь», «хотя бы один».
Если P(x) – некоторое неопределенное высказывание, заданное на множестве М, то запись 
означает: для любого элемента х из множества М имеет место P(x).
КОНТРОЛЬНЫЕ ВОПРОСЫ:
1. Приведите примеры высказываний (истинных и ложных), которые можно записать одними только знаками, без слов.
2. Прочтите словами следующие высказывания, записанные знаками; какие из этих высказываний истинны, а какие ложны:
; 
; 
; 
; 
?
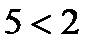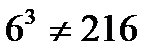4. Сформулируйте отрицания следующих высказываний:
,
,
,
.
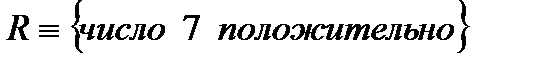Для каждого из высказываний укажите, что является истинным: само высказывание или его отрицание.
5. Для каждого из следующих высказываний составьте отрицание, а затем двойное отрицание. Убедитесь, что двойное отрицание совпадает по смыслу с исходным высказыванием:
,
,
.
6. На множестве М, состоящем из чисел 1,2,…,10, задано неопределенное высказывание 
.
Составьте таблицы истинности неопределенных высказываний 
и 
.
7. На множестве N, состоящем из чисел 1,2,…,10, задано неопределенное высказывание:
.
Укажите все пары 
элементов множества N, для которых высказывание 
истинно. Имеются ли такие пары , для которых одно из высказываний , 
истинно, а другое ложно? Имеются ли такие пары , для которых оба высказывания , 
истинны? Имеются ли такие пары , для которых оба высказывания , ложны?
8. Запишите с помощью знаков 
следующие высказывания:
a. Каково бы ни было натуральное число х, найдется также такое натуральное число y, что 
- простое число;
b. Каково бы ни было натуральное число х, можно подобрать такое натуральное число y, что 
;
c. Каково бы ни было натуральное число y, среди натуральных чисел найдется такое число х, что 
- четное число.
Домашнее задание: [1] ч.1, §1.1, №1.1, 1.3, §1.3, №1.1-1.3