Расчет характеристик резисторов

РЕЗИСТОРЫ

Резисторы – это компоненты РЭС, предназначенные для пе­ре­­рас­пре­деления и регулирования электрической энергии меж­ду эле­мен­тами электрической схемы.

Вопросы для самопроверки

1. Объясните принцип действия резистора.

2. Выполните классификацию резисторов по различным признакам.

3. Объясните систему обозначений резисторов в конструкторской документации. Расшифруйте пример записи резистора в констру­кторских документах:

С2-10-0,125 9880 Ом 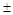0,5 % А ОЖ0.467.503 ТУ;

СП3-9а-16-220 кОм 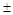20 % ОЖ0.467.012 ТУ.

4. Нарисуйте схему замещения резисторов. Перечислите паразитные параметры резистора. Как влияют паразитные параметры на граничную частоту резистора?

5. Перечислите основные электрические параметры резисторов постоянного и переменного сопротивления.

6. Объясните механизм появления электросопротивления тонких резис­тивных пленок. Какими факторами определяется значение ТКС тонкой пленки?

7. Почему электропроводность композиционного резистора зависит от приложенного напряжения?

8. Укажите области применения и приведите основные характеристики углеродистых тонкослойных резисторов.

9. Укажите области применения и приведите основные характеристики тонкослойных металлодиэлектрических и металлоокисных резисторов.

10. Укажите области применения и приведите основные характеристики пленочных и объемных композиционных резисторов.

11. Укажите области применения и приведите основные характеристики проволочных резисторов.

12. Объясните систему обозначений марок высокоомных сплавов для проволочных резисторов. Расшифруйте пример записи марки сплава в констру­кторских документах: МНМцАЖ3-12-0,3-0,3; МНМцА36-13-13; Х20Н80.

13. Укажите области применения и приведите основные характеристики резисторов переменного сопротивления.

14. Перечислите области применения варисторов.

15. Объясните принцип действия, укажите области применения и приведите основные характеристики терморезисторов.

16. Объясните принцип действия, укажите области применения и приведите основные характеристики фоторезисторов и резисторных оптронов.

17. Объясните принцип действия и дайте определение основных характеристик магниторезисторов

Примеры решения задач

Расчет характеристик резисторов

Пример 2.1. Рассчитать температуру перегрева D T резистора при следующих исходных данных:

1) номинальное сопротивление R _н = 220 Ом;

2) ток через резистор I = 0,1 А;

3) площадь охлаждения поверхности резистора S = 100 см².

Решение.

В процессе работы ре­зистор нагревается и температура его пе­регрева D T от­но­си­тель­но окружающей среды определяется соотношением

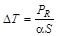, K, (2.1)

где D T = Т_R – Т ₀, Т_R – температура резистора, °С; Т ₀ » 20 °C – тем­пе­­ра­тура окружающей среды; P_R = I ² R – мощность элект­ри­чес­ко­го то­ка, рассеиваемая резистором, Вт; I – ток через резистор, А; R – элек­­три­ческое сопротивление резистора, Ом; S – пло­щадь по­верх­нос­ти ре­зис­тора, м²; a 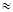10 Вт/К×м² – коэф­фи­ци­ент теплоотдачи с еди­ни­цы площади по­верх­ности резистора.

1. Рассчитываем мощность электрического тока, рассеиваемую в резисторе:

P_R = (0,1)²220=2,2 Вт.

2. Подставляя полученное значение в формулу (2.1), получим:

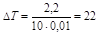K.

Ответ: D T = 22 К.

Пример 2.2. Рассчитать удельную мощность рассеяния P _уд резистора с параметрами, приведенными в примере 2.1.

Решение.

При рас­четах размеров ре­зи­с­тора поль­зу­ют­ся по­­нятием до­­­пус­ка­емой удель­­ной мощ­нос­ти рас­­се­я­ния ре­зис­тора P _уд, пред­став­ляющей отношение номинальной мощ­ности P _н, рас­се­и­ва­емой ре­зис­тором, к единице пло­ща­ди поверхности S ре­зис­то­ра:

P _уд = 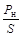, Вт/м². (2.2)

 

1. Полагая P _н= P_R и подставляя полученные значения в формулу (2.2), получаем:

P _уд = 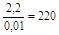Вт/м².

Ответ: P _уд = 220 Вт/м². Для резисторов общего при­­­ме­нения значение P _уд обы­ч­но при­­­­нимается равным 500¼1000 Вт/м².

Пример 2.3. Рассчитать коэффициент нагрузки резистора по мощности K_Р при следующих сходных данных:

1) номинальная мощность рассеяния P _н = 2 Вт;;

2) рабочая мощность рассеяния P _раб = 0,2 Вт.

Решение.

Отношение фактической (ра­бочей) мощ­ности рассеяния ре­­­зис­­тора при под­­ключении его в элек­три­чес­кую схему P _раб к но­­­ми­на­­льной мощ­ности рас­сеяния P _нна­зы­вается коэф­фи­ци­ен­том наг­­рузки рези­стора по мощ­ности, K_Р:

. (2.3)

Ответ. В данном случае . Для повышения надеж­нос­ти работы электрической схемы обыч­но пользуются этим значением K_Р, вы­­­­бирая стан­дартные ре­зис­торы с более вы­сокой но­ми­­наль­ной мо­щ­­­но­стью рас­се­я­ния P _н, име­ю­щие боль­­шие раз­меры, и, со­­от­вет­­­ственно, боль­шую по­верх­ность охла­жде­ния S.

Пример 2.4. Рассчитать требуемую номинальную мощность рассеяния резистора при следующих сходных данных:

1)номинальное сопротивление R _н = 5100 Ом;

3) коэффициент нагрузки резистора по мощности K_Р =0,2;

4) рабочее напряжение U _раб=36 В.

Решение.

Расчет номинальной мощности рассеяния резистора производится по формуле

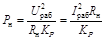, Вт, (2.4)

где I _раб – рабочий ток, протекающий через резистор, А.

1. Воспользовавшись первым выражением в формуле (2.4), получим

Вт.

Ответ. Расчетное значение P _н=1,27 Вт. Выбираем ближайшее стандартное значение P _н=2 Вт. Из формулы (2.4) следует, что максимальное значение рабочего напряжения на резисторе можно рассчитать по формуле

.

Пример 2.5. Рассчитать граничную частоту f _гр, резистора с номинальным сопротивлением R _н = 5100 Ом.

Решение.

Паразитные электрические параметры резисторов оказывают влияние на характеристики электрической схемы при относительно высоких частотах сигнала, превышающих 1¼3 МГц. Граничную частоту f _гр, выше которой начинает сказываться влияние паразитных параметров, можно оценить по фор­му­ле

, Гц. (2.5)

где R_R – соп­ро­­тивление РЭ, Ом; С_R 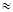10^–13...10^–12 Ф – электрическая ем­кость между выводами резистора.

1. Полагая С_R =1 пФ из формулы (2.5) получим

Гц.

Ответ. f _гр=31,2 МГц.

Пример 2.6. Рассчитать диаметр и длину обмоточного провода проволочного точного резистора. Исходные данные для расчета:

1)номинальное сопротивление R _н = 5100 Ом;

2) номинальная мощность рассеяния P _н = 2 Вт;

3) материал провода – константан (сплав МНМц40-1,5, r = 0,48×10^–6 Ом×м).

Решение.

1. Вычислим значение тока I _н через резистор по формуле

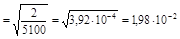A. (2.6)

2. Рассчитаем диаметр провода d _oрезистивного элемента (РЭ) без изоляции:

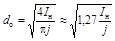,. (2.7)

где I _н– значение тока через резистор, А.

Плотность тока j выбирается в зависимости от допустимо­го нагрева резистора, диаметра провода и условий ох­лаж­­дения; для расчетов могут быть приняты следующие зна­чения плотности тока: для стабильных резисторов 1¼2 А/мм², для нагрузочных (гасящих) резисторов 5¼10 А/мм², для ре­зисторов из микропровода 200¼300 А/мм².

Для стабильного резистора выберем допустимую плотность тока j = 2 А/мм². Подставляя это значение в формулу (2.7), получим:

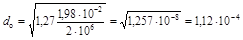м = 0,112 мм.

Из таблицы П.4 [9] выбираем стандартный диаметр провода d ₀=0,12 мм.

В качестве провода намотки из таблицы 2.2 выбираем эмалированный провод ПЭВКТ-1 со стандартным диаметром d _из= 0,145 мм.

3. По формуле

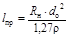, м, (2.8)

где r – удельное сопротивление провода, Ом×мм²/м, определим длину обмоточного провода l _пр:

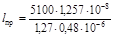= 105,2 м.

Ответ. d ₀=0,12 мм; d _из = 0,145 мм; l _пр =105,2 м.

Пример 2.7. Рассчитать размеры цилиндрического каркаса D _к и L _н, удельную мощность рассеяния P _уд проволочного резистора (рис.2.1). Исходные данные:

1) число витков рядовой обмотки N =1000;

2) коэффициент неплотности укладки провода a=1,2;

3) число слоев обмотки m =1;

4) длина обмоточного провода l _пр=105,2 м;

5) номинальная мощность рассеяния резистора P _н = 2 Вт;

6) диаметр намоточного провода в изоляции d _из= 0,145 мм.

 

Решение.

1. По формуле 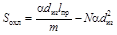(2.9)

рассчитываем величину площади поверхности охлаждения S _охл резистора с m -слойной рядовой намоткой:

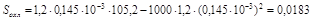м²

2. Рассчитываем длину намотки L _н по формуле:

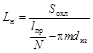. (2.10)

Число витков обмотки резистора N для различных номинальных сопротивлений резисторов находится в пределах 50…1000. Задавшись величиной N =1000, получаем длину намотки:

м.

Выберем значение длины щек каркаса d_к = 3 мм. Тогда общая длина каркаса L _к = 174 + 2×3 = 180 мм.

3. Рассчитаем диаметр каркаса D _к по формуле

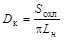
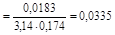м. (2.11)

Конструктивно выполнимое значение D _к = 6¼40 мм.

4. Из выражения (2.2) рассчитываем удельную мощность рассеяния P _удрезистора:

Вт/м².

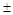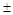Для точных резисторов с допусками 0,25; 0,5; 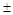1,0% значение удельной мощности рассеяния Р _уд = 50¼500 Вт/м²; для резисторов общего применения с допустимой температурой перегрева 50¼60 °С величина Р _уд = 1000......1500 Вт/м², для нагрузочных резисторов (нап­ример, в цепях питания аппаратуры) Р _уд = 3000¼5000 Вт/м².

Полученная величина P _уднаходится в пределах рекомендованных значений для точных и прецизионных резисторов.

Ответ. L _к=180 мм; D _к=33,5 мм; P _уд=109 вт/м².

Пример 2.8. Вывести выражение (2.7) для расчета диаметра обмоточного провода без изоляции d _o.

Решение.

Воспользуемся формулой для допустимой плотности тока j, протекающего через резистивный элемент:

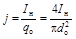, А/мм², (2.12)

где I _н– значение тока через резистор, А; q _o – сечение провода, мм².

Ответ. Из формулы (2.12) следует, что диаметр провода резистивного элемента без изоляции равен

.

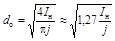Пример 2.9. Вывести выражения (2.9) и (2.10) для расчета площади поверхности охлаждения резистора S _охл и длины намотки L _н.

Решение.

Площадь поверхности охлаждения резистора S _охл оценивается по формуле

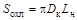. (2.13)

Число витков m -слойной рядовой намотки определяется из формулы

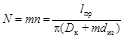, (2.14)

где m =1, 3, 5,…, l _пр – длина провода намотки.

Число витков n в одном слое рядовой намотки:

, (2.15)

где a = 1,1¼1,3 – коэффициент неплотности укладки про­вода, d _из – диаметр провода в изоляции.

Подставляя в формулу (2.13) выражения для диаметра каркаса D _к из (2.14) и длины намотки L _н из (2.15) рассчитываем величину площади поверхности охлаждения S _охл резистора с m -слойной рядовой намоткой:

.

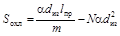Подставляя в формулу (2.13) выражение для диаметра каркаса D _к из (2.14), рассчитываем длину намотки L _н (при заданном числе витков обмотки N):

.

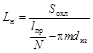Ответ. . .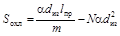

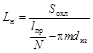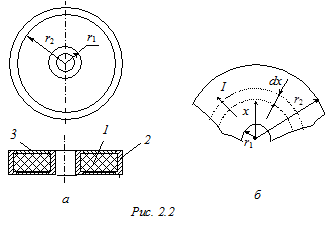Пример 2.10. Определить сопротивление R _э шайбового высокочастотного резистора (рис.2.2, а), изготовленного из пленки пиролитического углерода с сопротивлением квадрата R _□ =300 Ом. На рис.2.2, а. обозначено: 1 – керамический диск с отверстием; 2 – металлизированные контактные площадки, выполняющие функции выводов резистора; 3 – резистивный элемент (пленка пироуглерода).

Решение.

Ток I через такой резистор проходит радиально по резистивной пленке (рис.2.2, б). Выделим в пределах резистивного элемента узкий кольцеобразный участок шириной dx, имеющий координату x, отсчитываемую от центра. Сопротивление этого участка dR_x = ρ dx /(2π x δ), где ρ/δ= R _□ – сопротивление квадрата резистивной пленки, δ – толщина резистивной пленки.

Сопротивление резистивного элемента, расположенного с одной стороны диэлектрического диска с отверстием (шайбы),

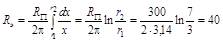Ом.

Ответ. R _э=40 Ом.