Тема 6. Системы линейных алгебраических уравнений
Основные понятия СЛАУ
Системой состоящей из m линейных уравнений с n неизвестными называется система вида
 (1)
(1)
где  ,
, 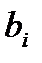 - числа,
- числа,  - неизвестные, n – число неизвестных, m – число уравнений.
- неизвестные, n – число неизвестных, m – число уравнений.
Решением линейной системы (1) называется упорядоченная совокупность чисел  которые при подстановке вместо неизвестных обращают каждое уравнение системы в верное равенство.
которые при подстановке вместо неизвестных обращают каждое уравнение системы в верное равенство.
Линейная система называется неоднородной, если среди свободных членов имеются отличные от нуля. Если все свободные члены равны нулю, то линейная система называется однородной. Однородная система имеет вид
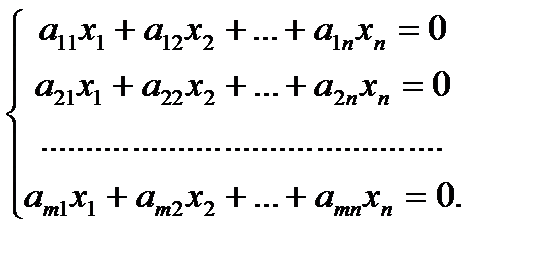 (2)
(2)
Система, имеющая хотя бы одно решение, называется совместной, а система не имеющая решений, - несовместной. Отметим, что однородная система всегда совместна, так как она имеет нулевое решение.
Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если имеет более одного решения.
Две системы называются эквивалентными или равносильными, если любое решение одной из них является так же решением другой и обратно, т.е. если имеют одно и то же множество решений. Любые две несовместные системы считаются эквивалентными.
Элементарными преобразованиями системы называются следующие преобразования:
1) умножение уравнения системы на число, отличное от нуля;
2) прибавление к одному уравнению системы другого ее уравнения, умноженного на любое число;
3) перестановка местами двух уравнений системы.
Определителем системы называется определитель матрицы А из коэффициентов уравнений этой системы

Матрица  полученная из основной присоединением столбца из свободных членов называется расширенной матрицей системы.
полученная из основной присоединением столбца из свободных членов называется расширенной матрицей системы.
Решение СЛАУ по формулам Крамера
Пусть дана система n линейных уравнений с n неизвестными.
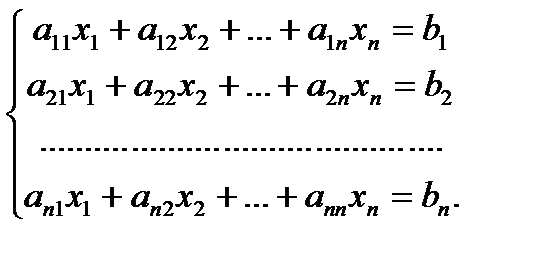
Обозначим через D определитель системы, а через Dk определитель, полученный заменой в определителе D столбца из коэффициентов при неизвестной хk столбцом свободных членов системы, т.е.


где k – одно из чисел 1, 2, …, n.
Теорема.
1) Если 
 система (2.3) имеет единственное решение, определяемое по формулам:
система (2.3) имеет единственное решение, определяемое по формулам:  .
.
2) Если  =
=  =0, система имеет бесконечно много решений.
=0, система имеет бесконечно много решений.
3) Если  =0, а хотя бы один из
=0, а хотя бы один из 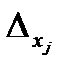
 система не имеет решений.
система не имеет решений.
Пример. Решить систему линейных уравнений по формулам Крамера:
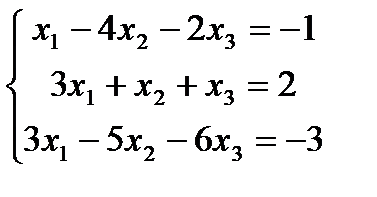
Решение:
Найдем определитель матрицы коэффициентов системы

Так как Δ # 0, то заданная система уравнений имеет единственное решение. Для этого вычислим определители Δj, получающиеся из определителя Δ путем замены в нем столбца, состоящего из коэффициентов при хj, столбцом свободных членов.




Отсюда

Ответ:
Примеры:
1. Рассмотрим систему  , решенную в предыдущем разделе методом Гаусса, и применим к ней правило Крамера. Найдем все нужные определители:
, решенную в предыдущем разделе методом Гаусса, и применим к ней правило Крамера. Найдем все нужные определители:
 следовательно, система имеет единственное решение.
следовательно, система имеет единственное решение.

Отсюда 
2.  . Здесь
. Здесь  поскольку имеет два одинаковых столбца.
поскольку имеет два одинаковых столбца.
Следовательно, система не имеет единственного решения. Найдем  и
и 
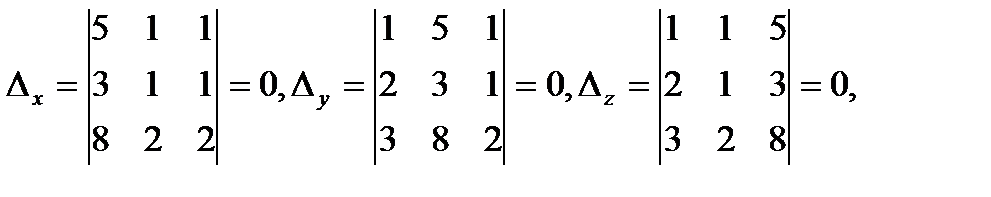 поэтому система имеет бесконечно много решений.
поэтому система имеет бесконечно много решений.
3.  . Для этой системы
. Для этой системы  но
но 
следовательно, решений нет.