1.1. Основы метода конечных элементов
Метод конечных элементов (МКЭ) в настоящее время является стандартом при решении задач механики твердого тела посредством численных алгоритмов. Популярный в свое время метод конечных разностей, а также претендовавший на универсальность метод граничных элементов (граничных интегральных уравнений) сейчас занимают достаточно узкие ниши, ограниченные исследовательскими или специальными задачами. МКЭ занял лидирующее положение благодаря возможности моделировать широкий круг объектов и явлений. Абсолютное большинство конструктивных элементов, узлов и конструкций, изготовленных из самых разнообразных материалов, имеющих различную природу, могут быть рассчитаны посредством МКЭ. При этом, разумеется, нужно учитывать неизбежные при любой численной аппроксимации условности и погрешности. Поэтому вопрос соответствия между расчетной моделью и реальностью является, пожалуй, основным при использовании программ анализа. Несмотря на то, что такие программы имеют более или менее подробную документацию, они все равно остаются в определенной степени черными ящиками. Это означает определенную непредсказуемость результатов, а также некоторый произвол в их интерпретации. Следовательно, качество заключений, принимаемых на основе результатов, всецело зависит от квалификации, а также, применительно к расчету на прочность, принципиального знакомства с основами МКЭ.
Метод конечных элементов является численным методом решения дифференциальных уравнений, встречающихся в физике и технике. Возникновение этого метода связано с решением задач космических исследований (1950 г.). Впервые он был опубликован в работе Тернера, Клужа, Мартина и Топпа. Эта работа способствовала появлению других работ; был опубликован ряд статей с применениями метода конечных элементов к задачам строительной механики и механики сплошных сред. Важный вклад в теоретическую разработку метода сделал в 1963 г. Мелош, который показал, что метод конечных элементов можно рассматривать как один из вариантов хорошо известного метода Рэлея-Ритца. В строительной механике метод конечных элементов минимизацией потенциальной энергии позволяет свести задачу к системе линейных уравнений равновесия.
Связь метода конечных элементов с процедурой минимизации привела к широкому использованию его при решении задач в других областях техники. Метод применялся к задачам, описываемым уравнениями Лапласа или Пуассона. Решение этих уравнений также связано с минимизацией некоторого
функционала. В первых публикациях с помощью метода конечных элементов решались задачи распространения тепла. Затем метод был применен к задачам гидромеханики, в частности к задаче течения жидкости в пористой среде.
Область применения метода конечных элементов существенно расширилась, когда было показано, что уравнения, определяющие элементы в задачах строительной механики, распространения тепла, гидромеханики, могут быть легко получены с помощью таких вариантов метода взвешенных невязок, как метод Галёрюша или способ наименьших квадратов.
Метод конечных элементов из численной процедуры решения задач строительной механики превратился в общий метод численного решения дифференциального уравнения или системы дифференциальных уравнений. Этот прогресс был достигнут за пятнадцатилетий период, за счет совершенствования быстродействующих цифровых вычислительных машин, необходимых для более точного расчета конструкций летательных аппаратов, а также благодаря помощи Национального комитета по исследованию космического пространства. Вычислительная машина позволила ускорить проведение многих сложных численных расчетов. Изучение космического пространства потребовало выделения средств на проведение фундаментальных исследований и стимулировало совершенствование универсальных вычислительных программ. Метод конечных элементов применяется при проектировании самолетов, ракет, различных пространственных оболочек и т. п.
1.2. Основная концепция метода конечных элементов
Основная идея метода конечных элементов состоит в том, что любую непрерывную величину, такую, как температура, давление и перемещение, можно аппроксимировать дискретной моделью, которая строится на множестве кусочно-непрерывных функций, определенных на конечном числе подобластей. Кусочно-непрерывные функции определяются с помощью значений непрерывной величины в конечном числе точек рассматриваемой области.
В общем случае непрерывная величина заранее неизвестна и нужно определить значения этой величины в некоторых внутренних точках области. Дискретную модель, однако, очень легко построить, если сначала предположить, что числовые значения этой величины в каждой внутренней точке области известны. После этого можно перейти к общему случаю. Итак, при построении дискретной модели непрерывной величины поступают следующим образом:
1. В рассматриваемой области фиксируется конечное число точек. Эти точки называются узловыми точками или просто узлами.
2. Значение непрерывной величины в каждой узловой точке считается переменной, которая должна быть определена.
3. Область определения непрерывной величины разбивается наконечное число подобластей, называемых элементами. Эти элементы имеют общие узловые точки и в совокупности аппроксимируют форму области.
4. Непрерывная величина аппроксимируется на каждом элементе полиномом, который определяется с помощью узловых значений этой величины. Для каждого элемента определяется свой полином, но полиномы подбираются таким образом, чтобы сохранялась непрерывность величины вдоль границ элемента. Основная концепция метода конечных элементов может быть наглядно проиллюстрирована на одномерном примере заданного распределения температуры в стержне, показанном на рис. 1.1.
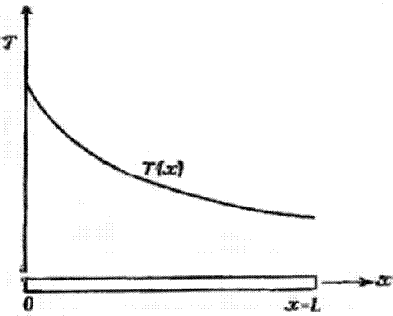
Рисунок 1.1. Распределение температуры в одномерном стержне
5. Рассматривается непрерывная величина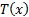 
, область определения – отрезок 
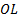вдоль оси х. Фиксированы и пронумерованы пять точек на оси (рис. 1.2, а). Это узловые точки; совсем не обязательно располагать их на равном расстоянии друг от друга. Очевидно, можно ввести в рассмотрение и более пяти точек, но этих пяти вполне достаточно, чтобы проиллюстрировать основную идею метода. Значения Т(х) в данном случае известны в каждой узловой точке. Эти фиксированные значения представлены графически на фиг. 1.2б и обозначены в соответствии с номерами узловых точек через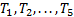 
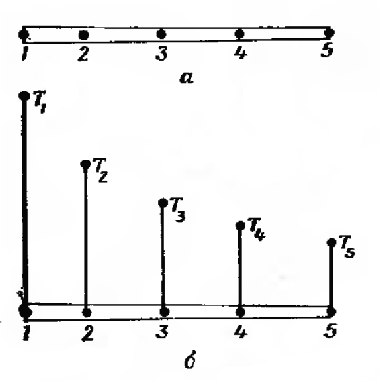
Рисунок 1.2. Узловые точки и предполагаемые значения Т(х).
Разбиение области на элементы может быть проведено двумя различными способами. Можно, например, ограничить каждый элемент двумя соседними узловыми точками, образовав четыре элемента (рис. 1.3, а), или разбить область на два элемента, каждый из которых содержит три узла (рис.1.3б). Соответствующий элементу полином определяется по значениям Т(х) в узловых точках элемента. В случае разбиения области на четыре элемента, когда на каждый элемент приходится по два узла, функция элемента будет линейна по х (две точки однозначно определяют прямую линию).
б)
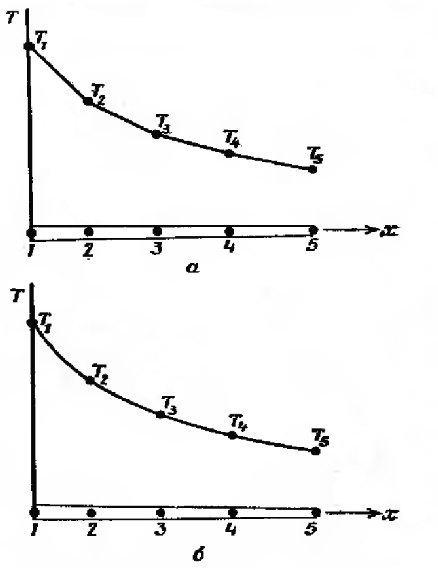
Рис. 1.3 Деление области на элементы
Рис. 1.4. Дискретные модели для одномерного температурного поля
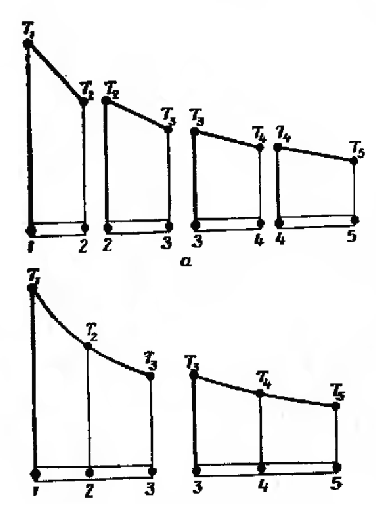
Окончательная аппроксимация Т(х) будет состоять, из четырех кусочно-линейных функций, каждая из которых определена на отдельном элементе (фиг.1.4а).
Другой способ разбиения области на два элемента с тремя узловыми точкам и приводит к представлению функции элемента в виде полинома второй степени. В этом случае окончательной аппроксимацией Т(х) будет совокупность двух кусочно-непрерывных квадратичных функций. Отметим, что это приближение будет именно кусочно-непрерывным, так как углы наклона графиков обеих этих функций могут иметь разные значения в третьем узле.
В общем случае распределение температуры неизвестно и мы хотим определить значения этой величины в некоторых точках. Методика построения дискретной модели остается точно такой же, как описано выше, но с добавлением одного дополнительного шага. Снова определяются множество узлов и значения температуры в этих узлах которые теперь являются переменными,так как они заранее неизвестны. Область разбивается на элементы, на каждом из которых определяется соответствующая функция элемента.
Узловые значения Т(х) должны быть теперь «отрегулированы» таким образом, чтобы обеспечивалось «наилучшее» приближение к истинному распределению температуры. Это «регулирование» осуществляется путем минимизации некоторой величины, связанной с физической сущностью задачи. Если рассматривается задача распространения тепла, то минимизируется функционал, связанный с соответствующим дифференциальным уравнением. Процесс минимизации сводится к решению систем линейных алгебраических уравнений относительно узловых значенийT(x)
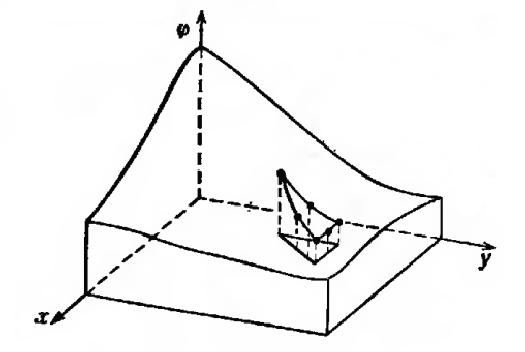
Рис. 1.5. Моделирование двумерной скалярной функции с помощью треугольных и четырехугольных элементов
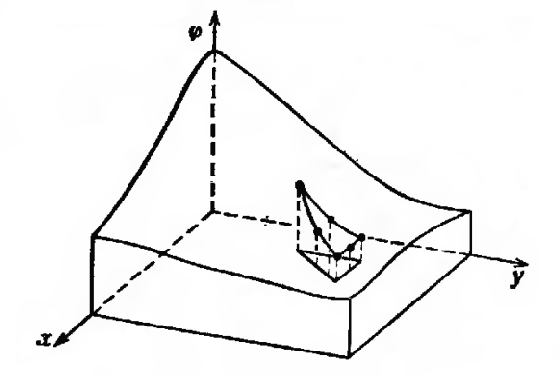
Рис. 1.6. Моделирование двумерной скалярной функции с помощью квадратичного треугольного элемента
1.3. Конечные элементы в SolidWorks
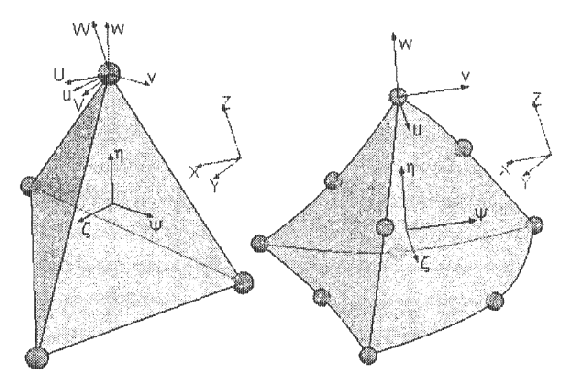
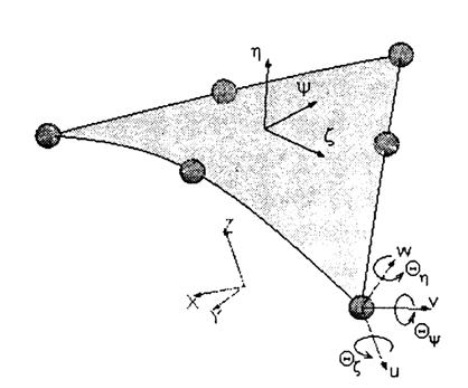
Рис. 1.7. Объемные конечные элементы
Рис. 1.8. Параболический конечный элемент
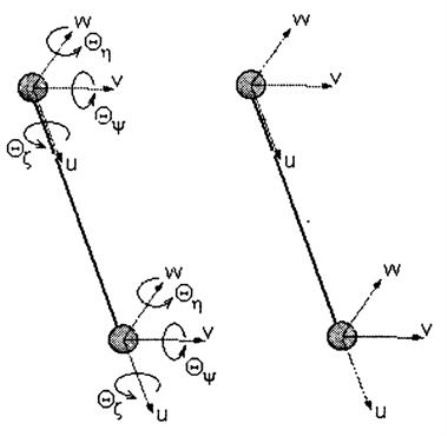
Рис. 1.9. Конечный элемент балки и стержня