Пример выполнения задачи №1

Задание № 2.

Тема: «Определение реакций связей плоских систем сил»

Выполнил студент группы 222-ЧС ____________________________

 

ЗАДАНИЕ ДИСТАНЦИОННОГО ОБУЧЕНИЯ

По исходным данным согласно варианту (номер по списку в журнале) и пользуясь примером (см. ниже) решить задачи №1 и №2.

Задание выполнять непосредственно в данном документе (в примерах решения задач) заменяя исходные данные своими и изменяя рассчитанные по формулам величины – также своими, полученными после соответствующих вычислений.

Возможно выполнение задания в рабочей тетради.

 

Занятие №3 (практическое) «Определение реакций связей плоских систем сил»

Задача №1 (плоская система сходящихся сил)

 

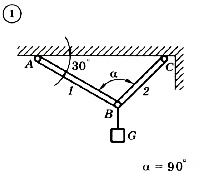
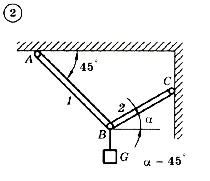
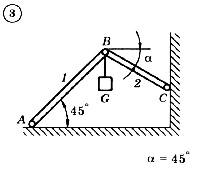
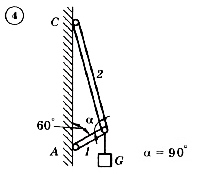
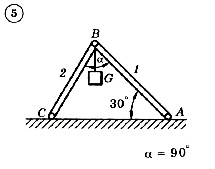
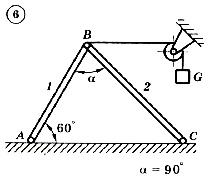
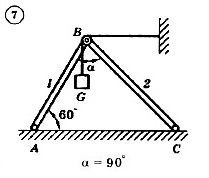
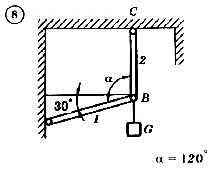
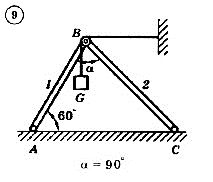
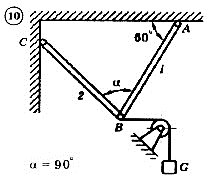
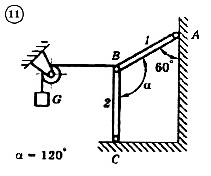
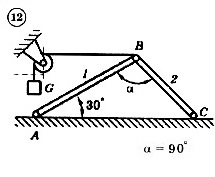
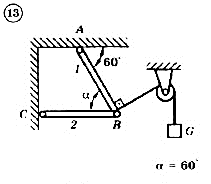
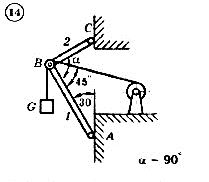
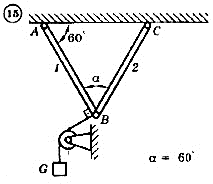
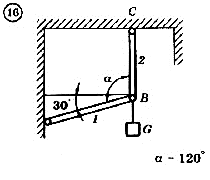
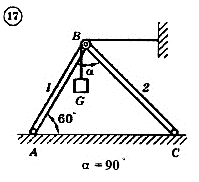
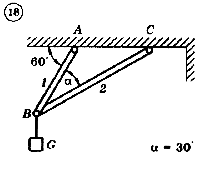
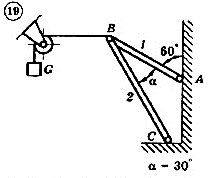
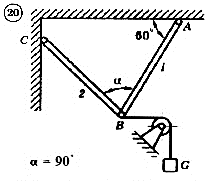
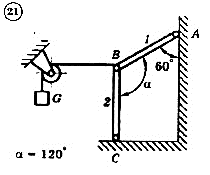
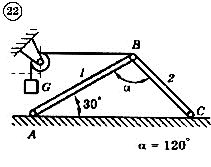
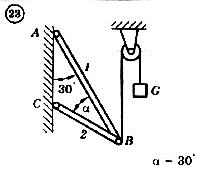
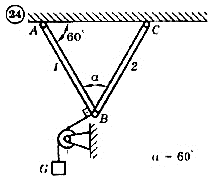
Для механической системы согласно варианту определить усилия в стержнях 1 и 2. Номер схемы и вариант соответствует порядковому номеру по списку в журнале.

Стержни, блоки и канаты невесомы. Вес груза G = mg, где g – ускорение свободного падения (g » 10 м/с²), m – масса груза в кг, равная числу номера варианта (схемы) умноженному на 100. Например, для варианта (схемы) №1 m = 100 кг для варианта (схемы) №2 – m = 200 кг и т.д.

 

Пример выполнения задачи №1

 

Груз весом G = 2 кН (рис. 1) удерживается краном, состоящим из двух невесомых стержней в шарнирах АВ и АС, прикрепленных к вертикальной стене и составляю­щих с ней углы α ₁ = 60° и α ₂ = 40°. В точке А подвешен блок, через который перекинут грузовой трос, идущий к блоку в точке D и составляющий со стеной угол α ₃ = 60°.

Весом троса и блока, а также размерами блока можно пренебречь. Определить усилия в стержнях.

Решение. Рассмотрим находящийся в равновесии груз (рис. 2).

На него действуют две силы: сила тяжести G и сила натяжения троса N ₁. Поскольку система сил уравнове­шена, можно сделать очевидный вывод: сила натяжения троса направлена внутрь троса и по модулю равна весу груза N ₁ = G.

Если для любого блока (рис. 3) пренебречь трением на его оси, то силы натяжения ветвей его троса одинаковы N ₁ = N ₂ (что легко видеть из уравнения моментов относи­тельно центра блока).

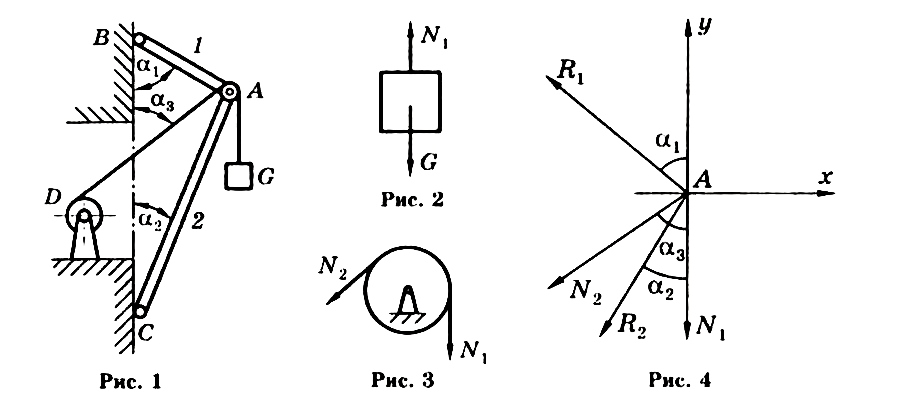
Теперь в качестве объекта равновесия можно рассмот­реть мысленно вырезанный узел в точке А (или, что то же самое, блок с прилежащей к нему частью троса). На этот узел будут действовать силы натяжения ветвей троса N ₁ и N ₂и реакции R ₁, и R ₂ стержней АВ и АС (рис. 4).

Реакции опорных стержней направлены, как извест­но, вдоль этих стержней. Направим их внутрь стержней, считая изначально стержни растянутыми.

Составим теперь уравнения равновесия как уравнения проекций сил на оси х и у (для системы сходящихся сил), учитывая, что силы R ₁, R ₂ и N ₂составляют углы α ₁, α ₂ и α ₃ с осью у.

 

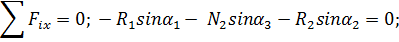
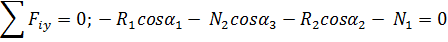
Отсюда, учитывая, что N ₁ = N ₂ = 2 кН, получаем

 

 

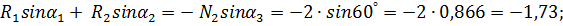
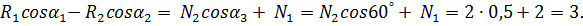
Решая эту систему уравнений, находим

 

 

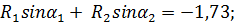
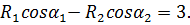
Подставляем в уравнения значения углов и их синусов и косинусов (пользуясь таблицей синусов и косинусов):

 

 

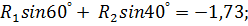
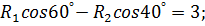
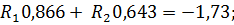
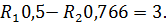
Из первого и второго уравнения выражаем R ₁ через R ₂:

 

 

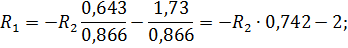
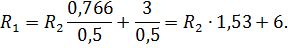
Так как левые части уравнений равны, то и правые части так же равны:

 

 

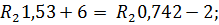
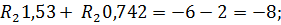
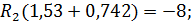
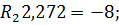
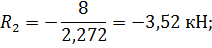
Знак «минус» у величины реакции R ₂ означает, что она имеет направление, противоположное принятому, то есть стержень АС не растянут, а сжат.

Подставив значение R ₂ в одно из уравнений, находим R ₁

 

 

 

 

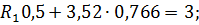
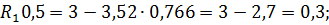
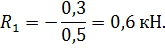
Ответ: R ₁ = 0,6 кН; R ₂ = 3,52 кН.

 

Выполним проверку, построив силовой многоугольник. Для этого определим масштаб: 1 кН = 2 см.

Тогда векторы G = N ₁ = N ₂ = 2 × 2 = = 4 см;

R ₁ = 0,611 × 2 ≈ 1,22 см;

R ₂ = 3,52 × 2 ≈ 7 см.

И построим многоугольник, выдерживая углы между векторами сил, согласно заданию (рис. 5).

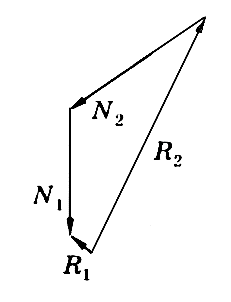
Рис. 5.

Литература:

1. Вереина Л.И. Техническая механика: Учеб. для нач. проф. образования: Учеб. пособие для сред. проф. образования. - М.: ПрофОбр-Издат,2002.-176 с.

Стр. 14.

2. Диевскнй В. А., Малышева И. А. Теоретическая механика. Сборник заданий: Учеб­ное пособие. 2-е изд., испр. — СПб.: Издательство «Лань», 2009. — 192 с.: ил. — (Учебники для вузов. Специальная литература).

Стр. 10.

 

 

Задача №2 (плоская система произвольно расположенных сил)

 

Для стальной двухопорной балки по схеме согласно варианту определить реакции опор. Номер схемы и вариант соответствует порядковому номеру по списку в журнале.

Исходные данные для решения задачи взять из таблицы 1 согласно варианту.

 

 

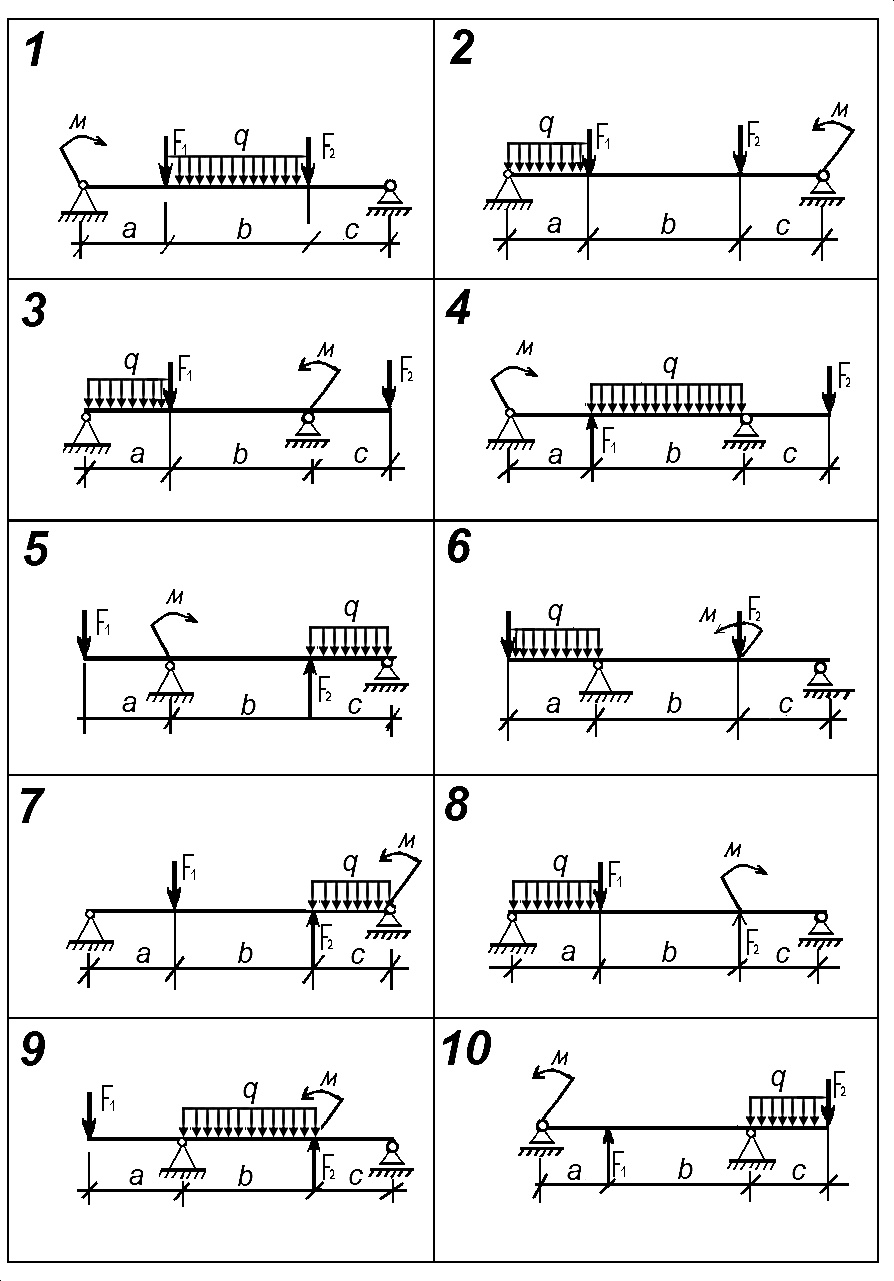
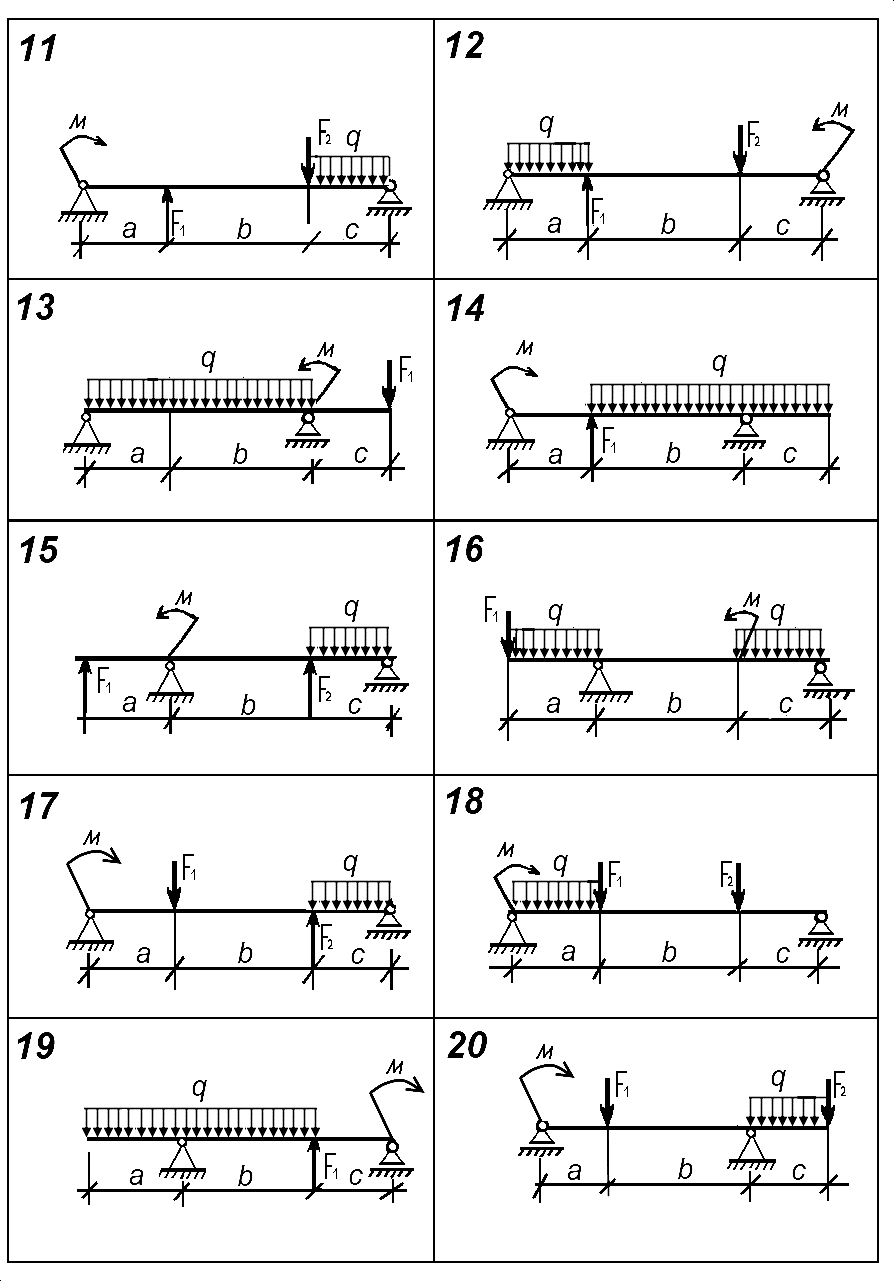
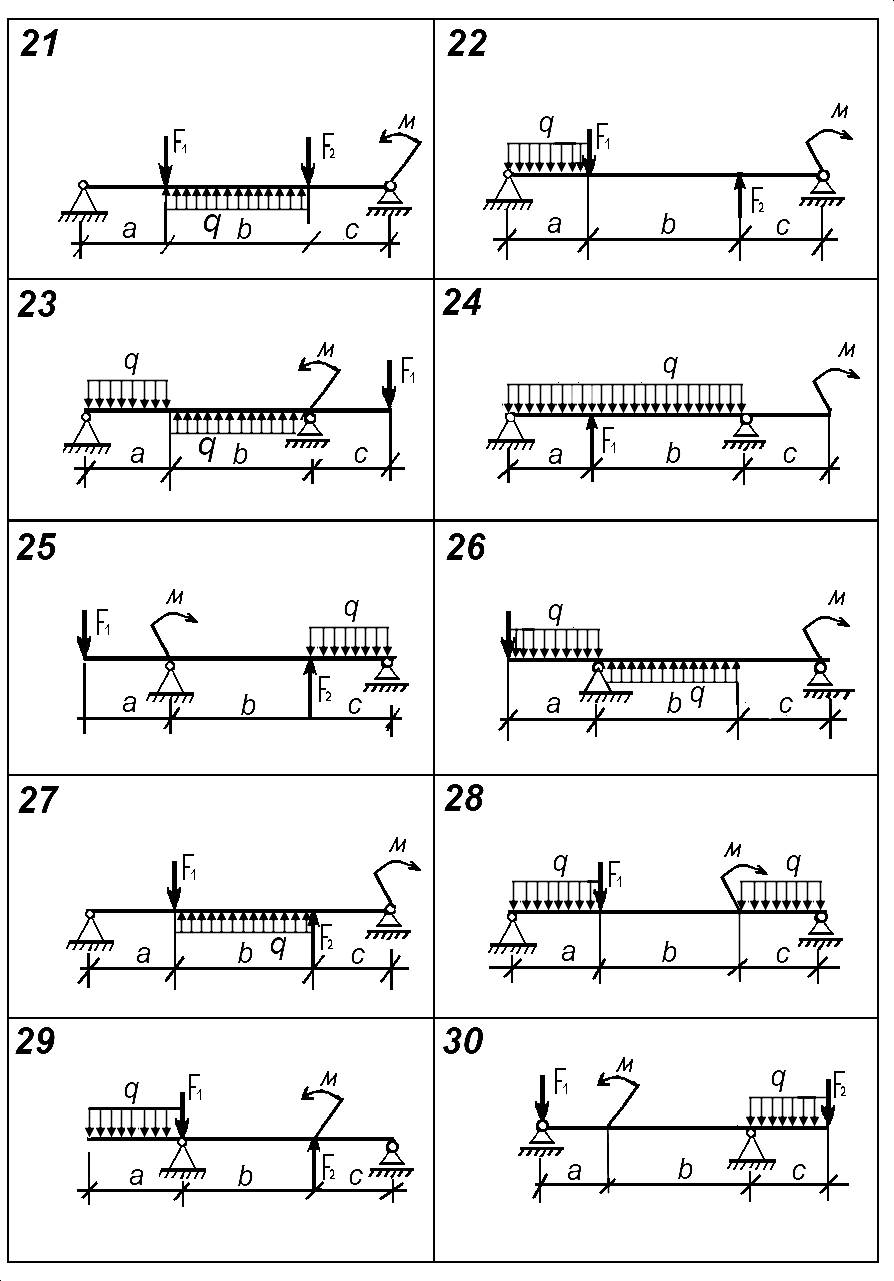
Таблица 1

Исходные данные

 

№ варианта и схемы	F 1, кН	F 2, кН	q, кН/м	m, кН·м	а, м	b, м	c, м
1, 11, 21
2, 12, 22					1.5
3, 13, 23
4, 14, 24					2.5
5, 15, 25
№ варианта и схемы	F 1, кН	F 2, кН	q, кН/м	m, кН·м	а, м	b, м	c, м
6, 16, 26
7, 17, 27					2.5
8, 18, 28
9, 19, 29					1.5
10, 20, 30