С любой точкой А плоскости XOY мы можем связать радиус-вектор  и установить взаимно однозначное соответствие множества комплексных чисел z = a + b
и установить взаимно однозначное соответствие множества комплексных чисел z = a + b  с множеством радиус-векторов с координатами (a, b) (рисунок 3).
с множеством радиус-векторов с координатами (a, b) (рисунок 3).
y
b A(a,b)
r

O a x
Рисунок 3 – Связь прямоугольной и полярной систем координат
Тогда
a = r cos  , b = r sin
, b = r sin  ,
,
z = a + bi = r (cos  + i sin
+ i sin  ),
),
есть так называемая тригонометрическая форма комплексного числа.
Определение.  = r
= r  расстояние от О до А называется модулем комплексного числа.
расстояние от О до А называется модулем комплексного числа.
Определение. Аргументом arg z комплексного числа z называется угол  между положительным направлением оси ОХ и радиусом-вектором ОА.
между положительным направлением оси ОХ и радиусом-вектором ОА.
 .
.
Чтобы определить  однозначно, нужно знать положение точки A на плоскости.
однозначно, нужно знать положение точки A на плоскости.
Если точка A находится в 1 или 4 четверти, то  .
.
Если точка A находится во 2 или 3 четверти, то  .
.
Умножение и деление комплексных чисел, записанных в тригонометрической форме
Умножение и деление комплексных чисел удобнее выполнить, если эти числа записаны в тригонометрической форме.
Пусть
 ,
,
тогда
 ,
,
а
 .
.
Формула Муавра
При любом натуральном n 
 =
=  =
=  ,
,
или
 =
= 
– это так называемая формула Муавра позволяющая находить целую степень комплексного числа.
Извлечение корней n-ой степени из комплексного числа
Пусть комплексное число z задано в тригонометрической форме
z = r (cos  + i sin
+ i sin  )
)  0 + 0 i.
0 + 0 i.
Тогда
 .
.
k =  .
.
Пример 1 Записать в тригонометрической форме комплексные числа:
 .
.
Модуль этого комплексного числа  числу z соответствует точка (1;1)
числу z соответствует точка (1;1)  I четверти (рисунок 4). Поэтому
I четверти (рисунок 4). Поэтому
 .
.
Запишем

y
1 (1+i)

0 1 x
Рисунок 4 – Число 1+i в комплексной плоскости
Окончательно запишем 
Пример 2 Найти произведение и частное комплексных чисел z 1 и z 2
 .
.
Решение:
 ,
,
 .
.
Пример 3 Вычислить  .
.
Решение:

Пример 4 Найти все значения корня 4-й степени из z = 
Здесь r = 1,  Тогда
Тогда  .
.
Тогда при k = 0, 
k = 1, 
k = 2, 
k = 3, 
Задачи для решения
1 Записать данные комплексные числа в тригонометрической форме, определив их модули и аргументы:
a) z = 2 + 2  i, б) z =
i, б) z =  + i,
+ i,
в) z =1- i, г) z = -4,
д) z = 3 i, е) z = -2 i.
ж) z = -10; з) z = 6-6i;
и) z = -1  i; к) z =1
i; к) z =1  i.
i.
2 Найти произведение и частное комплексных чисел  и
и  в тригонометрической форме:
в тригонометрической форме:
а) 
б) 
3 Вычислить:
а)  +
+  б)
б) 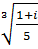 ;
;
в)  г)
г) 
д)  ж)
ж)  ;
;
з)  и)
и) 
к)  ; л)
; л)  ;
;
м)  н)
н) 
о) 
4 Найти значения  при n = 2, 3, 4, 6.
при n = 2, 3, 4, 6.
Двучленные уравнения
Определение. Уравнения вида  называются двучленными, где
называются двучленными, где 
Решение этого уравнения находится в виде:
 .
.
Решение двучленных уравнений сводится к извлечению корней n-ой степени из комплексных чисел.
Пример Решить уравнение  = 0.
= 0.
Решение
Перепишем уравнение в виде  будем рассматривать
будем рассматривать  32 как комплексное число и представим его в тригонометрической форме:
32 как комплексное число и представим его в тригонометрической форме:
 .
.
Теперь по правилу извлечения корня из комплексного числа найдем

где k следует придать значения 0, 1, 2, 3, 4. Получим пять корней нашего уравнения:



Уравнение имеет один действительный корень и четыре комплексных.
Задачи для решения
1 Решить уравнения:
а)  б)
б) 
в)  г)
г) 
д)  е) 8
е) 8 
ж) 16  з)
з) 
и) -  ; к) 3
; к) 3 
Геометрическое решение уравнений
Найти геометрическое решение неравенства  .
.
Решение:  ,
,  ,
,  ,
,  . Найдем модуль комплексного числа
. Найдем модуль комплексного числа  .
.
 .
.
Получим  (1), возведем в квадрат правую и левую части (1), получим
(1), возведем в квадрат правую и левую части (1), получим  .
.
 – геометрически это круг с центром в точке A (-1; 1) и радиусом 3 (рисунок 5).
– геометрически это круг с центром в точке A (-1; 1) и радиусом 3 (рисунок 5).
y
-1 0 x
Рисунок 5 – Решение неравенства
Задачи для решения
1 Найти решение систем:









