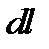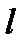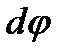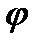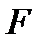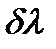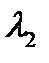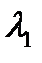Лабораторная работа №5
Цель работы: Исследование дифракции Фраунгофера на щели и дифракционной решетке. Определение параметров дифракционной решетки: угловой и линейной дисперсии, разрешающей способности. Измерение ширины дифракционных максимумов и определение длины волны падающего излучения.
Приборы и принадлежности: Оптическая скамья, источник монохроматического излучения, линза, экран, щель переменной ширины, дифракционная решетка.
Введение
Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле – любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Благодаря дифракции волны могут попадать в область геометрической тени, огибать препятствия, проникать через небольшие отверстия в экранах и т.д.
Явление дифракции обусловлено волновой природой света. При решении задач, связанных с дифракцией (т.е. при решении задач о распространении света за непрозрачными экранами и отверстиями в них) широко применяется принцип Гюйгенса-Френеля, позволяющий получить удовлетворительное решение этих задач наиболее элементарным способом.
Принцип Гюйгенса-Френеля сводится к следующим утверждениям: каждая точка волнового фронта световой волны является источником вторичных волн; вторичные волны когерентны и интерферируют между собой; интенсивность световой волны в некоторой точке пространства является результатом интерференции вторичных волн, дошедших до данной точки.
Принцип Гюйгенса-Френеля является основным постулатом волновой оптики. Справедливость этого постулата подтверждается совпадением результатов наблюдения и выводов, полученных на его основе.
Рассмотрим два вида дифракции:
1. Точечный источник света и точка наблюдения находятся на конечном расстоянии от препятствия. Этот случай дифракции соответствует сферическому фронту волны, падающей на препятствие, и называется дифракцией Френеля.
2. Точечный источник света находится настолько далеко от препятствия, что лучи, падающие на препятствие, можно считать параллельными. Этот тип дифракции (в параллельных лучах) называется дифракцией Фраунгофера.
Краткая теория
ДИФРАКЦИЯ ОТ ОДНОЙ ЩЕЛИ
Пусть параллельный пучок монохроматического света падает нормально на непрозрачный экран  , в котором имеется узкая щель
, в котором имеется узкая щель 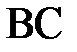 шириной
шириной  , рис.1. Согласно принципу Гюйгенса-Френеля все точки щели будут источниками вторичных волн, колебания в которых происходят в одной фазе, т.к. плоскость фронта совпадает с плоскостью щели.
, рис.1. Согласно принципу Гюйгенса-Френеля все точки щели будут источниками вторичных волн, колебания в которых происходят в одной фазе, т.к. плоскость фронта совпадает с плоскостью щели.
Рассмотрим волны, распространяющиеся от точек плоскости щели 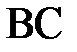 в направлении, составляющем с первоначальным угол
в направлении, составляющем с первоначальным угол  . Если на пути лучей поставить линзу
. Если на пути лучей поставить линзу 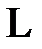 с фокусным расстоянием
с фокусным расстоянием  , оптическая ось которой перпендикулярна плоскости экрана
, оптическая ось которой перпендикулярна плоскости экрана 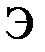 , то все лучи, идущие под углом
, то все лучи, идущие под углом  , соберутся в фокальной плоскости, в точке
, соберутся в фокальной плоскости, в точке 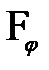 .
.
Линза обладает замечательным свойством – она не создает дополнительной разности фаз между лучами, собираемыми в одной точке изображения. Вследствие этого оптические пути лучей, соответствующих фронту 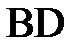 и пришедших в точку
и пришедших в точку 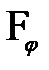 будут одинаковы или таутохронны.
будут одинаковы или таутохронны.
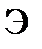
|
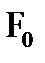
|

|
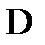
|
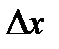
|
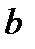
|
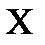
|

|
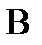
|
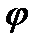
|
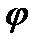
|
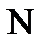
|
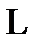
|
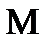
|
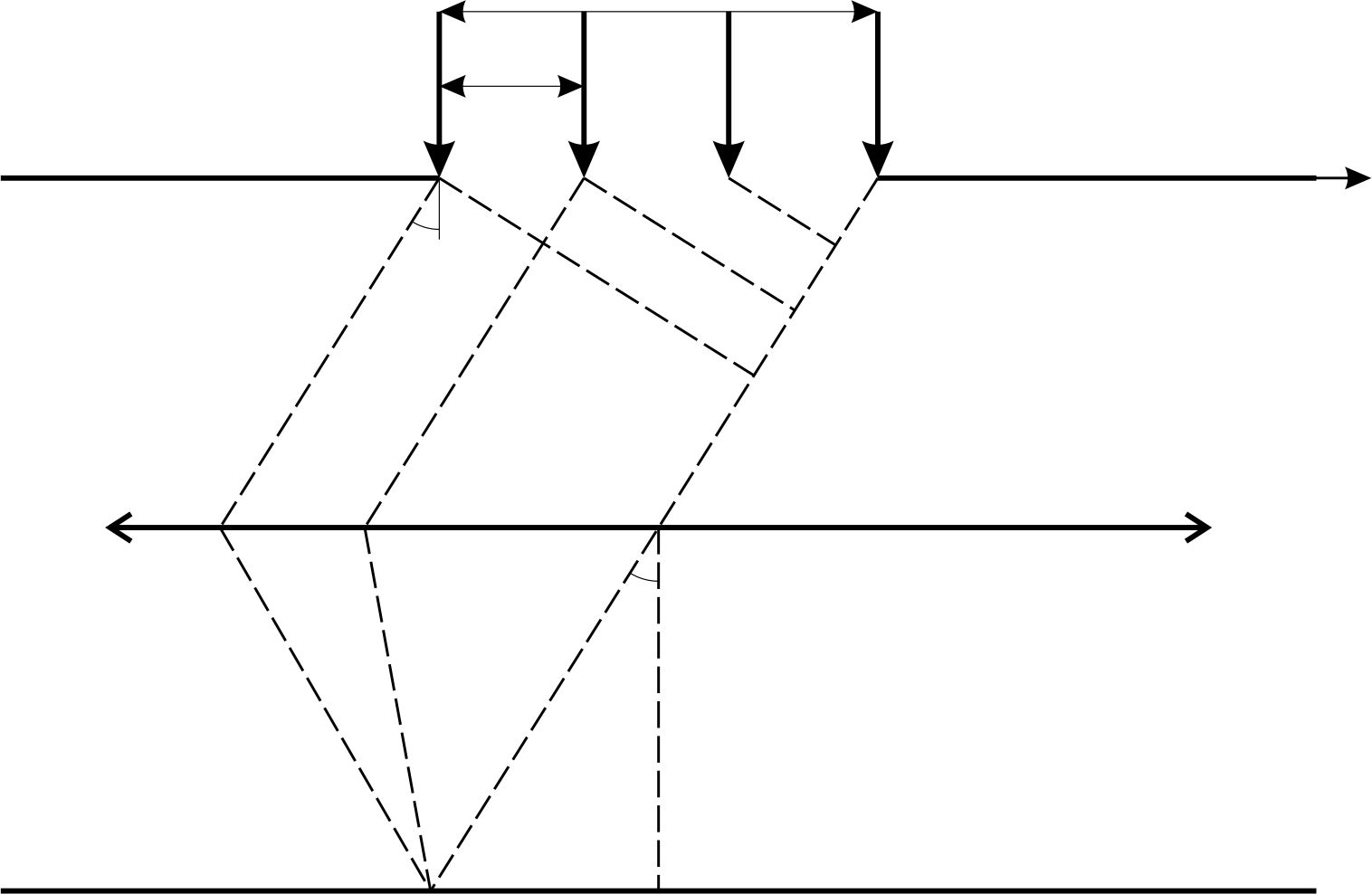
Рис. 1.
Для расчета интерференционной картины в точке 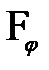 применим метод зон Френеля. Для этого мысленно разделим
применим метод зон Френеля. Для этого мысленно разделим 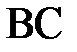 на ряд зон шириной
на ряд зон шириной 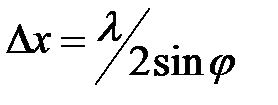 . Тогда, как видно из рис.1, лучи идущие от соответственных точек соседних зон (например, от их краев), придут в точку
. Тогда, как видно из рис.1, лучи идущие от соответственных точек соседних зон (например, от их краев), придут в точку 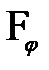 с разностью хода
с разностью хода
 (1)
(1)
т.е. в противофазе. Это значит, что волны, пришедшие в точку 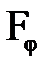 от соседних зон, гасят друг друга.
от соседних зон, гасят друг друга.
Число зон Френеля 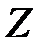 , укладывающихся на ширине щели
, укладывающихся на ширине щели 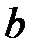 в зависимости от угла дифракции
в зависимости от угла дифракции  , будет различным:
, будет различным:
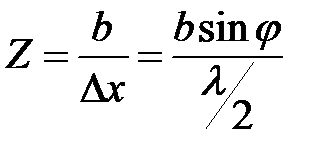 (2)
(2)
Разность хода лучей, идущих под углом  от краев щели, определяется выражением:
от краев щели, определяется выражением:
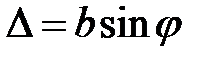 (3)
(3)
Для углов 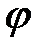 , под которыми видно целое число зон, возможны случаи:
, под которыми видно целое число зон, возможны случаи:
1. 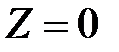 , что соответствует
, что соответствует 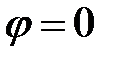 . Колебания от всех участков щели придут в точку
. Колебания от всех участков щели придут в точку 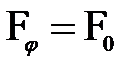 в одинаковой фазе
в одинаковой фазе 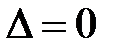 , образуя центральный максимум (максимум нулевого порядка).
, образуя центральный максимум (максимум нулевого порядка).
2. Число зон Френеля четное.
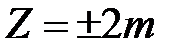 ,
, 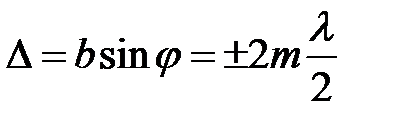 , (
, (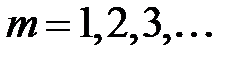 ) (4)
) (4)
В точках фокальной плоскости, для которых выполняется условие (4), будут наблюдаться темные полосы (дифракционные минимумы).
3. Число зон Френеля нечетное (кроме 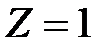 ).
).
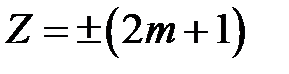 ,
, 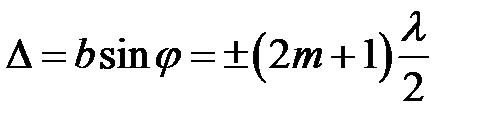 , (
, (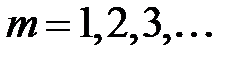 ) (5)
) (5)
В точках фокальной плоскости, удовлетворяющих условию (5), будут наблюдаться дифракционные максимумы.
Знак 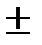 указывает на то, что max и min будут располагаться по обе стороны от центрального максимума под углами
указывает на то, что max и min будут располагаться по обе стороны от центрального максимума под углами 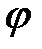 и
и  . Углы, под которыми видна только одна зона (
. Углы, под которыми видна только одна зона (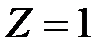 ) находятся из условия:
) находятся из условия:
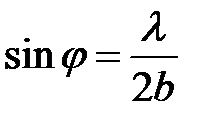 . (6)
. (6)
Для углов, под которыми на ширине щели будет укладываться не целое число зон Френеля, будет наблюдаться промежуточная освещенность между max и min.
РАСПРЕДЕЛЕНИЕ ИНТЕНСИВНОСТИ В ДИФРАКЦИОННОЙ КАРТИНЕ
Интенсивность побочных max (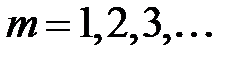 ) будет меньше интенсивности центрального max. Это видно из того, что с увеличением
) будет меньше интенсивности центрального max. Это видно из того, что с увеличением 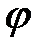 ширина зоны Френеля
ширина зоны Френеля 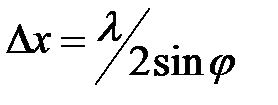 уменьшается, следовательно, с увеличением угла
уменьшается, следовательно, с увеличением угла  уменьшается и поток энергии в данном направлении.
уменьшается и поток энергии в данном направлении.
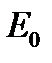
|
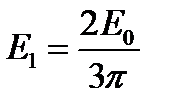
|
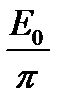
|
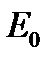
|
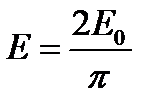
|
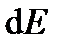
|
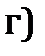
|
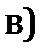
|
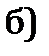
|
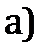
|
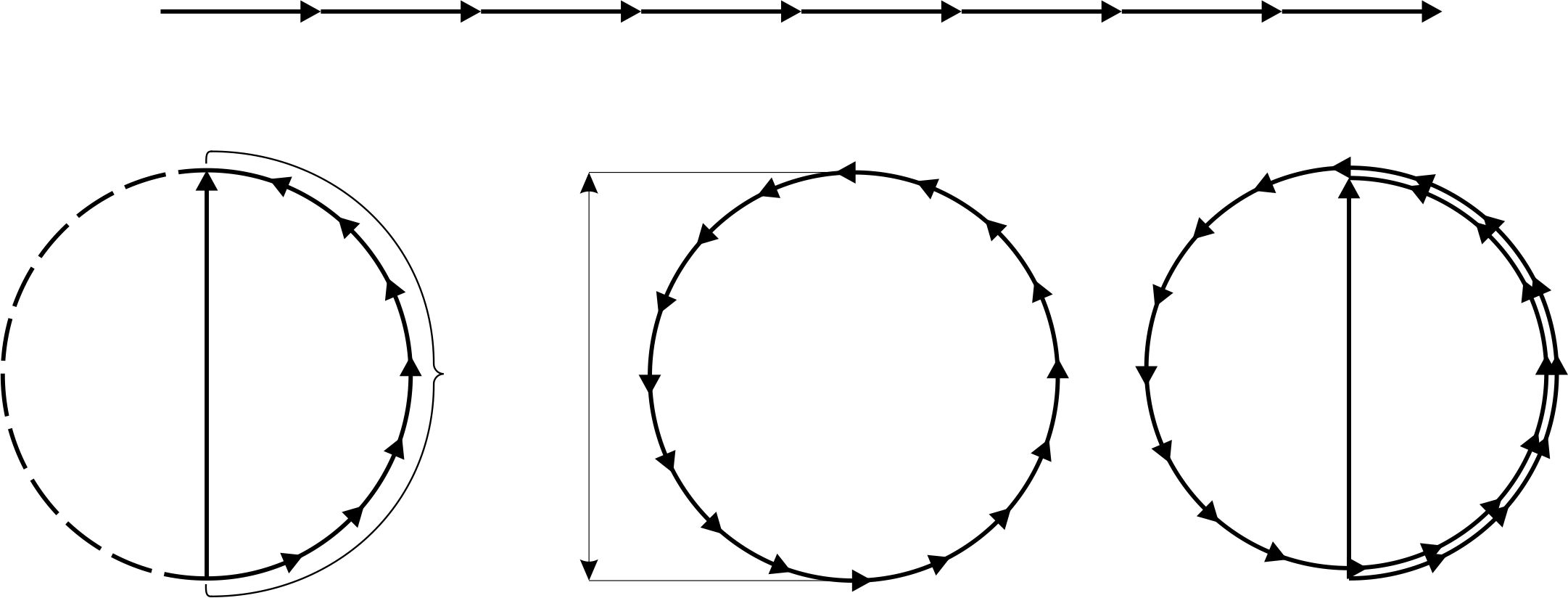
Рис. 2.
Задача об интенсивностях в максимумах при дифракции Фраунгофера от одной щели может быть решена методом графического сложения амплитуд. Разобьем открытую часть волновой поверхности падающей волны на одинаковые по величине очень узкие зоны 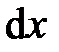 .
.
Амплитуды колебаний 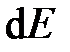 от каждой зоны
от каждой зоны 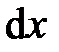 одинаковы и колебание данной зоны отстает по фазе от колебания предыдущей зоны на одну и ту же величину
одинаковы и колебание данной зоны отстает по фазе от колебания предыдущей зоны на одну и ту же величину 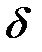 , зависящую от угла
, зависящую от угла 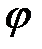 . При
. При 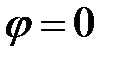 разность фаз соседних зон равна 0 и векторная диаграмма имеет вид, показанный на рис. 2а. Амплитуда результирующего колебания
разность фаз соседних зон равна 0 и векторная диаграмма имеет вид, показанный на рис. 2а. Амплитуда результирующего колебания  равна алгебраической сумме амплитуд складываемых колебаний. Если разность фаз колебаний, соответствующих краям щели равна
равна алгебраической сумме амплитуд складываемых колебаний. Если разность фаз колебаний, соответствующих краям щели равна 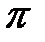 (что соответствует
(что соответствует 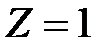 ), векторы
), векторы 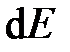 располагаются вдоль полуокружности (рис. 2б) длиной
располагаются вдоль полуокружности (рис. 2б) длиной 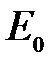 . Следовательно, для результирующей амплитуды
. Следовательно, для результирующей амплитуды  получаются значения
получаются значения  , откуда
, откуда
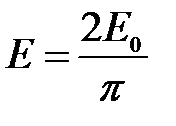 . (7)
. (7)
В случае, когда 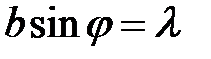 (
(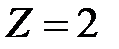 ), колебания от краев щели отличаются по фазе на
), колебания от краев щели отличаются по фазе на 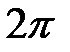 . Соответствующая диаграмма изображена на рис. 2в. Векторы
. Соответствующая диаграмма изображена на рис. 2в. Векторы 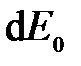 располагаются вдоль окружности длинной
располагаются вдоль окружности длинной 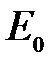 . Результирующая амплитуда равна нулю, т.е. имеет место первый минимум. Первый побочный max (
. Результирующая амплитуда равна нулю, т.е. имеет место первый минимум. Первый побочный max (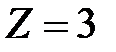 ) наблюдается при условии
) наблюдается при условии 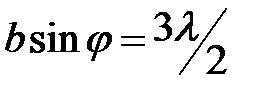 . В этом случае колебания от краев щели по фазе на
. В этом случае колебания от краев щели по фазе на 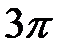 . Строя последовательно векторы
. Строя последовательно векторы 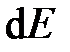 , мы обойдем полтора раза окружность диаметром
, мы обойдем полтора раза окружность диаметром 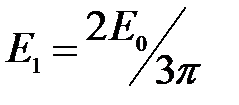 (рис. 2г). Таким образом, амплитуда
(рис. 2г). Таким образом, амплитуда  первого максимума составит
первого максимума составит 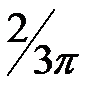 от амплитуды
от амплитуды  нулевого максимума. Учитывая, что интенсивности света пропорциональны квадратам амплитуд электрического поля волны, получим:
нулевого максимума. Учитывая, что интенсивности света пропорциональны квадратам амплитуд электрического поля волны, получим:
 (8)
(8)
То есть интенсивность побочных максимумов по сравнению с интенсивностью нулевого максимума убывает очень быстро.
Таким образом, центральный максимум значительно превосходит по интенсивности остальные максимумы; в нем сосредоточена основная доля светового потока, прошедшего сквозь щель.
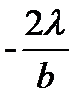
|
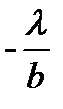
|

|

|

|
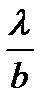
|
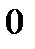
|
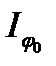
|
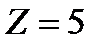
|
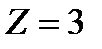
|

|
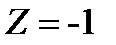
|
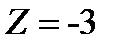
|

|
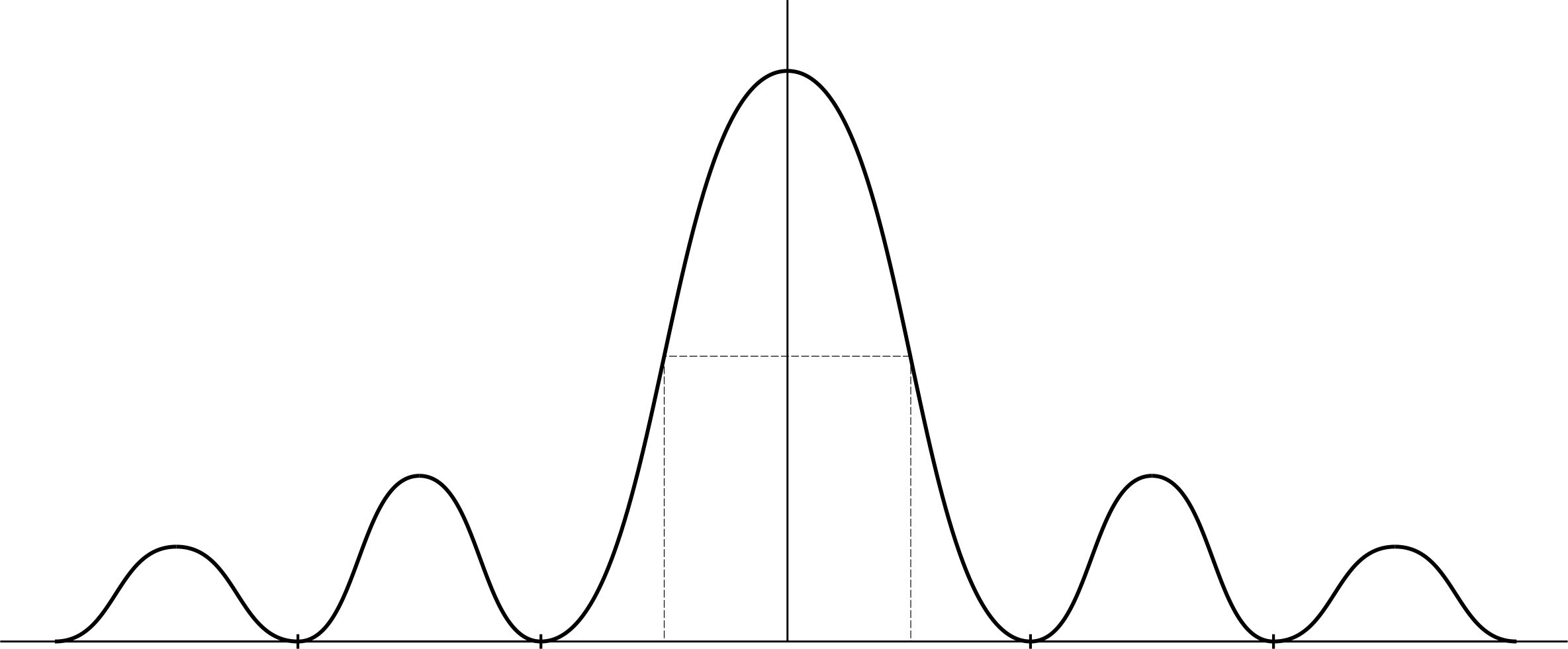
Рис. 3.
График интенсивности дифракционной картины от одной щели (без соблюдения масштаба по вертикали) изображен на рис. 3.
ШИРИНА ЦЕНТРАЛЬНОГО МАКСИМУМА ПРИ ДИФРАКЦИИ НА ОДНОЙ ЩЕЛИ
Определим ширину центрального максимума. Значение угла 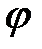 , соответствующие краям центрального максимума, удовлетворяют условию первого min:
, соответствующие краям центрального максимума, удовлетворяют условию первого min:
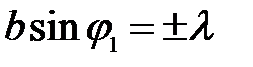 (9)
(9)
Следовательно, угловые размеры его равны:
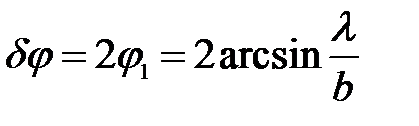 (10)
(10)
Линейные размеры центрального максимума в фокальной плоскости линзы 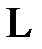 определяется из условия:
определяется из условия:
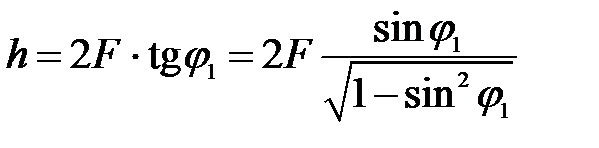 (11)
(11)
Подставляя значение 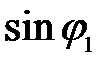 из условия первого min (9), получим:
из условия первого min (9), получим:
 (при
(при  ) (12)
) (12)
Как видно из форумы (12), с уменьшением ширины щели ширина центрального максимума увеличивается и при 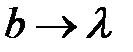 ,
, 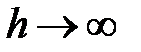 , т.е. центральный максимум захватывает весь экран, а освещенность экрана спадает от центра к краям, приближаясь к нулю.
, т.е. центральный максимум захватывает весь экран, а освещенность экрана спадает от центра к краям, приближаясь к нулю.
При увеличении ширины щели положение первых минимумов приближается к центру картины. Центральный максимум становится резче и резче. При этом увеличивается его интенсивность. При широкой щели ( ) в центре получится ее резкое изображение.
) в центре получится ее резкое изображение.
Общее число  максимумов для данной щели по одну сторону от нулевого максимума определяется из условия:
максимумов для данной щели по одну сторону от нулевого максимума определяется из условия:
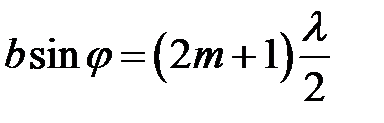 (при
(при 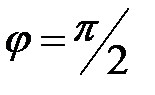 ) (13)
) (13)
ДИФРАКЦИОННАЯ РЕШЕТКА. ДИФРАКЦИЯ ОТ МНОГИХ ЩЕЛЕЙ
Дифракционной решеткой называется совокупность большого числа параллельных щелей, отстоящих друг от друга на одинаковых расстояниях (рис. 4)

|
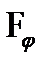
|

|

|
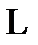
|

|

|

|
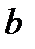
|
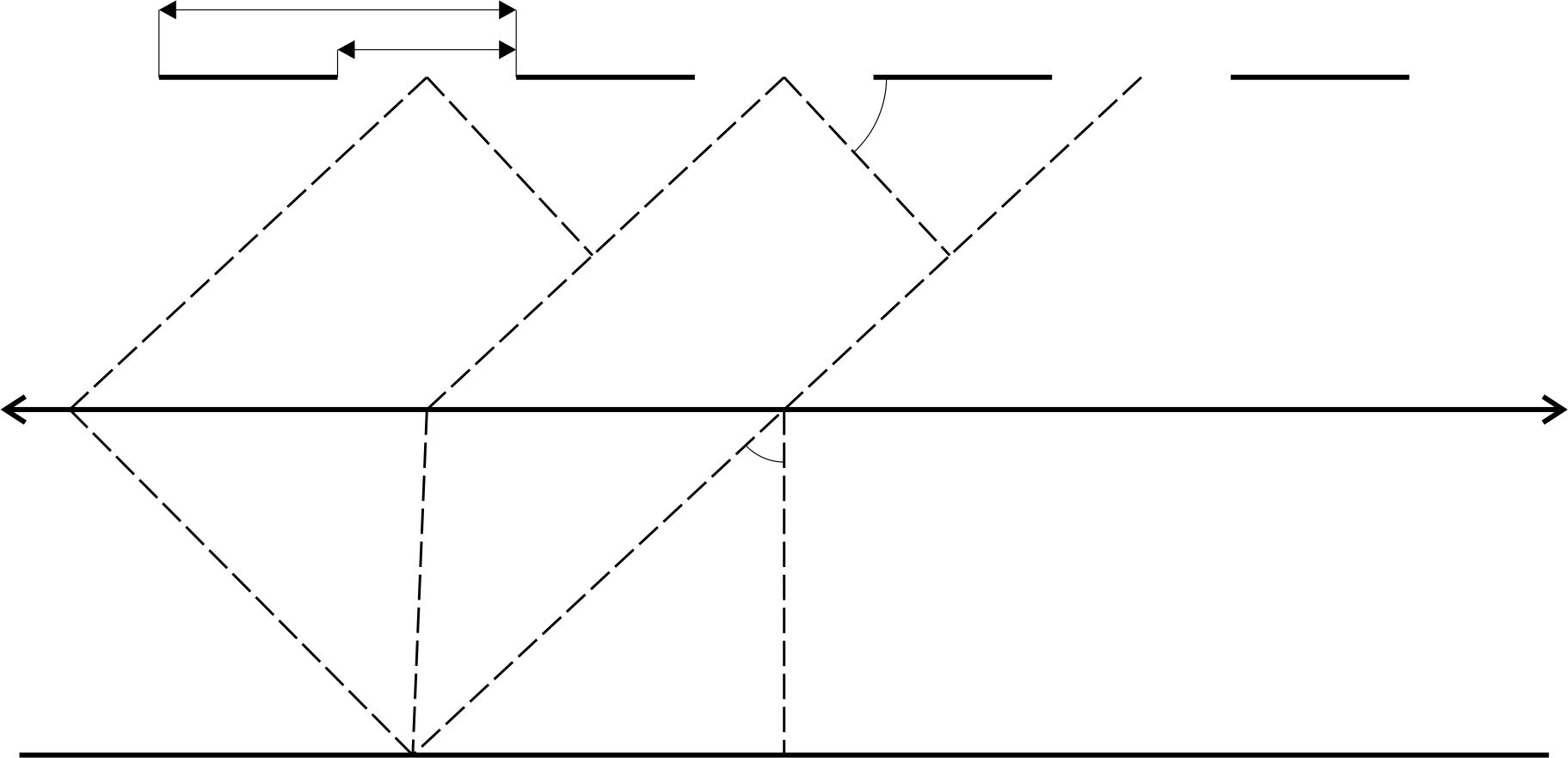
Рис. 4.
Суммарная ширина темного и светлого промежутка называется постоянной или периодом решетки (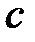 ).
).
Выясним характер дифракционной картины, получающейся на экране при падении на решетку перпендикулярно к ней плоской световой волны. Каждая из щелей даст на экране картину описываемую графиком, изображенном на рис. 3. Параллельные лучи от всех щелей придут в одно и то же место экрана (независимо от положения решетки центральный максимум лежит против центра линзы).
Если бы волны, приходящие в т. 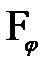 от разных щелей, были некогерентны, результирующая картина от
от разных щелей, были некогерентны, результирующая картина от 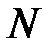 щелей отличалась бы от картины, создаваемой одной щелью, лишь тем, что интенсивности всех максимумов возросли бы в
щелей отличалась бы от картины, создаваемой одной щелью, лишь тем, что интенсивности всех максимумов возросли бы в 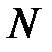 раз. Однако, волны, идущие от различных щелей, являются когерентными, поэтому для нахождения результирующей интенсивности нужно найти фазовые соотношения между световыми пучками, идущими от разных щелей.
раз. Однако, волны, идущие от различных щелей, являются когерентными, поэтому для нахождения результирующей интенсивности нужно найти фазовые соотношения между световыми пучками, идущими от разных щелей.
Для учета результата интерференции лучей, идущих от разных щелей, также как и в случае с одной щелью, разобьем открываемую щелями часть волновой поверхности на узкие зоны. Амплитудное значение напряженности электрического поля, создаваемого в т. 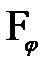 экрана
экрана 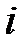 -ой зоной, обозначим
-ой зоной, обозначим 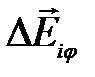 . Тогда вектор амплитуды результирующей волны, можно представить следующим образом:
. Тогда вектор амплитуды результирующей волны, можно представить следующим образом:
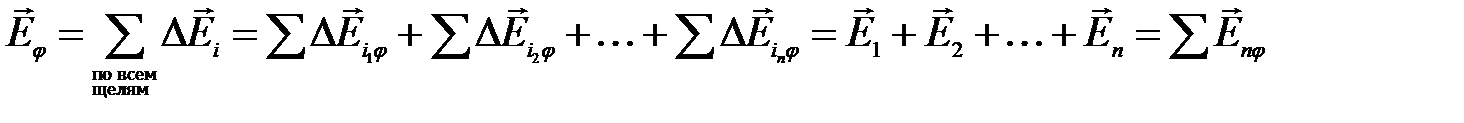 (14)
(14)
где 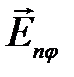 – вектор напряженности электрического поля, создаваемого в т.
– вектор напряженности электрического поля, создаваемого в т. 
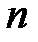 -ой щелью. Модули этих векторов одинаковы и зависят от угла
-ой щелью. Модули этих векторов одинаковы и зависят от угла 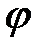 . Каждый следующий вектор
. Каждый следующий вектор 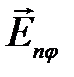 повернут относительно предыдущего
повернут относительно предыдущего  на один и тот же угол, равный разности фаз волн, возбуждаемых соседними щелями.
на один и тот же угол, равный разности фаз волн, возбуждаемых соседними щелями.
Для направлений, удовлетворяющих условию:
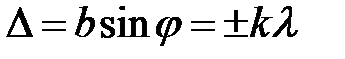 , (
, (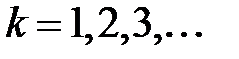 ) (15)
) (15)
Все  равны нулю. Амплитуда результирующей волны также будет равна нулю. Таким образом, условие минимума для одной щели является условием минимума и для решетки.
равны нулю. Амплитуда результирующей волны также будет равна нулю. Таким образом, условие минимума для одной щели является условием минимума и для решетки.
Если разность хода соответственных лучей от двух соседних щелей  удовлетворяющих условию
удовлетворяющих условию
 , (
, (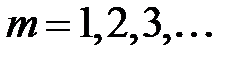 ) (16)
) (16)
что соответствует разности фаз 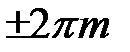 :
:
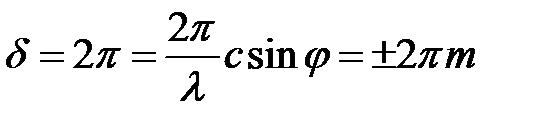 , (17)
, (17)
то волны, идущие от соседних щелей, взаимно усиливают друг друга, вследствие чего амплитуда колебаний в точке экрана 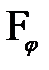 будет равна:
будет равна:
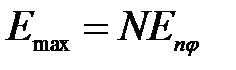 (18)
(18)
Формула (16) определяет положение максимумов интенсивности, называемых главными. Число m определяет порядок главного максимума. Поскольку интенсивность пропорциональна квадрату амплитуды волны, на основании формулы (18) будем иметь:
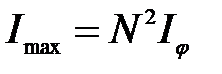 (19)
(19)
где 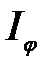 – интенсивность в максимуме, создаваемая лучами, идущими под углом
– интенсивность в максимуме, создаваемая лучами, идущими под углом 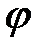 от одной щели.
от одной щели.
Кроме максимумов, определяемых условием (16), в промежутках между соседними главными максимумами имеется (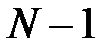 ) вторичных минимумов, между которыми располагаются вторичные максимумы. Эти минимумы возникают в тех направлениях, для которых волны, идущие от соседних щелей, гасят друг друга. Можно показать, что направление вторичных минимумов определяется условием:
) вторичных минимумов, между которыми располагаются вторичные максимумы. Эти минимумы возникают в тех направлениях, для которых волны, идущие от соседних щелей, гасят друг друга. Можно показать, что направление вторичных минимумов определяется условием:
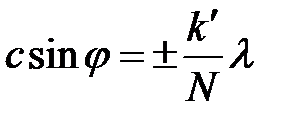 , (
, (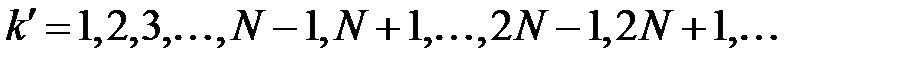 ) (20)
) (20)
(здесь 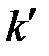 ' принимает любые целочисленные значения, кроме
' принимает любые целочисленные значения, кроме 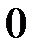 ,
, 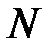 ,
, 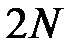 ,
,  т.е. кроме тех, при которых условие вторичных минимумов (20) переходит в условие максимума (16)).
т.е. кроме тех, при которых условие вторичных минимумов (20) переходит в условие максимума (16)).
Таким образом, дифракционная картина, получающаяся от решетки (без соблюдения масштаба по вертикали), имеет вид:

|
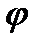
|
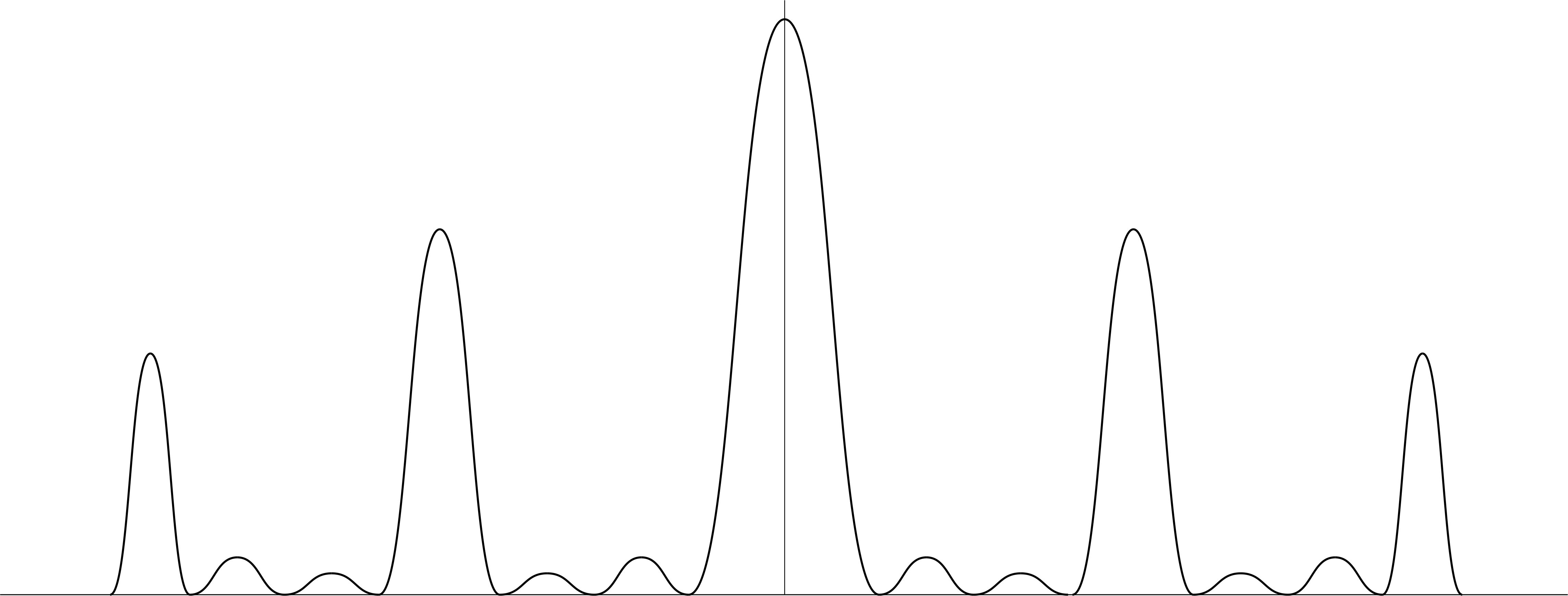
Рис. 5.
Из формулы (15) и (16) следует, что главный максимум 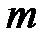 -го порядка придется на
-го порядка придется на 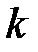 -ый минимум, если будет выполнено равенство:
-ый минимум, если будет выполнено равенство:
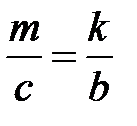 или
или  (21)
(21)
Это возможно, если 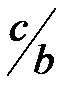 равно отношению целых чисел
равно отношению целых чисел 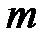 и
и 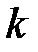 . Тогда главный максимум
. Тогда главный максимум 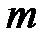 -го порядка наложится на
-го порядка наложится на 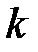 -ый минимум от одной щели, максимум
-ый минимум от одной щели, максимум 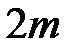 -го порядка на
-го порядка на 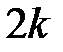 -ый минимум и т.д. в результате чего главные максимумы порядков
-ый минимум и т.д. в результате чего главные максимумы порядков  ,
, 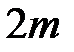 ,
, 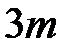 и т.д. будут отсутствовать. Обычно отношение
и т.д. будут отсутствовать. Обычно отношение 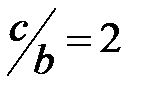 . В этом случае будут отсутствовать все четные главные максимумы.
. В этом случае будут отсутствовать все четные главные максимумы.
Наивысший порядок главных максимумов может быть определен из соотношения 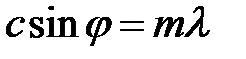 при
при 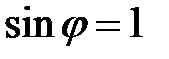 . Таким образом,
. Таким образом, 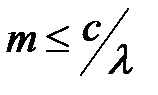 .
.
ШИРИНА ЦЕНТРАЛЬНОГО МАКСИМУМА ПРИ ДИФРАКЦИИ НА РЕШЕТКЕ
Найдем угловую ширину 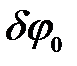 и линейные размеры
и линейные размеры 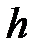 центрального max при дифракции от многих щелей. Положение примыкающих к нему дополнительных минимумов определяется условием:
центрального max при дифракции от многих щелей. Положение примыкающих к нему дополнительных минимумов определяется условием:
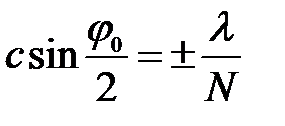 (22)
(22)
Угловые размеры центрального максимума:
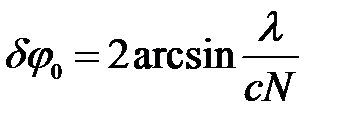 (23)
(23)
Линейные размеры центрального максимума в фокальной плоскости линзы будут равны:  , т.к.
, т.к. 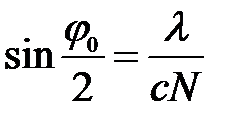 , то
, то
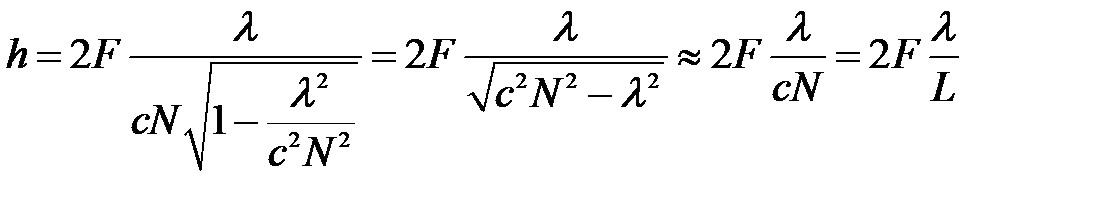 , (23)
, (23)
где 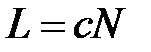 – длина дифракционной решетки. Следовательно, угловая ширина главных max уменьшается с увеличением длины решетки.
– длина дифракционной решетки. Следовательно, угловая ширина главных max уменьшается с увеличением длины решетки.
Положение главных максимумов зависит от длины волны  . При освещении решетки белым светом все максимумы, кроме центрального, разложатся в спектр, фиолетовый конец которого обращен к центру дифракционной картины, красный – наружу.
. При освещении решетки белым светом все максимумы, кроме центрального, разложатся в спектр, фиолетовый конец которого обращен к центру дифракционной картины, красный – наружу.
Расстояние 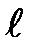 между серединой центрального максимума и
между серединой центрального максимума и 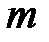 -тым максимумом, наблюдаемом под углом
-тым максимумом, наблюдаемом под углом 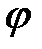 , определится выражением:
, определится выражением:
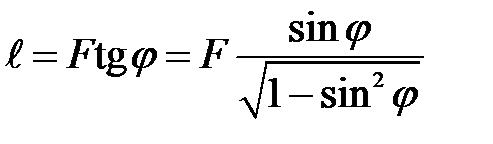 (25)
(25)
Подставив значение 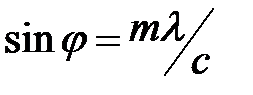 , получим
, получим
 L = F
L = F  (26)
(26)
ДИСПЕРСИЯ И РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ ДИФРАКЦИОННОЙ РЕШЕТКИ
Основные характеристики дифракционной решетки – ее дисперсия и разрешающая сила. Различают угловую и линейную дисперсии решетки. Угловой дисперсий называется величина, определяющая скорость изменения угла дифракции в зависимости от длины волны:
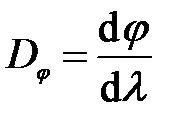 (27)
(27)
Продифференцировав выражение (16), получим:
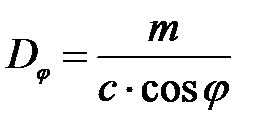 (28)
(28)
Для небольших углов 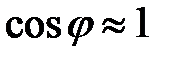 , следовательно:
, следовательно:
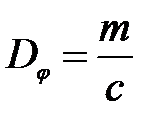 (29)
(29)
Линейной дисперсией называют величину, определяющую скорость изменения линейных размеров дифракционной картины в зависимости от длины волны:
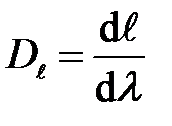 (30)
(30)
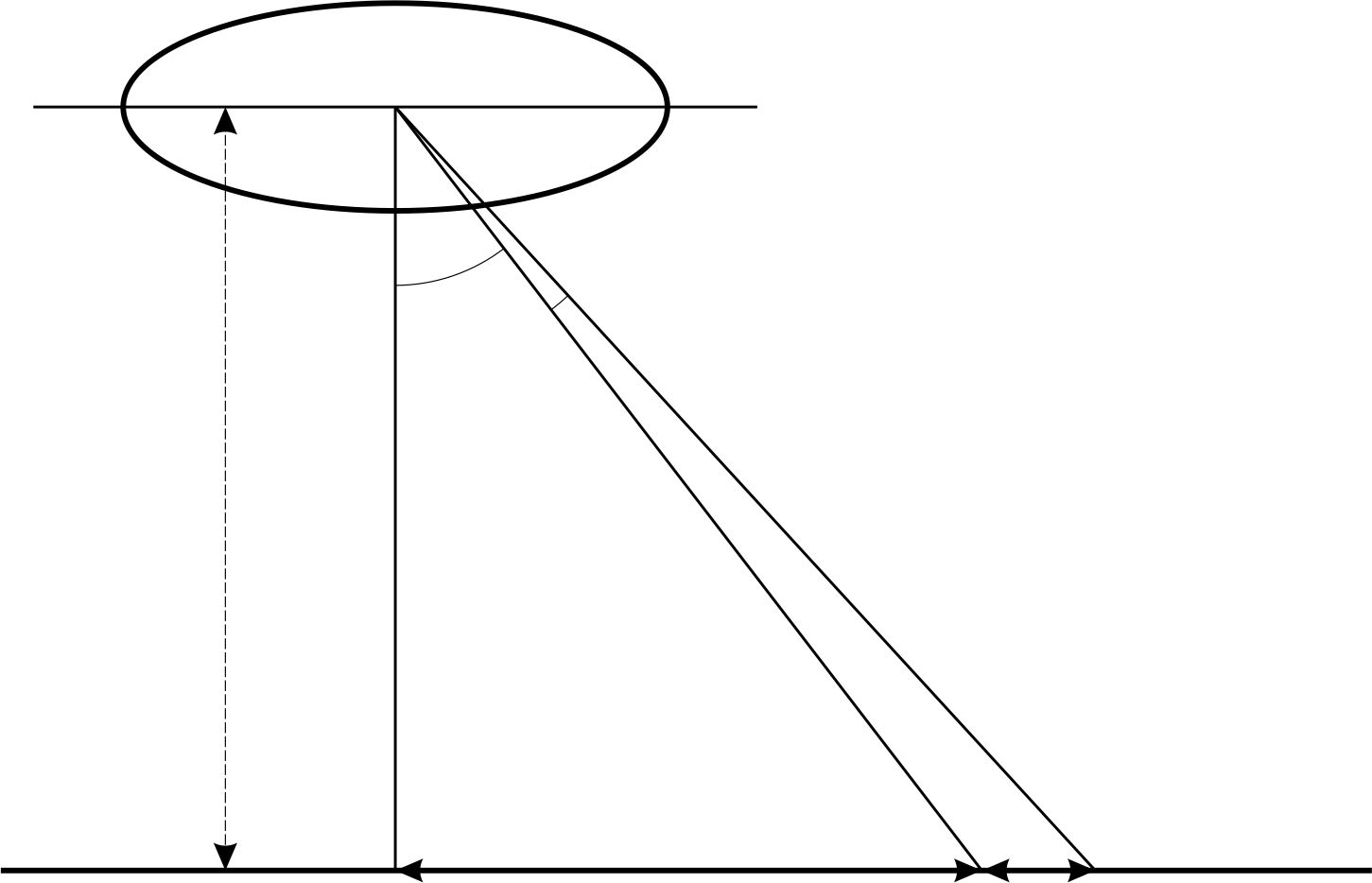
Из рис.6 видно, что при небольших углах 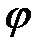
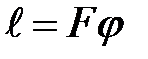 . Дифференцируя это выражение, получим:
. Дифференцируя это выражение, получим:
 (31)
(31)
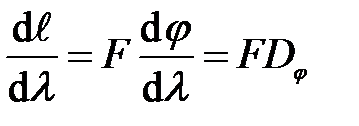 (32)
(32)
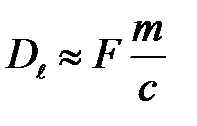 (33)
(33)
При спектральном разложении света с помощью дифракционной решетки каждая монохроматическая компонента будет представлена в виде дифракционной картины, главные максимумы которой будут сдвинуты относительно друг друга в соответствии с условием (16).
|

|
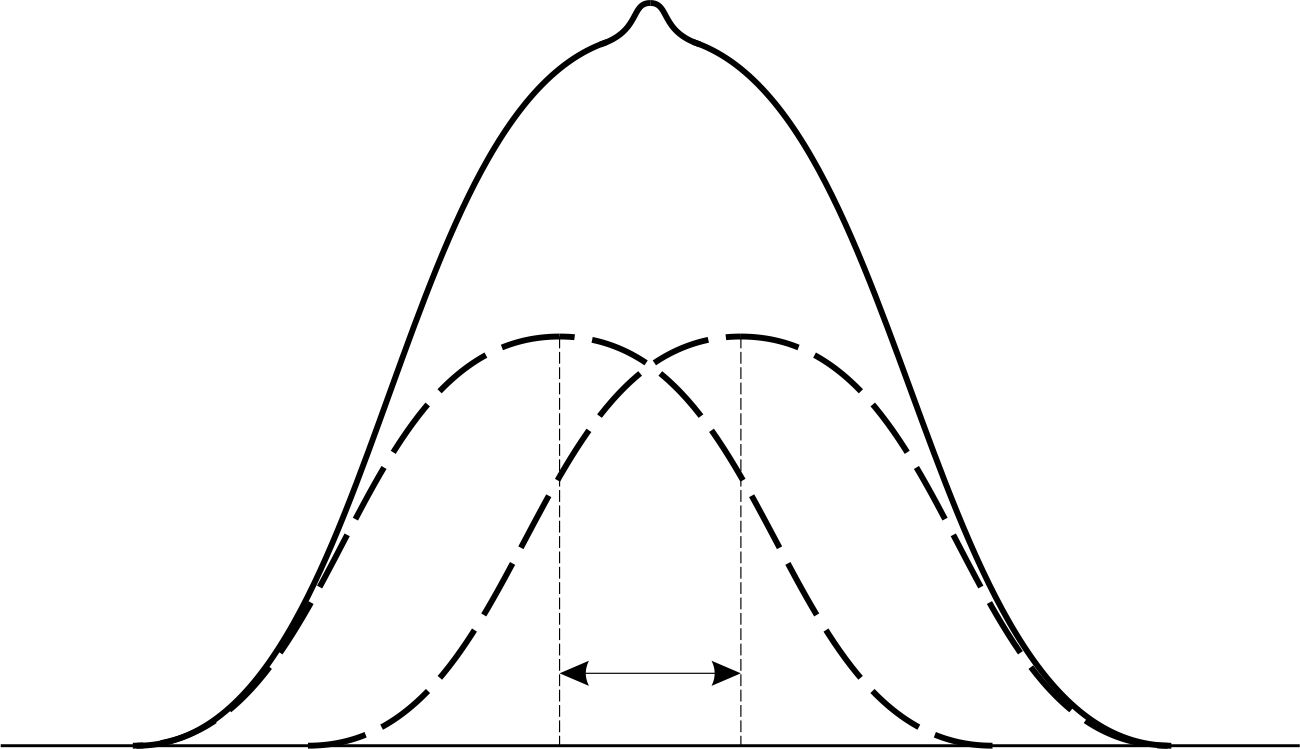
Рис. 6. Рис. 7.
Таким образом, в m-ном порядке спектра каждой монохроматической компоненте будет соответствовать свой дифракционный максимум. Возможность разрешения, т.е. раздельного восприятия на экране двух близких спектральных линий, зависит не только от расстояния между ними, которое определяется дисперсией прибора, но и от ширины спектрального максимума.
На рис.7 показано результирующее распределение интенсивности (сплошные кривые), наблюдающееся при наложении двух близких максимумов (пунктирные кривые). В случае а) оба максимума воспринимаются как один, в случае б) - раздельно.
Согласно критерию Релея, спектральные линии считаются полностью разрешенными, если середина одного максимума совпадает с краем соседнего (рис.7 б). В этом случае провал между максимумами составляет около 20%.
Разрешающей силой дифракционной решетки называется безразмерная величина.
Здесь 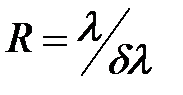 – разрешенный интервал, удовлетворяющий критерию Релея
– разрешенный интервал, удовлетворяющий критерию Релея
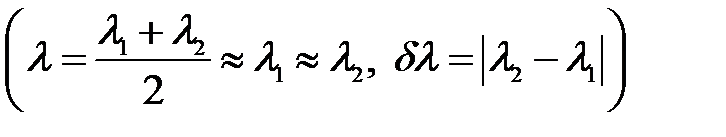 (35)
(35)
Положение середины 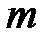 -го максимума для
-го максимума для 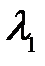 определяется условием
определяется условием
 (36)
(36)
Края 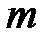 -го максимума для
-го максимума для  расположены под углами
расположены под углами
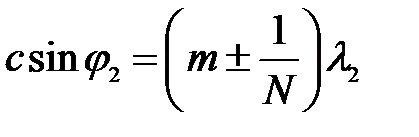 (37)
(37)
Середина максимума для длины волны 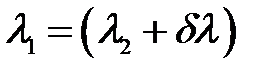 совпадет с краем
совпадет с краем
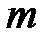 -го вторичного минимума для
-го вторичного минимума для  в том случае, если
в том случае, если  , т.е.
, т.е.
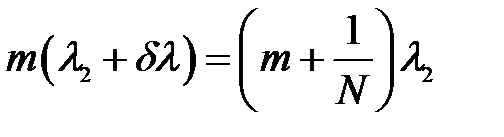 (38)
(38)
Откуда 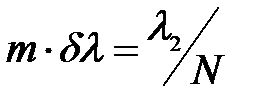 . Учитывая, что
. Учитывая, что 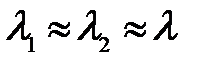 получим:
получим:
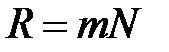 . (39)
. (39)
Таким образом, разрешающая способность тем больше, чем выше порядок спектра 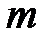 и чем больше число штрихов
и чем больше число штрихов 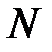 .
.
Методика и техника эксперимента
Для изучения дифракции в параллельных лучах применяется установка, изображенная на рис.8.

|
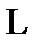
|
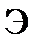
|
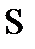
|
Рис. 8.
Свет от источника монохроматического излучения  падает на щель
падает на щель 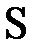 , фокусируется в фокальной плоскости линзы
, фокусируется в фокальной плоскости линзы 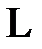 и рассматривается на экране
и рассматривается на экране 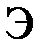 . Дифракционная картина, обусловлена дифракцией Фраунгофера, возникающей при прохождении параллельного пучка света через щель
. Дифракционная картина, обусловлена дифракцией Фраунгофера, возникающей при прохождении параллельного пучка света через щель 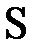 .
.
Порядок выполнения работы:
I.Дифракции от одной щели
1. Произвести тщательную юстировку всей установки, добиваясь, чтобы в поле зрения микроскопа получилось резкое изображена щели коллиматора (исследуемые щели при этом должны быть сняты).
2. Изучению подлежит пространственное распределение максимумов и минимумов наблюдаемых дифракционных картин. Приступая к наблюдению дифракции, нужно иметь в виду следующие обстоятельства.
· Во-первых, при наблюдении дифракции на объекте с малым числом целей резко уменьшается световой поток, попадающий в объектив.
· Во-вторых, может оказаться, что при наблюдении дифракционной картины от одной узкой щели, или от небольшого числа щелей, деления окулярного микрометра будут плохо заметны на фоне дифракционной картины. В таком случае нужно временно выдвинуть рамку со светофильтром и, пользуясь дифракционной картиной в белом свете, навести перекрестие на середину центрального максимума. После этого, поставив на место светофильтр, уже нетрудно заметить деление микрометра, совпадающие с близлежащими минимумами. Все наблюдения дифракционной картины вследствие малой интенсивности нужно вести в затемненной комнате, исключив попадание света от посторонних источников.
· В-третьих, нужно иметь в виду, что резкость дифракционной картины никогда, по самому существу дела, не может быть такой же, как у изображения щели коллиматора при его прямом попадании в трубу микроскопа. Поэтому, наблюдая дифракционную картину в параллельных лучах, бессмысленно пытаться «получше их сфокусировать», если микроскоп предварительно был сфокусирован на ясное видение щели микроскопа.
3. Поместив соответствующий рейтер с раздвижной щелью, провести несколько раз качественные наблюдения дифракционной картины в красном свете, изменяя ширину раздвижной щели. Следует начинать с широкой щели, когда видна многолинейчатая дифракционная картина, и уменьшая ширину щели, заканчивать, когда в поле зрения окуляра виден только один широкий и слабый дифракционный максимум.
4. Измерить ширину центрального дифракционного максимума для 3-х различных ширин щели, и, пользуясь формулой (12), вычислить ширины щели 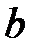 . Результаты измерений и вычислений занести в таблицу 1:
. Результаты измерений и вычислений занести в таблицу 1:
Таблица 1.
| № | 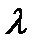 , м , м
| 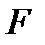 , м , м
|  , дел , дел
|  , м , м
| 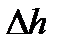 , м , м
|  , м , м
| 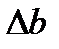 , м , м
|
| 1. 2. 3. 4. 5. |
II.Дифракция от многих щелей
1. Заменить красный светофильтр на зеленый.
2. Помещая на пути луча поочередно решетки с пятью и пятнадцатью щелями, пронаблюдать изменение дифракционной картины с изменением числа щелей. Результаты объяснить в отчете.
3. Измерить расстояние 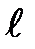 от центрального максимума до первого, определив его как полусумму расстояний между первым правым и первым левым максимумом. Пользуясь формулой (26) вычислить длину волны света, пропускаемого в максимуме светофильтра.
от центрального максимума до первого, определив его как полусумму расстояний между первым правым и первым левым максимумом. Пользуясь формулой (26) вычислить длину волны света, пропускаемого в максимуме светофильтра.
4. Вычислить угловую, линейную дисперсии, а также разрешающую способность в первом и втором порядках исследуемых решеток.
Результаты измерений и вычислений занести в таблицу 2.
Таблица 2.
| № | 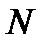
|  , , 
| 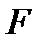 ,м ,м
| 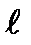 , дел , дел
| 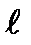 , м , м
| 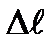 , м , м
| 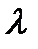 , м , м
| 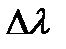 , м , м
|  , м-1 , м-1
|  , м , м
| 
| 
|
| 1. 2. 3. 4. 5. |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. В чем заключается принцип Гюйгенса-Френеля?
2. Определить явление дифракции. В чем различие дифракции Френеля и дифракции Фраунгофера?
3. Вывести условие максимумов и минимумов при дифракции на одной щели.
4. Почему при освещении щели или решетки «белым» светом главный максимум остается «белым», тогда как вся дифракционная картина цветной?
5. В чем отличие дифракционной картины, даваемой одной щелью и дифракционной решеткой?
6. Что называется угловой, линейной дисперсией, разрешающей способностью дифракционной решетки? Отчего зависят эти параметры?
7. Что произойдет на экране, если перемещать перпендикулярно оптической оси линзу, решетку?
ЛИТЕРАТУРА
1. Ландсберг Г.С. Оптика, М., Наука, 1976, с. 150 – 234.
2. Калитеевский Н.И. Волновая оптика. М., Высшая школа,