Представим себе, что мы работники Animal Planet и хотим изучить траекторию движения в джунглях какой-нибудь редкой змейки из красной книги. Назовем, например, изучаемую змею Зигзагусс.

С целью исследования мест обитания змеи и ее повадок цепляем к ее хвосту GPS-датчик, который будет регистрировать ее местоположение в отдельные моменты времени.

Вопрос: как надо запрограммировать датчик, чтобы мы получили точную траекторию движения змейки, т.е. получили самый подробный график траектории движения юркой змейки со всеми ее виляниями и изгибами? Через сколько миллисекунд или секунд датчику необходимо будет записывать и посылать нам очередную координату положения в пространстве?

Допустим, наша змея Зигзагусс ползет гармонично – ее хвост совершает гармонические колебания и ее движения можно описать синусоидальными функциями.

Фото настоящего следа от змеи на песке.
Траектория движения представляет собой колебания с различными частотами. Так вот, по правилам теоремы о дискретизации, чтобы восстановить всю траекторию движения змейки, необходимо найти составляющую колебаний самой высокой частоты.

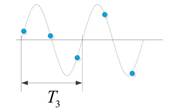
Если по дискретным точкам мы сможем восстановить составляющую колебаний самой высокой частоты, то мы сможем восстановить всю траекторию змейки. Определим периоды всех колебаний (см. рисунок ниже).

Как видно из рисунка, наименьшим периодом колебаний является период. Следовательно, необходимо подобрать частоту выборки дискретных точек именно для колебания с периодом, тогда и все остальные колебания мы сможем потом восстановить. Другими словами, в соответствии с теоремой о дискретизации можно полностью восстановить данную синусоидальную функцию, если брать дискретные точки через интервал времени вдвое меньший длительности периода. Это означает, что необходимо брать точки с таким интервалом, чтобы на период колебания самой высокой частоты приходилось не менее 2-х точек.
В этом случае можно будет с высокой точностью восстановить всю непрерывную траекторию движения исследуемой змеи.
Предположим теперь, что Зигзагусс опьянилась запахом одурманивающего цветка и стала ползти негармонично, несуразно.

В этом случае для определения периода дискретизации нам необходимо самим отыскать гармонию в данной кривой функции, а она есть внутри любого сигнала всегда, что пытался в свое время доказать всем людям французский математик Жан-Батист Фурье. Также как любое тело можно разложить на множество атомов, также и полученную сложную функцию (от траектории змеи), можно разложить на множество гармонических функций. Физические тела разные, потому что они отличаются друг от друга структурой молекул. Например, мы говорим H2O – это вода, что означает: молекула воды состоит из двух атомов водорода H и одного атома кислорода O. Точно также можно сказать, что разные сигналы отличаются разным составом. Например, такой вот сигнал

состоит из двух гармонических функций (синус и косинус) с частотой 1000 Гц и одного синуса с частотой 2000 Гц (2000 Гц означает, что гармоника совершает 2 тысячи колебаний в секунду). В соответствии с условием теоремы Котельникова, о котором мы уже ранее говорили, для такого сигнала временной интервал между дискретными точками необходимо брать таким, чтобы он был меньше половины периода самой высокой частоты. В нашем случае имеется гармоника с максимальной частотой 2 тысячи колебаний в секунду (2000 Гц), значит период сигнала равен 1/2000 = 0.005 секунд и значит период между дискретными точками должен быть менее, чем 0.005/2 = 0.0025 секунды.
Чтобы определить требуемый период между дискретными точками для траектории нашей змейки, необходимо определить из каких гармонических функций она состоит, а точнее нас интересует значение частоты наивысшей гармонической функции (т.е. фиолетовой на рисунке).

Делим период фиолетовой гармоники пополам, и получаем граничное значение для периода дискретизации функции траектории одурманенной змеи. Все, задача решена, можно произвести дискретизацию данного сложного сигнала.