Физический смысл производной.

Производная функции.

 

2.1 Определение производной функции одной переменной.

Пусть на некотором отрезке X=[a;b] определена функция f(x). Возьмем любую точку х Î Х и зададим аргументу х в данной точке произвольное приращение ∆х такое, что точка х +∆х так же принадлежит Х. Этим значениям аргумента х и х+∆х соответствуют следующие значения функции:

y(х) = f(х)

у(х+∆х) = f(х+∆х).

Приращение аргумента равно ∆х.

Приращение функции ∆y = f(х+∆х)-f(х).

Производной функции f(х) в точке х называется предел отношения приращения ∆y функции к при­ращению аргумента ∆х, когда приращение аргумента стремится к нулю:

=

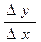
Для обозначения производной функции используют символ

y '(х) или f ′(х).

 

Читается: y'(х) - «иг­рек штрих по х »,

f '(х) - «эф штрих по х ».

Таким образом, по определению:

f ′(х) = =

Замечание 1: Предел

должен существовать (т.е. быть конечным), только тогда можно говорить, что функция имеет производную в данной точке.

Случай, когда = ∞ в данной работе не рассматривается.

Замечание 2: ∆y и ∆х — это единые символы, поэтому в выражении на ∆ сократить нельзя.

Процесс нахождения производной называется диффе­ренцированием функции. Функция называется дифферен­цируемойв точке х, если ее приращение можно представить в виде:

 

∆y=y'∆х + αΔх,

где y' – производная функции f(х) в точке х,

α = α(х) —бесконечно малая при Δх→0, т.е.

 

lim α = 0

^Dx®0

Дифференциалом функции y = f(х) в точке х называ­ется главная часть приращения функции в этой точке

 

dy = f'΄(х)Δх.

 

Дифференциалом независимой переменной х по определению считается величина: dх=Δх. Тогда дифференцил функции равен

 

dy = f΄(х)dх.

 

Таким образом:

 

 

Из данной формулы следует другое определение производной:

 

Производная есть отношение дифференциала функции

К дифференциалу аргумента.

Формула для дифференциала функции очень важна при взятии интегралов, приближенного вычисления функции в данной точке и решении дифференциальных уравнений.

 

 

Геометрический смысл производной.

Пусть функция y=f(х) определена на отрезке X=[a;b] и пусть точка М на графике функции соответствует значению аргумента х, а точка Р значению х+∆х (смотри Рис.1). Проведем через точку М и Р прямую и назовем ее секущей (S₁). Значение функции в точках М и Р

равно f(х) и f(х+∆х) соответственно. Из рассмотрения Рис. 1 видно, что тангенс угла наклона секущей S₁ равен

 

Касательной S к графику функции y=f(х) в точке М (х;у) будем называть предельное положение секущейМР(S₁) при Р→М‚ т.е. при Δх→0.

 

 

 

 

f(x+Dx)

 

 

f(x)

 

Рис. 1.

Производная функции y=f(х) в точке х равна угловому коэффициенту касательной к графику функции y=f(х) в точке М (х;f(х)) = М(х,y):

 

f'^΄(х) = tg φ₀ =

Физический смысл производной.

Пусть функция s=s(t) описывает закон движения материальной точки М по прямой траектории, т.е. s=s(t) — путь, пройденный точкой М от начала отсчета за время t. Тогда путь, пройденный М за время t + ∆t равен f(t + ∆t). За промежуток времени ∆t тело М пройдет путь, равный

∆s= s(t + ∆t) —s(t).

 

Средняя скорость Vср. движения точки М на отрезке ∆у за время ∆t равна:

Vср= ∆s/∆t.

Предел данного отношения при ∆t→ 0 называется мгновенной скоростью движения тела М в момент времени t:

По определению это и есть производная функции s=s(t) в точке t, т. е. производная функции s=s(t) в момент времени t есть мгновенная скорость тела М в данной точке.