Занятие №73-74.
Тема: Перпендикуляр и наклонные. Угол между прямой и плоскостью.
Цель: Сформировать понятие проекции наклонной на плоскость, расстояния между точкой и плоскостью и угла между прямой и плоскостью.
Ход занятия.
ü 1. Что изучаем:
ü
ü Определение перпендикуляра, наклонной и проекции наклонной на плоскость; расстояние от точки до плоскости.
Доказательство теоремы о трех перпендикулярах;
Определение угла между прямой и плоскость
Теоретический материал для самостоятельного изучения
Рассмотрим плоскость α и точку А, не лежащую в этой плоскости (рис. 1). Проведем через точку А прямую, перпендикулярную к плоскости α, и обозначим буквой Н точку пересечения этой прямой с плоскостью α. Отрезок АН называется перпендикуляром, проведенным из точки А к плоскости α, а точка Н — основанием перпендикуляра. Отметим в плоскости α какую-нибудь точку М, отличную от Н, и проведем отрезок AM. Он называется наклонной, проведенной из точки А к плоскости α, а точка М – основанием наклонной. Отрезок НМ называется проекцией наклонной на плоскость α.
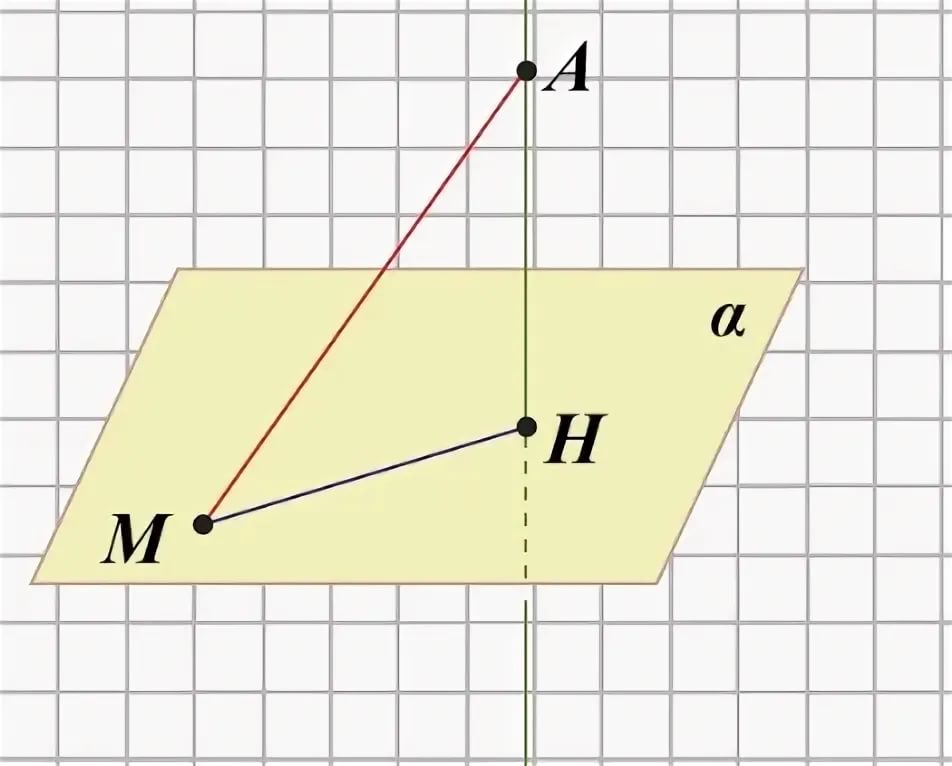

(Рис. 1)
Рассмотрим прямоугольный треугольник АМН. Сторона АН — катет, а сторона AM — гипотенуза, поэтому АН < AM. Поэтому перпендикуляр, проведенный из данной точки к плоскости, меньше любой наклонной, проведенной из той же точки к этой плоскости.
Следовательно, из всех расстояний от точки А до различных точек плоскости α наименьшим является расстояние до точки Н. Это расстояние, т. е. длина перпендикуляра, проведенного из точки А к плоскости α, называется расстоянием от точки А до плоскости α.
Сформулируем теорему о трех перпендикулярах:
Теорема: Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.


(Рис. 2)
На рисунке 2: АН — перпендикуляр к плоскости α, AM — наклонная, а — прямая, проведенная в плоскости α через точку М перпендикулярно к проекции наклонной НМ. Докажем, что прямая а перпендикулярна наклонной AM.
Рассмотрим плоскость АМН. Прямая а перпендикулярна к НМ по условию. Так как прямая а, лежит в плоскости α, а эта плоскость перпендикулярна отрезку AH, то прямая а перпендикулярна к этой плоскости. Отсюда следует, что прямая а перпендикулярна к любой прямой, лежащей в плоскости АМН, в частности прямая а перпендикулярна отрезку АМ. Теорема доказана.
Эта теорема называется теоремой о трех перпендикулярах, так как в ней говорится о связи между тремя перпендикулярами АН, НМ и AM.
Справедлива также обратная теорема: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.
Введем теперь понятие проекции произвольной фигуры на плоскость. Проекцией точки на плоскость называется основание перпендикуляра, проведенного из этой точки к плоскости, если точка не лежит в плоскости, и сама точка, если она лежит в плоскости.
Обозначим буквой F какую-нибудь фигуру в пространстве. Если мы построим проекции всех точек этой фигуры на данную плоскость, то получим фигуру F1, которая называется проекцией фигуры F на данную плоскость (рис. 3).
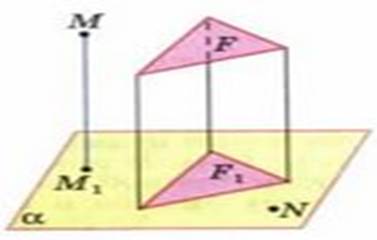

(Рис. 3)
Докажем теперь, что проекцией прямой на плоскость, не перпендикулярную к этой прямой, является прямая (рис. 4).
Данную плоскость обозначим буквой α. Произвольную прямую, не перпендикулярную к плоскости, обозначим буквой а. Из какой-нибудь точки М прямой а проведем перпендикуляр МН к плоскости αи рассмотрим плоскость β, проходящую через прямую a и перпендикуляр МН. Плоскости α и β пересекаются по некоторой прямой а1.
Докажем, что эта прямая и является проекцией прямой а на плоскость α. В самом деле, возьмем произвольную точку М 1 прямой а и проведем в плоскости β прямую М1Н1, параллельную прямой МН.
Так как отрезок MH перпендикуляр к плоскости α и отрезок MH параллелен М1Н1, то отрезок М1Н1 тоже перпендикулярен плоскости α.
Этим мы доказали, что проекция произвольной точки прямой а лежит на прямой а1.
Аналогично доказывается, что любая точка прямой а1 является проекцией некоторой точки прямой а. Следовательно, прямая а1 — проекция прямой а на плоскость α. Что и требовалось доказать.
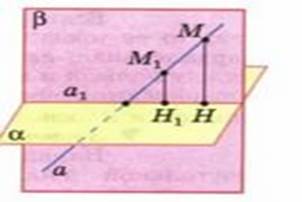

(Рис. 4)
Теперь введем понятие угла между прямой и плоскостью.