Числовые последоват и ряды и их предел
Если кажд натур числу n  поставлено соотв число xn, то множ-во занумерованных чисел х1,х2,х3….хn наз числ-й послед-ю (хn)=x1,x2,..
поставлено соотв число xn, то множ-во занумерованных чисел х1,х2,х3….хn наз числ-й послед-ю (хn)=x1,x2,..
Отдельные числа хn наз членами послед-и, а член хn наз общим членом послед-и.
Послед-ть есть ф-я, отображающая мн-во натур-х чисел n в мн-во дейст-х чисел R.
Если дана послед-ть хn и из некот-го бесконеч-го подм-ва ее членов образована новая послед-ть, порядок следования кот-й такойже, то она наз подпослед-ю этой послед-ти.
Число а наз пределом послед-ти хn при n  и обозн
и обозн  n, если для люб полож-го сколь угодно малого числа сущ такой норер, зависячий от
n, если для люб полож-го сколь угодно малого числа сущ такой норер, зависячий от  , что для всех номеров n больше или равно n выпол нерав
, что для всех номеров n больше или равно n выпол нерав  n
n 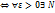 e
e  n
n  e
e  n-a
n-a 
Числ послед-ть, имеющ-я пред-л наз сходящейся, а послед кот-я пред-а не имеет наз расход-ся.
Числ послед хn наз бескон-но боль-й, если для люб сколь угодно боль-го полжит числа М  сущ такой номер
сущ такой номер  , что для всех номеров боль-х чем М вып нерав
, что для всех номеров боль-х чем М вып нерав  n|
n| 
Послед-ть 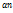 наз бескон-о мал-й числ посл-ю, если
наз бескон-о мал-й числ посл-ю, если  , т. е. для люб сколь угодно мал-о чи-а сущ такой номер
, т. е. для люб сколь угодно мал-о чи-а сущ такой номер  , что для всех ном больш либ равн-х вып нерав
, что для всех ном больш либ равн-х вып нерав
Св-ва БМП
1.суммаа конеч-го числа БМ чисел послед есть БМ числ послед-ть
2.произвед-е огранич-й послед-ти на БМ-ю есть БМ-я послед-ть
3.произвед-е конеч-о числа БМП-ти есть БМП-ть
4.если (хn)-ББП, то 1/хn - БМП
Если 
5.числ послед хn имеет пред-л число а, тогда и т. т., когда ее можно представ виде хn=а+  , где
, где 
Св-ва сход послед-ти
1.сход послед имеет единств пред-л
2.всякая подпосл-ть сходящ-я послед-ти сход-ся к тому же пред-лу
3.сход послед-ть ограничена
4.если пред-л послед  n равен а
n равен а  , то начин с некот номера имеет тот же знак, что и число а
, то начин с некот номера имеет тот же знак, что и число а
5.если пред-л послед  n равен а, уn=в и а
n равен а, уn=в и а 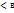 ,то начин-я с некот номера
,то начин-я с некот номера  n будет
n будет  уn
уn
6.если  n=а, уn=в, пред-л
n=а, уn=в, пред-л  n рав а, пред-л уn рав в и нач с некот номера
n рав а, пред-л уn рав в и нач с некот номера  n
n  уn, то а
уn, то а 
7.теорема о трех послед. Пусть для 3-х послед-й  n,уn, zn вып нерав
n,уn, zn вып нерав  n
n  ,уn
,уn  , zn и пред-лы послед-й совпад-т и равны некот числу а, тогда пред-л,уn будет равн-ся этому числу а
, zn и пред-лы послед-й совпад-т и равны некот числу а, тогда пред-л,уn будет равн-ся этому числу а
Теорема 1. Правила нахожд пред-ов послед-й. если послед  n,уn сходятся их пред-ы рвны соответств а и в, то пред-л суммы последоват равен сумме пред-ов этх послед-й
n,уn сходятся их пред-ы рвны соответств а и в, то пред-л суммы последоват равен сумме пред-ов этх послед-й
1.
2.
3.
4.
5.
Числовые ряды
Числовым рядом наз.выражение ввида ∑∞п=1 un=u1+u2+…+un+… ---(1) где u1,u2.,un—действительные числа, которые наз.членами рядов, un-общий член ряда.
Сумма 1-ых n-рядов наз.n-частичной суммой рядом (1) и обозн. Sn= u1+u2+…+un если сущест.конечный предел S=  n –(2) то говорят что ряд (1) сходится и этот предел наз.суммой ряда (1).Если предел (2) не сущ. Или равен ∞ то ряд (1) наз.расходящимся, такой ряд суммы не имеет.
n –(2) то говорят что ряд (1) сходится и этот предел наз.суммой ряда (1).Если предел (2) не сущ. Или равен ∞ то ряд (1) наз.расходящимся, такой ряд суммы не имеет.
Св-ва:
1)если ряд (1) сходится и его сумма равна S то ряд  , с-некоторое не нулевое действ.число, также сходится и его сумма равна c*S
, с-некоторое не нулевое действ.число, также сходится и его сумма равна c*S
2)если сходится ряд (1) и сходится ряд 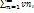 сумма ряда (1) =S1,а второго =S2.
сумма ряда (1) =S1,а второго =S2.  и его сумма равна S= S1+ S2.
и его сумма равна S= S1+ S2.
3)если к ряду (1) добавить или отнять конечное число членов, то полученный ряд и ряд (1) сходится или расход.одновременно.
Необходимо признак сходим.ряда.
Теорема1: Если ряд(1) сходится, то общий член этого ряда un стремится к нулю при n→∞.

Достаточные признаки сходимости знаков постоянных рядов в общим случаи не предостовляется возможности установить сход или расход. Поэтому сход и расход устанавл с помощью достаточных признаков сход рядов.
Теорема(признак сравнения): Пусть даны 2ряда  –(1) и
–(1) и  -(2) если выполнены неравенство un=vn то из сход ряда(2) след расход ряда(1) а из расход ряда(1) след сход ряда(2).
-(2) если выполнены неравенство un=vn то из сход ряда(2) след расход ряда(1) а из расход ряда(1) след сход ряда(2).
Теорема(второй признак) Пусть даны 2 положител ряда (1) и (2) если сущ конечный отличный от нуля  то ряды (1) и (2) сход или расход одновременно.
то ряды (1) и (2) сход или расход одновременно.
Теорема (признак Даламбера) Пусть дан ряд (1) с положител членами и сущ конечный или бесконечный предел  тогда ряд(1) сход при
тогда ряд(1) сход при  1 расход
1 расход  используем другой признак.
используем другой признак.
Теорема(радикальный признак Коши) Пусть дан ряд (1) с положит членами и сущ конечн или бесконечн предел  =
=  тогда при
тогда при  1 расход
1 расход  используем другой признак.
используем другой признак.
Функция 1. Множества
Множ-ом наз. Совокупность объектов 1-ой природы (А,В,С..)
Объекты, принадл-е множ-ву(образующие это множ0во) наз. Элементами множ-ва (а,в,с) аϵА – элем-т принадл-т множ-ву А;
Множ-во, кот-е не содержит элементов наз. Пустым.
Мн-во А наз. Подмн-ом мн-ва В, если каждый элем-т мн-ва А явл. Элемен-ом мн-ва В.
Мн-во А и В наз. Равными или совпадают, если мн-во А явл. Подмн-ом мн-ва В.
Объединение мн-в А и В наз. Мн-во, сост-е из тех элем-ов, кот-е принадлеж-т хотябы 1-му из тих мн-в.
Пересечение мн-в А и В наз мн-во сост. Из элем-ов каждый из кот-х принадлежит одновременно и мн-ву А и мн-ву В.
2. числовые промежутки.
Числ. Промежут-ми наз.подмн-ва мн-ва действительных чисел.
Пусть х0 ϵ R (действит. Число)
Окрестностью т. х0 наз. Любой интервал ав, содержащий т. х0. В частности интервал х0 наз. Эпсилон( -окрестностью х0
-окрестностью х0
, где х0 наз центром интервала, а положит. Число  (эпсилон) наз его радиусом.
(эпсилон) наз его радиусом.
Понятие функции
Пусть даны 2 мн-ва соответств. f, кот-е каждого элем-та х ставит соответств-е 1-н предмет У наз. функ-й у=f(x)  . при этом х наз. Областью определения ф-и (f) от мн-ва х.
. при этом х наз. Областью определения ф-и (f) от мн-ва х.
Способы задания
Ф-ю можн. Задать графически, в виде таблицы, формулы.
Пусть задана ф-я f x  , если элем-ми мн-ва Х и У явл. Действит. Числа, то задана числовая ф-я.
, если элем-ми мн-ва Х и У явл. Действит. Числа, то задана числовая ф-я.
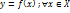 при этом переменная х наз. Независимой перемен-й, а у зависимой перемен. Или ф-ей. Относительно перемен-х х и у говорят, что они наход. В функц. Зависим-ти.
при этом переменная х наз. Независимой перемен-й, а у зависимой перемен. Или ф-ей. Относительно перемен-х х и у говорят, что они наход. В функц. Зависим-ти.
Графиком ф-и  наз. Мн-во всех точек плоскости оху, для каж-ой из кот-х х явл. Значением аргумента, а у – соотв. Значением ф-и.
наз. Мн-во всех точек плоскости оху, для каж-ой из кот-х х явл. Значением аргумента, а у – соотв. Значением ф-и.
Осн. Хар-ки ф-и
1.Ф-я  наз. Четной, если выполн. Усл.
наз. Четной, если выполн. Усл. 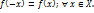 ф-я
ф-я 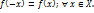 нах. Нечетной, если выполн. Усл.
нах. Нечетной, если выполн. Усл. 
2.Ф-я 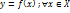 и мн-во
и мн-во  1
1  , если для люб-х знач-й аргумента
, если для люб-х знач-й аргумента  1, х2 ϵ
1, х2 ϵ  1 из неравенства
1 из неравенства  1˂ х2
1˂ х2  f(x1)˂f(x2), то ф-я f наз возрастающей на мн-ве
f(x1)˂f(x2), то ф-я f наз возрастающей на мн-ве  1, если же из нерав.
1, если же из нерав.  1˂ х2
1˂ х2  f(x1)≤f(x2), то ф-я (f) наз неубывающей на мн-ве
f(x1)≤f(x2), то ф-я (f) наз неубывающей на мн-ве  1. Если из неравен.
1. Если из неравен.  1˂ х2
1˂ х2  f(x1)>f(x2), то ф-я (f) наз убывающей на мн-ве D1. Если же из нерав.
f(x1)>f(x2), то ф-я (f) наз убывающей на мн-ве D1. Если же из нерав.  1˂ х2
1˂ х2  f(x1)≥f(x2), то ф-я (f) наз невозрастающей на мн-ве
f(x1)≥f(x2), то ф-я (f) наз невозрастающей на мн-ве  1. Возраст-е, невозраст-е, убыв-е, неубыв-е ф-и на мн-ве
1. Возраст-е, невозраст-е, убыв-е, неубыв-е ф-и на мн-ве  1 наз монотонными на этом мн-ве. Возраст-е и убыв-е ф-и наз строго монотоннами
1 наз монотонными на этом мн-ве. Возраст-е и убыв-е ф-и наз строго монотоннами
Числ. Промежутки, на кот-х ф-я монотонна наз промежутками монотон-ти ф-и.
3.Ф-я 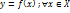 наз ограниченной на мн-ве
наз ограниченной на мн-ве  , если сущ. Такое положит-е число М, что для всех х из мн-ва
, если сущ. Такое положит-е число М, что для всех х из мн-ва  выполн. Неравенство
выполн. Неравенство  . Отсюда следует, что график огранич-й ф-и распологается между горизонт. Прямыми.
. Отсюда следует, что график огранич-й ф-и распологается между горизонт. Прямыми.
4.Периодичность. Ф-я 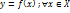 наз периодической на этом мн-ве, если сущ такое положит число Т, что для люб-го
наз периодической на этом мн-ве, если сущ такое положит число Т, что для люб-го  при этом Т наз периодом ф-и (f)
при этом Т наз периодом ф-и (f)
Обратная ф-я
Рассм ф-ю 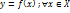 с мн-ом значений
с мн-ом значений  , если каждому знач-ю
, если каждому знач-ю  из мн-ва
из мн-ва  соотв-т единствен-е знач-е
соотв-т единствен-е знач-е  , то определена ф-я
, то определена ф-я  и мн-ам знач-й X такая ф-я
и мн-ам знач-й X такая ф-я  наз обратной ф-и
наз обратной ф-и  и запис. В виде x=f-1(y)=
и запис. В виде x=f-1(y)=  . из опред-я обрат-й ф-и след-т, что ф-я имеет обрат-ю тогда и т. т., когда эта ф-я задает взаимно однозначное соотв-е между мн-ом определения и мн-ом значения. Люб-я строго монотонная ф-я имеет обратную.
. из опред-я обрат-й ф-и след-т, что ф-я имеет обрат-ю тогда и т. т., когда эта ф-я задает взаимно однозначное соотв-е между мн-ом определения и мн-ом значения. Люб-я строго монотонная ф-я имеет обратную.
Осн элементарные ф-и и их графики
1. Показательная ф-я
У=ах а>0 а  1
1
а>1 
 0˂а˂1
0˂а˂1
Степенная ф-я
у=х2

у=х3

у=х-1
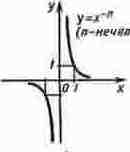
у=х1

Логарифмическая ф-я

а>0

0˂а˂1

Тришонометрические ф-и
y =sin x, y =cos x, y = tg x, y = ctg x.
Обратные тригоном ф-и
y=arcsinx, y=arccos x, y = arctg x, y = arcctg x.