Прямая МВ перпендикулярна к сторонам АВ и ВС треугольника АВС. Определите вид треугольника МВD, где точка D – произвольная точка прямой АС.

Занятие №15-16.

Тема: Признак перпендикулярности прямой и плоскости.

Цель: Научиться применять признак перпендикулярности прямой и плоскости при решении стереометрических задач.

Ход занятия.

Повторение ранее изученного материала

ü Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90º.

ü Прямая называется перпендикулярной к плоскости, если она перпендикулярная к любой прямой, лежащей в этой плоскости.

ü Лемма о перпендикулярности двух прямых к третьей прямой: если одна из двух параллельных прямых перпендикулярная к третьей прямой, то и другая прямая перпендикулярна к этой прямой.

ü Теорема о параллельных прямых, перпендикулярных плоскости: если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.

ü Признак перпендикулярности прямой и плоскости: если прямая перпендикулярная к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

2. Теоретический материал для самостоятельного изучения

Для того чтобы проверить перпендикулярность прямой к плоскости достаточно проверить перпендикулярность лишь к двум пересекающимся прямым, лежащим в этой плоскости.

Для доказательства рассмотрим прямую a, перпендикулярная к прямым p и q, лежащим в плоскости α и пересекающимся в точке О.

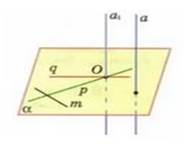
На рисунке видно, что прямая может проходить как через точку О, так и через произвольную точку плоскости. Прямая m – произвольная прямая, лежащая в плоскости α и для того, чтобы доказать, что прямая а⊥α, необходимо доказать, что прямая а⊥m. Дальнейшее доказательство теоремы опустим.

3. Примеры.

Пример 1.

Докажем, что прямые CA₁ и BD, проходящие через вершины куба ABCDA₁B₁C₁D₁, перпендикулярны

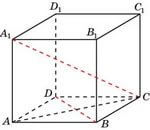
Рассмотрим плоскость ACC₁ и прямую BD. Так как прямая BD перпендикулярна прямым AA₁ и AC, то по признаку перпендикулярности прямой и плоскости, прямая BD перпендикулярна ACC₁.

Следовательно, прямая BD перпендикулярна любой прямой в ACC₁. В частности, прямая BD перпендикулярна прямой CA₁. Что и требовалось доказать.

Пример 2.

Верно ли, что если прямая перпендикулярна каким-нибудь двум прямым плоскости, то она перпендикулярна этой плоскости?

Решение. Воспользуемся признаком перпендикулярности прямой и плоскости: если прямая перпендикулярная к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости. В нем сказано, что прямые в плоскости должны пересекаться. В условии подобного не сказано, поэтому утверждение неверно.

Ответ: неверно.

Пример 3.

Треугольник АВС – равносторонний, CD – медиана, MD перпендикулярно плоскости ABC. AB = 2√3, MD = 4. Найти MC.

Решение. Рассмотрим треугольник ABC. Он равносторонний. Это означает, что его медиана так же является высотой и биссектрисой. Рассмотрим треугольник ADC. Он прямоугольный, т.к. DC - медиана и высота. Сторона AD равна √3. По теореме Пифагора вычислим длину стороны DC:

DC=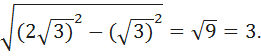

Далее рассмотрим треугольник MDC, он прямоугольный, т.к. MD перпендикулярна плоскости ABC. Воспользовавшись теоремой Пифагора, найдем MC:

МС= = = .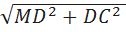

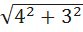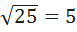Ответ: 5.

Домашняя работа

Задача 1.

Прямая АВ параллельна плоскости α (альфа). Через точки А и В проведены прямые, перпендикулярные к плоскости α, которые пересекают эту плоскость в точках 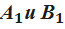соответственно. Докажите, что АВ=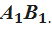

Задача 2.

Прямая МВ перпендикулярна к сторонам АВ и ВС треугольника АВС. Определите вид треугольника МВD, где точка D – произвольная точка прямой АС.