Частные производные высших порядков

Частные производные

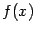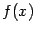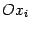Пусть -- внутренняя точка области , и в области задана функция . Рассмотрим ограничение функции на прямую , проходящую через точку параллельно оси . Эта прямая задаётся условиями при ; переменная 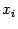может при этом произвольно меняться. Поэтому для рассматриваемого ограничения имеется естественная параметризация, смысл которой в том, что "замораживаются" все переменные, от которых зависит 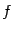, кроме :

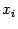Получили функцию одного переменного , как параметризацию ограничения с помощью параметра .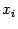

Рис.7.12.

Функция может иметь производную в точке , равную некоторому числу 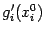. Это число называют частной производной функции 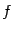по переменной 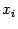, вычисленной в точке . Эта частная производная обозначается или .

Сразу же заметим, что значения частных производных от функции 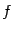в точке , вычисленные по разным переменным 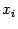и 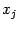, могут быть различными, так что обозначение типа , без указания переменной, по которой вычислена частная производная, не имеет смысла: в обозначении обязательно нужно указывать переменную, по которой мы дифференцируем.

Итак, чтобы вычислить частную производную от функции 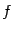по некоторой переменной 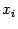, нужно фиксировать значения всех переменных, кроме 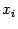(то есть временно считать их постоянными), а затем по обычным правилам вычисления производных найти производную по этой единственной переменной 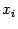. Теперь ясно, что для вычисления частных производных никаких новых правил дифференцирования вдобавок к тем, что известны нам для функций одной переменной, не потребуется, ведь при вычислении частной производной мы считаем, что может изменяться только одна переменная.

Считая точку , в которой вычисляется значение частной производной , переменной точкой области и предполагая, что во всех точках эта производная существует, мы получаем, что частная производная 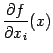-- это функция, заданная в области (или в её части, если производная существует не везде в ).

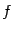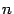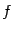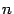Поскольку частную производную функции можно вычислять по каждой из переменных , то функция имеет частных производных

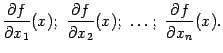
Эти частные производные, вообще говоря, -- различные функции. Их называют также частными производными первого порядка от функции 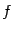. Итак, функция 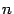переменных имеет 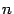частных производных первого порядка.

Пример 7.11 Вычислим частные производные функции двух переменных

по каждой из переменных и .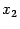

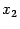Производную по найдём, считая переменной, а постоянной величиной:

При этом мы воспользовались тем, что производная суммы равна сумме производных, тем, что производная от (по ) равна 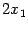, тем, что производная от (по , при постоянном значении ) равна , тем, что производная от (по ) равна 3, и, наконец, тем, что производная постоянного слагаемого равняется 0.

Аналогично найдём производную по переменной 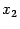. При этом мы считаем, что -- постоянная, а меняется только 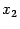, по которой мы и находим производную:

При этом слагаемые и постоянны, и их производная по 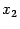равна 0; в слагаемом множитель постоянный, и его можно вынести за знак производной, а производная от равна 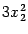; наконец, производная от равняется .

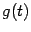В соответствии с изученным в первом семестре смыслом производной функции одного переменного (напомним, что производная функции равна скорости изменения значений функции 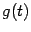в точке ), cмысл частной производной -- это скорость изменения значений функции 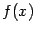при равномерном движении с единичной скоростью через точку по прямой , параллельной оси .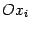

Геометрический смысл частной производной также становится ясен, если рассмотреть ограничение функции 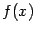, полученное при фиксации значений всех переменных, кроме 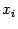. Для наглядности ограничимся случаем функции двух переменных и 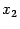. В этом случае мы можем изобразить график функции на чертеже в виде некоторой поверхности.

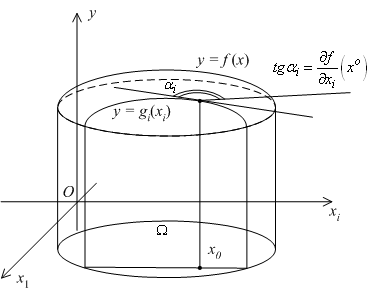
Рис.7.13.

Отметим на плоскости точку , в которой вычисляется частная производная 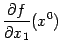, и рассмотрим сечение графика вертикальной плоскостью ; она проходит на плоскости через прямую , заданную тем же уравнением . Тогда эта плоскость высекает в поверхности графика линию, служащую графиком функции 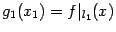. Функция -- это функция одной переменной , и её производная в точке 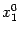равна тангенсу угла наклона касательной, проведённой к графику в точке 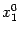. С другой стороны, 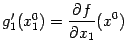. Значит, частная производная 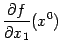имеет геометрический смысл как тангенс угла наклона касательной к сечению графика вертикальной плоскостью .

Точно так же, частная производная имеет геометрический смысл как тангенс угла наклона касательной к сечению графика вертикальной плоскостью 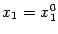. Заметим, что плоскост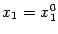и и взаимно перпендикулярны.

Если функция одного переменного имеет производную в некоторой точке, то эта функция обязательно непрерывна в этой точке; этот факт мы изучили в первом семестре. В случае нескольких переменных () дело обстоит не так. Даже наличия в некоторой точке частных производных функции 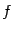по всем переменным не достаточно для того, чтобы функция была непрерывной в точке . Приведём пример такой функции двух переменных, что частные производные её сушествуют, а функция, тем не менее, разрывна.

Пример 7.12 Рассмотрим функцию, заданную при :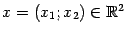

Эта функция разрывна в точке , поскольку в любой, как угодно малой окрестности начала координат имеются точки вида , где , в которых значение функции равно

а также точки вида , где , в которых значение функции равно

а значение равно 0.

Однако ограничение функции 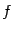как на прямую 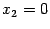, так и на прямую , проходящие через начало координат, тождественно равно 0:

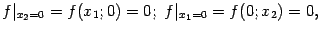
так что и производные от этих ограничений в точке 0 равны 0, то есть

Итак, обе частные производные в начале координат существуют, но функция разрывна в начале координат.

Частные производные высших порядков

Мы уже заметили, что частные производные первого порядка 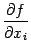мы можем рассматривать, в предположении их существования, как функции, заданные в некоторой области пространства 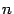переменных . От каждой из этих функций 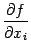, в свою очередь, можно найти частные производные: 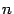производных от :

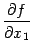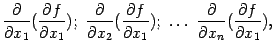
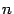производных от :

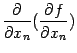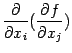и так далее до ; всего получается производных где . Производная обозначается также или . Эти производные называются частными производными второго порядка от функции .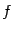

Если , то есть если второе дифференцирование ведётся по той же переменной 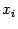, что и первое, то частная производная второго порядка называется чистой частной производной второго порядка по переменной 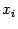и более кратко обозначается .

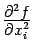Если же 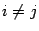, то частная производная второго порядка называется смешанной частной производной второго порядка.

Итак, для функции 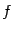можно отыскать 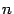чистых частных производных второго порядка и смешанных. Ниже мы увидим, что при некоторых дополнительных предположениях смешанные частные производные и 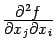, отличающиеся порядком дифференцирований, совпадают, так что различных смешанных производных второго порядка оказывается не , а вдвое меньше.

Пример 7.13 Пусть

Найдём частные производные второго порядка. Для этого сначала найдём производные первого порядка:

Затем находим производные от :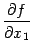

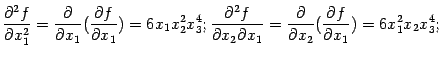
производные от :

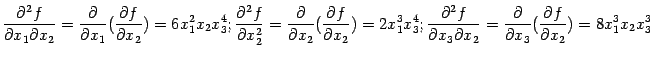
и производные от :

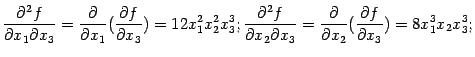
От любой из частных производных второго порядка можно рассматривать, в свою очередь, частные производные:

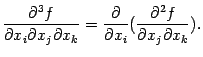
Эти производные (их штук) называются частными производными третьего порядка; от них можно найти частные производные четвёртого порядка

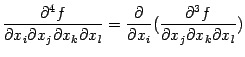
и т. д.

Если при вычислении частной производной высокого порядка некоторые дифференцирования проводятся по одной и той же переменной несколько раз подряд, то это отражается в обозначениях очевидным образом, например, 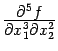означает то же самое, что

Пример 7.14 Вычислим 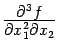для функции 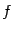из предыдущего примера.

Поскольку

имеем