13.11.20.
Классная работа.
Решение задач по теме «Метод координат».
План работы на уроке.
1. Выполните Тест по вариантам. Записывайте в каждом задании используемую формулу, решение и ответ. В заданиях 1-5 необходимо выбрать вариант ответа, в заданиях 6-9 получить ответ в ходе решения.
2. Запишите в тетради решение Дополнительной задачи.
3. Решите задачи для самостоятельной работы.
4. Домашнее задание: №973 (смотри решение задачи 972 учебника)
ВАРИАНТ 1.
По теме «Метод координат»
1. Координаты вектора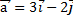 
равны: а) 
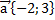б) 
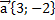в)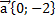 
2. Если А(3; 4) и В(-2;5), то вектор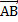 
имеет координаты: а) 
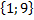б) 
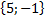в)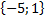 
3. Концы отрезка CD имеют координаты С(5;1) и D(3; - 7), тогда координаты точки М – середины отрезка CD: а) (- 2; 2) б) (4; -4) в) (4; - 3)
4. Точки А и В имеют координаты А (- 3; - 1) и В (2; - 4). Тогда расстояние между ними равно…..
а)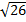 
б) 4 в)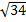 
5. Вектор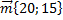 
имеет длину: а) 35 б) 5 в) 25
6. Даны точки А(2; 0), В(- 1; 3), С(4; 6). Тогда вектор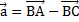 
имеет координаты ………..
7. Точка А (2; 3) – один из концов отрезка АВ. С (2; 1) – середина отрезка АВ. Тогда координаты точки В будут ………………………..
8. Длина медианы СМ треугольника АВС, вершины которого имеют координаты А (1; - 4),
В (5; 2) и С (0; 3) равна…………………..
9. Вершины треугольника АВС имеют координаты А (- 5; 6), В(3; – 9) и С (- 12; - 17)
Длины каких сторон равны? Найдите периметр треугольника.
Дополнительная задача.
Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Решение.
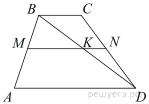
Введём обозначения, как показано на рисунке.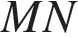 
— средняя линия, поэтому, 
откуда по теореме Фалеса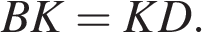 
Рассмотрим треугольник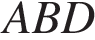 
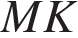— средняя линия, следовательно,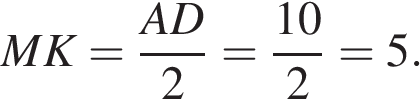 
Ответ: 5.
Самостоятельно решите задачи.
1. Основания трапеции равны 17 и 19. Найдите меньший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
2. Средняя линия трапеции равна 15, а большее основание равно 17. Найдите меньшее основание трапеции.
3. Основания трапеции равны 26 и 14. Найдите отрезок, соединяющий середины диагоналей трапеции.
ВАРИАНТ 2.
По теме «Метод координат»
1. Координаты вектора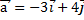 
равны: а) 
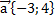б) 
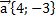в)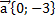 
2. Если А(-2; 4) и В(1;- 3), то вектор 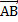имеет координаты: а) 
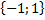б) 
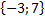в)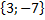 
3. Концы отрезка AB имеют координаты A(2;- 3) и B(- 4; 5). тогда координаты точки C – середины отрезка AB: а) (-2;2) б) (-1; 4) в) (- 1; 1)
4. Точки M и N имеют координаты M (3; - 2) и N (- 1; 3). Тогда расстояние между ними равно…..
а)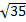 
б) 6 в)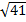 
5. Вектор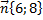 
имеет длину: а) 10 б) 14 в) 2
6. Даны точки А(2; 4), В(- 1; 3), С(0; 5). Тогда вектор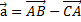 
имеет координаты ………..
7. Точка А (4; 5) – один из концов отрезка АВ. K (- 1; 4) – середина отрезка АВ. Тогда координаты точки В будут ………………………..
8. Длина медианы АМ треугольника АВС, вершины которого имеют координаты А (0; 1),
В (1; - 4) и С (5; 2) равна…………………..
9. Вершины треугольника АВС имеют координаты А (4; 8), В(12; 5) и С (7; 0)
Длины каких сторон равны? Найдите периметр треугольника.
Дополнительная задача.
Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Решение.
Введём обозначения, как показано на рисунке. 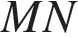— средняя линия, поэтому, откуда по теореме Фалеса 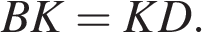Рассмотрим треугольник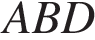 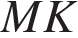— средняя линия, следовательно,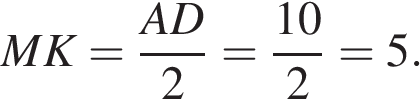
Ответ: 5.
Самостоятельно решите задачи.
1. Основания трапеции равны 16 и 17. Найдите меньший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
2. Средняя линия трапеции равна 11, а меньшее основание равно 5. Найдите большее основание трапеции.
3. Основания трапеции равны 14 и 19. Найдите отрезок, соединяющий середины диагоналей трапеции.