Понятие многогранника
Раздел геометрии, в котором изучаются свойства фигур в пространстве, называется стереометрией.
Это слово στερεομετρία происходит от древнегреческих слов «stereos» — объёмный, пространственный и «metria» — измерение.
Простейшие фигуры стереометрии — точки, прямые и плоскости. Из этих фигур образованы геометрические тела и их поверхности.
Если поверхности геометрических тел составлены из многоугольников, то такие тела называются многогранниками.
Многоугольники, из которых составлен многогранник, называются его гранями. При этом предполагается, что никакие две соседние грани многогранника не лежат в одной плоскости.
Стороны граней называются рёбрами, а концы рёбер — вершинами многогранника.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.
Многогранники бывают выпуклыми и невыпуклыми.

Выпуклый многогранник характеризуется тем, что он расположен по одну сторону от плоскости каждой своей грани. На рисунке выпуклый многогранник — октаэдр. У октаэдра восемь граней, все грани — правильные треугольники.

На рисунке — невыпуклый (вогнутый) многоугольник. Если рассмотреть, например, плоскость треугольника EDC, то, очевидно, часть многоугольника находится по одну сторону, а часть — по другую сторону этой плоскости.
Призма
Теперь можем ввести определение призмы.
n -угольной призмой называют многогранник, составленный из двух равных n -угольников, лежащих в параллельных плоскостях, и n -параллелограммов, которые образовались при соединении вершин n -угольников отрезками параллельных прямых.
Равные n-угольники называют основаниями призмы.
Стороны многоугольников называют рёбрами оснований.
Параллелограммы называют боковыми гранями призмы.
Параллельные отрезки называют боковыми рёбрами призмы.
Призмы бывают прямыми и наклонными.
Если основания прямой призмы — правильные многоугольники, то такую призму называют правильной.
У прямых призм все боковые грани — прямоугольники. Боковые рёбра прямой призмы перпендикулярны к плоскостям её оснований.
Если из любой точки одного основания провести перпендикуляр к другому основанию призмы, то этот перпендикуляр называют высотой призмы.
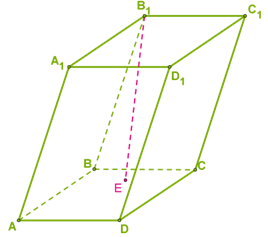
На рисунке — наклонная четырёхугольная призма, в которой проведена высота B1E.
В прямой призме каждое из боковых рёбер является высотой призмы.

На рисунке — прямая треугольная призма. Все боковые грани — прямоугольники, любое боковое ребро можно называть высотой призмы. У треугольной призмы нет диагоналей, так как все вершины соединены рёбрами.

На рисунке — правильная четырёхугольная призма. Основания призмы — квадраты. Все диагонали правильной четырёхугольной призмы равны, пересекаются в одной точке и делятся в этой точке пополам.
Четырёхугольная призма, основания которой — параллелограммы, называется параллелепипедом.
Вышеупомянутую правильную четырёхугольную призму можно также называть прямым параллелепипедом.
Если основания прямого параллелепипеда — прямоугольники, то этот параллелепипед — прямоугольный.

На рисунке — прямоугольный параллелепипед. Длины трёх рёбер с общей вершиной называют измерениями прямоугольного параллелепипеда.
Например, AB, AD и AA1 можно называть измерениями.
Так как треугольники ABC и ACC1 — прямоугольные, то, следовательно, квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов его измерений:
AC12=AB2+AD2+AA12.
Если через соответственные диагонали оснований провести сечение, получится то, что называют диагональным сечением призмы.
В прямых призмах диагональные сечения являются прямоугольниками. Через равные диагонали проходят равные диагональные сечения.
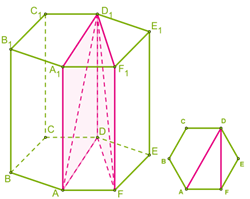
На рисунке — правильная шестиугольная призма, в которой проведены два разных диагональных сечения, которые проходят через диагонали с разными длинами.
Основные формулы для расчётов в прямых призмах
1. Боковая поверхность Sбок.=Pосн.⋅H, где H — высота призмы. Для наклонных призм площадь каждой боковой грани определяется отдельно.
2. Полная поверхность Sполн.=2⋅Sосн.+Sбок.. Эта формула справедлива для всех призм, не только для прямых.
3. Объём V=Sосн.⋅H. Эта формула справедлива для всех призм, не только для прямых.