Различают моментные и интервальные ряды динамики, ряды абсолютных, относительных и средних величин.
| Ряды динамики |
| По признаку времени |
| По виду статистического показателя |
| интервальные |
| моментные |
| ряды абсолютных величин |
| ряды относительных величин |
| ряды средних величин |
| с равными промежутками между датами |
| с неравными промежутками между датами |
Методы исчисления среднего уровня ряда динамики зависят от вида ряда динамики (рис. 9.2).
|
| Средний уровень ряда |
| интервальный ряд |
| моментный ряд |
| с равными промежутками между датами |
| с неравными промежутками между датами |
|
|
| полная информация на каждую дату |
|
Пример. Имеются данные об объеме продукции и основных фондов по организации:
| Показатель | Месяц | |||
| январь | февраль | март | апрель | |
| Объем продукции, тыс. руб. | ||||
| Стоимость основных фондов на начало месяца, тыс. руб. |
| Показатель | январь | март | апрель | июль |
| Объем незавершенного производства на начало месяца, тыс. руб. |
Следующий пункт задания №4 – выявление тенденции изучаемого явления.
Предлагается показать знание методов выявления тренда на примере данных об объеме реализации за последний пятый год по вашим данным, которые вы получили путем корректировки исходной информации по своей зачетной книжке. Мы возьмем данные из исходного примера.
А) Метод укрупнения интервалов. Необходимо перейти от месячных данных к средним показателям по кварталам года.
Расчётная таблица для определения укрупнённых (поквартальных) данных
| Месяцы | Объем реализации продукции, тыс. тонн | Кварталы | Объем реализации продукции за квартал, тыс. тонн | Среднемесячный объем реализации продукции, тыс. тонн | |
| январь | 2 435,0 | первый | 5421,0 | 1807,0 | |
| февраль | 1 375,1 | ||||
| март | 1 610,9 | ||||
| апрель | 2 211,6 | второй | 7612,6 | 2537,5 | |
| май | 2 563,1 | ||||
| июнь | 2 837,9 | ||||
| июль | 3 040,9 | третий | 9543,4 | 3181,1 | |
| август | 3 488,2 | ||||
| сентябрь | 3 014,3 | ||||
| октябрь | 2 637,7 | четвёртый | 7266,4 | 2422,1 | |
| ноябрь | 2 328,4 | ||||
| декабрь | 2 300,3 | ||||
| Итого | 29 843,4 | Итого | 29 843,4 | 2487,0 |
|
|
Вывод. Данные табл. 4.3 показывают, что в результате применения метода укрупнения интервалов проявилось общее направление (тренд) изменения объема реализации продукции: в первых трех кварталах среднемесячные объемы реализации продукции возрастали, а в четвертом существенно снизились.
Б) Метод скользящей средней.
Расчётная таблица для определения значений скользящей средней
| Месяцы | Объем реализации продукции, тыс. тонн | Скользящая трехзвенная сумма, тыс. тонн | Скользящая средняя, тыс. тонн |
| январь | 2 435,00 | - | - |
| февраль | 1 375,10 | 5 421,00 | 1807,0 |
| март | 1 610,90 | 5 197,60 | 1732,5 |
| апрель | 2 211,60 | 6 385,60 | 2128,5 |
| май | 2 563,10 | 7 612,60 | 2537,5 |
| июнь | 2 837,90 | 8 441,90 | 2814,0 |
| июль | 3 040,90 | 9 367,00 | 3122,3 |
| август | 3 488,20 | 9 543,40 | 3181,1 |
| сентябрь | 3 014,30 | 9 140,20 | 3046,7 |
| октябрь | 2 637,70 | 7 980,40 | 2660,1 |
| ноябрь | 2 328,40 | 7 266,40 | 2422,1 |
| декабрь | 2 300,30 | - | - |
| Итого | 29 843,4 | - | - |
Вывод. Как показывают данные табл.4.4, значения скользящей средней до сентября месяца почти систематически возрастали, а затем стали снижаться, что свидетельствует об общей параболической тенденции изменения объемов реализации продукции. Поскольку большая часть параболы близка к прямолинейной форме (7 значений скользящей средней из 10-ти систематически возрастают), для сглаживания ряда динамики может быть использовано выравнивание ряда по прямой (а не по параболе).
|
|
В) Метод аналитического выравнивания.
Линейное уравнение тренда имеет вид:
где t – порядковый номер периодов (или моментов) времени;
– выравненные значения ряда динамики.
Параметры линейного уравнения тренда определяются путем решения следующей системы нормальных уравнений:
Эту систему уравнений можно упростить, если ввести обозначение времени так, чтобы сумма показателей времени ряда динамики была равна нулю[1]: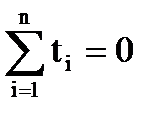 
При соблюдении этого принципа отсчёт а времени t система нормальных уравнений примет вид:
Тогда параметры можно определить по формулам:
, 
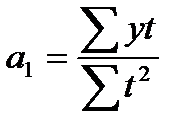
Расчет значений величин 
, 
и 
приведен ниже в таблице (графы 2, 4, 5)
Расчетная таблица для определения параметров 
уравнения прямой
| Месяц | Объем реализации, тыс. тонн,
| Условное обозначение периодов,
| 
| 
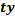
| Выровненные уровни ряда динамики,
тыс. тонн
|
| январь | 2 435,00 | -11 | -26785 | 2077,769231 | |
| февраль | 1 375,10 | -9 | -12375,9 | 2152,165734 | |
| март | 1 610,90 | -7 | -11276,3 | 2226,562238 | |
| апрель | 2 211,60 | -5 | -11058 | 2300,958741 | |
| май | 2 563,10 | -3 | -7689,3 | 2375,355245 | |
| июнь | 2 837,90 | -1 | -2837,9 | 2449,751748 | |
| июль | 3 040,90 | 3040,9 | 2524,148252 | ||
| август | 3 488,20 | 10464,6 | 2598,544755 | ||
| сентябрь | 3 014,30 | 15071,5 | 2672,941259 | ||
| октябрь | 2 637,70 | 18463,9 | 2747,337762 | ||
| ноябрь | 2 328,40 | 20955,6 | 2821,734266 | ||
| декабрь | 2 300,30 | 25303,3 | 2896,130769 | ||
| Итого | 29 843,40 | 21277,4 | 29843,40000 |
Параметры уравнения равны:
|
|
= 2486,95 
= 37,20
Уравнение прямой, характеризующее основную тенденцию развития явления, имеет вид: 
В графе 6 рассчитаны выравненные (теоретические) уровни ряда динамики на основе полученного уравнения:
· для января t = -11 
· для февраля t = -9 
· и т.д.
Сумма значений уровней эмпирического ряда (гр.2) должна совпадать с суммой значений уровней выровненного ряда (гр.6) или незначительно расходиться с ней.
В расчетах наблюдается совпадение сумм: 29 843,4 = 29 843,4
Графики эмпирической и сглаживающей кривых представлены на рис.4.2.
Рис. 4.2. Сглаживание ряда динамики объемов реализации продукции методом аналитического выравнивания по прямой
3. Следующий пункт задания №4 – прогнозирование значений показателя методами экстраполяции.
А) Прогнозирование уровня ряда динамики с использованием среднего абсолютного прироста осуществляется по следующей формуле:
где: 
– прогнозируемый уровень;
t – период упреждения (число лет, кварталов и т.п.);
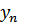– конечный уровень исследуемого ряда динамики;
– средний за исследуемый период абсолютный прирост (среднегодовой, среднеквартальный и т.п.).
Прогнозируемый объем реализации продукции на 7 год (по данным пятилетнего периода) с использованием среднего абсолютного прироста, рассчитанного в задании 4.2:
Вывод. Если средний абсолютный прирост в будущем останется на том же уровне, можно ожидать, что в 7-м году объем реализации составит 33972,8 тыс. тонн.
Б) Прогнозирование уровня ряда динамики с использованием среднего темпа (коэффициента) роста осуществляется по следующей формуле:
где 
– средний за исследуемый период темп роста (среднегодовой, среднеквартальный и т.п.).
Прогнозируемый объем реализации продукции на седьмой год (по данным пятилетнего периода) с использованием среднего темпа роста, рассчитанного в задании 2:
Вывод. Если средний темп роста в будущем останется на том же уровне, можно ожидать, что в 7-м году объем реализации составит 35067,7 тыс. тонн.
В). Прогнозирование объемов реализации продукции методом аналитического выравнивания ряда динамики.
Модель линейной зависимости уровня ряда от фактора времени, как мы уже отмечали, имеет следующий вид:
Ранее было показано, как определить параметр линейного уравнения тренда. Отмечалось, что систему уравнений можно упростить, если ввести обозначение времени так, чтобы сумма показателей времени ряда динамики была равна нулю. Но можно этого и не делать, а для обозначения периодов (моментов) времени использовать ряд натуральных чисел. В методических указаниях была предложена именно такой принцип обозначения периодов времени: для первого года t =1, для второго t =2 и т.д.
Вспомогательная таблица для расчёта параметров тренда
| год | Объем реализации, тыс. тонн,
| Условное обозначение периодов,
|
|
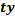
| Выровненные уровни ряда динамики,
тыс. тонн
| |
| 1-й | 21584,7 | 21584,7 | 20866,22 | |||
| 2-й | 22887,9 | 45775,8 | 22653,76 | |||
| 3-й | 23644,6 | 70933,8 | 24441,30 | |||
| 4-й | 24245,9 | 96983,6 | 26228,84 | |||
| 5-й | 29843,4 | 149217,0 | 28016,38 | |||
| Итого | 122206,5 | 384494,9 | 122206,5 |
122206,5
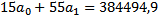
Решаем эту систему уравнений, определяем значение параметров 
и 
. Тогда уравнение тренда примет следующий вид:
Определим на его основе объем реализации продукции на 7 год (в принятой нами системе обозначения времени для этого года t =7):
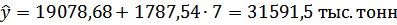
Вывод. Если выявленная тенденция изменения уровней ряда динамики сохранится в будущем, можно ожидать, что в 7-м году объем реализации составит 31591,5 
тыс. тонн.
4. Следующий пункт задания №4 – анализ сезонности развития явления.
Для выполнения этой части задания необходимо использовать скорректированные с учетом номера зачетной книжки данные за все пять лет.
Индекс сезонности (
) – отношение средней величины уровня, рассчитанной для каждого из 12 календарных месяцев за ряд лет (
), к среднемесячному уровню ряда динамики за весь рассматриваемый период (
), выраженное в процентах:
,
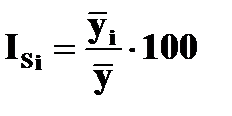где – средний уровень за i-й месяц года,
– среднемесячный уровень за весь пятилетний период данных.
Индексы сезонности могут исчисляться не только по месяцам, но по другим периодам времени: кварталам года, неделям месяца, дням недели.
Расчет удобно провести в таблице.
| Месяцы | 1 - й год | 2-й год | 3-й год | 4-й год | 5-й год | Среднемесячный объем реализации, тыс. тонн
| Индекс сезонности, %
|
| январь | 1 262,30 | 1 304,70 | 1 287,30 | 1 330,20 | 2 435,00 | 1523,9 | 74,8 |
| февраль | 1 250,70 | 1 324,00 | 1 300,70 | 1 340,30 | 1 375,10 | 1318,16 | 64,7 |
| март | 1 612,00 | 1 589,00 | 1 577,30 | 1 620,10 | 1 610,90 | 1601,86 | 78,6 |
| апрель | 1 950,00 | 2 088,70 | 2 061,30 | 2 150,50 | 2 211,60 | 2092,42 | 102,7 |
| май | 2 350,80 | 2 440,70 | 2 450,70 | 2 500,60 | 2 563,10 | 2461,18 | 120,8 |
| июнь | 2 628,00 | 2 989,30 | 2 706,70 | 2 755,80 | 2 837,90 | 2783,54 | 136,7 |
| июль | 2 606,00 | 2 961,30 | 3 920,00 | 3 980,00 | 3 040,90 | 3301,64 | 162,1 |
| август | 2 178,20 | 2 367,60 | 2 368,70 | 2 420,10 | 3 488,20 | 2564,56 | 125,9 |
| сентябрь | 1 857,30 | 1 879,30 | 1 928,70 | 1 980,20 | 3 014,30 | 2131,96 | 104,7 |
| октябрь | 1 544,00 | 1 553,30 | 1 580,50 | 1 620,90 | 2 637,70 | 1787,28 | 87,8 |
| ноябрь | 1 200,70 | 1 218,00 | 1 220,00 | 1 267,40 | 2 328,40 | 1446,9 | 71,0 |
| декабрь | 1 144,70 | 1 172,00 | 1 242,70 | 1 279,80 | 2 300,30 | 1427,9 | 70,1 |
| Итого | 21 584,70 | 22 887,90 | 23 644,60 | 24 245,90 | 29 843,4 | 122 206,5/60= 2036,77 | - |
На основании полученных индексов сезонности строится график сезонной волны, которыйнаглядно демонстрирует наличие сезонной компоненты в реализации продукции.
Вывод. В динамике объемов реализации продукции явно прослеживается наличие сезонной компоненты. Наибольшие объемы реализации продукции приходятся обычно на июль. Средний месячный объем реализации в этом месяце составляет 3301,64 тыс. тонн или 162,1% от годового среднемесячного уровня. Наименьшими объемами продаж отличается февраль. Объем реализации в этом месяце составляет в среднем 1318,16 тыс. тонн или 64,7% от годового среднемесячного уровня.
Рис.4.3. Сезонная волна динамики объемов реализации за пятилетний период
Далее требуется определить, каким можно ожидать ежемесячный объем реализации в 6-м году с учетом сезонных колебаний этого показателя, если годовой объем реализации в этом году составит 36 000 тыс. тонн (каждый студент это число должен для себя определить самостоятельно по указанному правилу).
Для этого сначала надо определить средний месячный уровень объема реализации в 6-м году:
На основе индексов сезонности имеем:
· январь составляет 74,8% от среднего месячного уровня
3000*0,748=2244,6
· февраль составляет 64,7%
3000*0,647=1941,5
и т.д.
Расчеты удобно проводить в таблице