Продукции на 6-ой год по индексам сезонности
| Месяц | Индекс сезонности, %

| Прогнозные оценки помесячной реализации продукции на 6-ой год, тыс. тонн

|
| январь | 74,8 | 2244,6 |
| февраль | 64,7 | 1941,5 |
| март | 78,6 | 2359,4 |
| апрель | 102,7 | 3082,0 |
| май | 120,8 | 3625,1 |
| июнь | 136,7 | 4099,9 |
| июль | 162,1 | 4863,0 |
| август | 125,9 | 3777,4 |
| сентябрь | 104,7 | 3140,2 |
| октябрь | 87,8 | 2632,5 |
| ноябрь | 71,0 | 2131,2 |
| декабрь | 70,1 | 2103,2 |
| Итого | - |
Задание 5
Пятое задание предполагает, что вы знаете индексный метод.
Исходные данные (которые должны быть изменены по определенным правилам каждым студентом)
| Форма торговли | Объем продаж, тыс.кг | Цена за 1 кг | ||
| III квартал | IV квартал | III квартал | VI квартал | |
| Сетевая | ||||
| Несетевая |
Требуется определить:
1. Индивидуальные индексы. Их общая формула построения:

 значение показателя в базисном периоде (или его плановый, нормативный уровень)
значение показателя в базисном периоде (или его плановый, нормативный уровень)
 значение показателя в отчетном периоде
значение показателя в отчетном периоде
Соответственно, используя принятые в теории индексов обозначения, можно записать формулы следующих показателей:
· индивидуальный индекс цен
 ,
,
где p0 и p1 – цена товара в базисном и отчетном периодах
· индивидуальный индекс физического объема
 ,
,
где q0 и q1 – цена товара в базисном и отчетном периодах
Расчет индивидуальных индексов цен:
- сетевая торговля: 
- несетевая торговля:  166,7%
166,7%
Вывод. В сетевой торговле цена на товар «А » выросла в IV кв. по сравнению с III кв. на 75% (175-100), что в абсолютном выражении составляет 30 руб.(70-40), в несетевой - на 67% или на 20 рублей.
Расчет индивидуальных индексов физического объема по формуле (5.2):
- сетевая торговля: 
- несетевая торговля: 
Вывод. В сетевой торговле объем продажи товара «А» вырос в IV кв. по сравнению с III кв. на 25% (125-100), что в абсолютном выражении составляет 1000 кг, в несетевой - на 20% или на 1000 кг.
2. Общие агрегатные индексы.
Основной формой построения общих индексов является агрегатная форма:
| Формула агрегатного индекса |

|
| Для качественных показателей (цена или себестоимость единицы товара, заработная плата, урожайность, трудоемкость и др.) |

|
| Для количественных показателей (количество продукции, численность сотрудников, посевная площадь и др.) |

|
Для расчета общих индексов удобно использовать следующую таблицу
Расчетная таблица
| Форма торговли | Объем продажи, тыс. кг | Цена товара, руб. | Товарооборот, тыс. руб. | ||||
| базисный период | отчетный период | базисный период | отчетный период | базисный период | отчетный период | отчетный период по ценам базисного периода | |

| 
| 
| 
| 
| 
| 
| |
| 6=2∙4 | 7=3∙5 | 8=3∙4 | |||||
| сетевая | |||||||
| несетевая | |||||||
| Итого | - | - |
Общий индекс цен характеризует:
· среднее относительное изменение цен;
· относительное изменение товарооборота под влиянием изменения цен
Исчисляется по формуле


Вывод. В целом по двум формам торговли цена товара выросла в IV кв. по сравнению с III кв. в среднем на 71,1%. Абсолютная сумма перерасхода денежных средств населения в результате повышения цены товара "А" составляет 270 тыс. руб. (650 - 380).
Общий индекс физического объема продаж показывает
· среднее относительное изменение количества проданных товаров;
· относительное изменение товарооборота под влиянием изменения объема продаж
Исчисляется по формуле

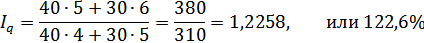
Вывод. В целом по двум формам торговли объем продаж товара увеличился
в IV кв. по сравнению с III кв. в среднем на 22,6%.
Общий индекс товарооборота характеризует относительное изменение товарооборота под влиянием двух факторов – изменения цен и физического объема продаж. Рассчитывается по формуле


Вывод: в целом по двум формам торговли товарооборот в IV кв. по сравнению с III кв. в результате изменения цен и физического объема продаж увеличился на 109,7 %, что в абсолютном выражении составляет 340 тыс. руб.
Для общих индексов, как и для индивидуальных, действует следующее правило: индексы связаны между собой так же, как и индексируемые величины. Например, товарооборот (выручка от реализации товаров) – это произведения цены на количество реализованного товара. Точно такая же зависимость выполняется для общих и индивидуальных индексов этих показателей:


Эта формула называется факторной моделью индекса товарооборота. Она показывает изменение товарооборота за счёт изменения цен и за счёт изменения объема продаж.

Вывод. В целом по двум формам торговли увеличение товарооборота в 2,097 раза произошло за счет роста цен в 1,711 раза и роста объема продаж в 1,226 раза.
Следующее задание: определение абсолютного изменения товарооборота -общего и в результате влияния отдельных факторов (изменения цен и изменения количества проданных товаров).
Общее абсолютное изменение товарооборота в отчетном периоде по сравнению с базисным (под влиянием двух факторов):


Легко видеть, что эта величина равнаразностимежду числителем и знаменателем индекса товарооборота.
Абсолютное изменение товарооборота в результате изменения цен:


Эта величина равнаразностимежду числителем и знаменателем общего индекса цен. Этот результат можно прокомментировать иначе, с точки зрения не продавца. а покупателя: перерасход денежных средств покупателей в результате повышения цены товара "А" на 71,1% составляет 270 тыс. руб.
Абсолютное изменение товарооборота в результате изменения физического объема продаж:


Легко видеть, что эта величина равнаразностимежду числителем и знаменателем индекса физического объема товарооборота.
Общее абсолютное изменение товарооборота в отчетном периоде по сравнению с базисным под влиянием двух факторов равно сумме двух приростов:


Вывод. В целом по двум формам торговли товарооборот в IV кв. по сравнению с III кв. под влиянием изменения цены товара (на 71,1%) вырос в среднем на 270 тыс. рублей. Рост физического объема продаж на 22,6% привел к увеличению товарооборота в среднем на 270 тыс. рублей. Совместное влияние двух факторов выразилось в росте общего объема товарооборота на 340 тыс. рублей или на 109,7%.
Следующее задание связано с анализом изменения средней цены товара. Поскольку товар один, но он продается в разными организациями по различным ценам, можно поставить задачу рассчитать среднюю цену товара и проанализировать ее изменение в динамике. Для этих целей используются индексы цен переменного состава, постоянного состава и влияния структурных сдвигов.
Вначале определяется средняя цена товара по формуле:

III кв. 
IV кв. 
Относительное изменение средней цены товара рассчитывается как отношение средней цены в отчетном периоде к средней цене в базисном периоде:
 (5.12)
(5.12)
или  (5.13)
(5.13)
Такой индекс называют индексом переменного состава, так как он отражает не только изменение уровня цен на товар (первый фактор), но и изменение в структуре объемов продажи, т.е. структурные сдвиги (второй фактор).
Расчет индекса цен переменного состава:
 , или 171,6%
, или 171,6%
Вывод. Средняя по двум формам торговли цена товара «А» в отчетном периоде по сравнению с базисным выросла на 71,6 % под влиянием роста цен и объемов продажи.
Для выявления влияния каждого фактора в отдельности на изменение средней цены рассчитывают еще два индекса – индекс цен постоянного (фиксированного) состава и индекс структурных сдвигов.
Влияние первого фактора (без учета влияния второго фактора – структурных сдвигов) отражает индекс фиксированного состава, характеризующий относительное изменение средней цены в структуре отчетного периода (т.е. IV кв.):
 , (5.14)
, (5.14)
или 
Расчет индекса фиксированного состава по формуле (5.14):

Вывод. Средняя по двум формам торговли цена товара в отчетном периоде по сравнению с базисным выросла на 71,1 % только под влиянием роста уровня цен по каждой форме торговли (в 1-й – на 75,0%, во 2-й – на 66,7%) без учета влияния структурных сдвигов.
Для характеристики относительного изменения средней цены товара под влиянием второго фактора (без учета влияния первого фактора – изменения уровня цен) рассчитывают индекс структурных сдвигов (Iстр .):

 (5.15)
(5.15)
Расчет индекса структурных сдвигов по формуле (5.15):

Вывод. Средняя (по двум формам торговли) цена товара «А» в отчетном периоде по сравнению с базисным выросла на 0,3% в результате структурных сдвигов в объемах продажи.
4.5. Индексы цен переменного, постоянного состава, индекс структурных сдвигов образуют систему взаимосвязанных индексов:


Вывод. При отсутствии структурного перераспределения в объеме продажи средняя цена товара по двум формам торговли возросла бы в 1,711 раза (или на 71,1%). Изменения в структуре объема продаж вызвали рост средней цены в 1,003 раза (или на 0,3%). Одновременное воздействие двух факторов (рост цен и структурные сдвиги в объемах продажи) привело к возрастанию средней цены товара в 1,716 раза (или на 71,6%)