ВОПРОСЫ
1. Что называется электрическим сигналом.
Сигнал - это любая физическая величина (например, температура, давление воздуха, интенсивность света, сила тока и т.д.), изменяющаяся со временем. Именно благодаря этому изменению сигнал может нести в себе какую-то информацию.
Электрические сигналы представляют собой электрические процессы, используемые для передачи, приема и преобразования информации.
Сигналы можно разделить на два больших класса: детерминированные и случайные. Детерминированными называются сигналы, мгновенные значения которых в любой момент времени можно предсказать с вероятностью, равной единице, и которые могут быть заданы в виде некоторой определенной функции времени
2. В чем суть спектрального анализа и какая разница между спектральным и частотным анализом.
Спектральный анализ – это один из методов обработки сигналов, который позволяет охарактеризовать частотный состав измеряемого сигнала. При помощи данного метода можно оценить спектральный состав сигнала, а также количественно выяснить его энергетические показатели. Преобразование Фурье является математической основой, которая связывает временной или пространственный сигнал (или же некоторую модель этого сигнала) с его представлением в частотной области.
Спектральный анализ – выделение энергетически значимых частот из бесконечного множества составляющих апериодического сигнала.
Частотный анализ на основе АЧХ.??? Частотный анализ – это спектральный анализ.
3. Что называется частотным спектром сигнала. Чем отличается частотный спектр периодического сигнала от частотного спектра непериодического сигнала.
Спектр сигнала это распределение энергии сигнала по частотам. Спектр бывает амплитудный и фазовый. Если известна форма сигнала (зависимость от времени), спектр может быть рассчитан при помощи преобразования Фурье. Для периодического сигнала ряд Фурье, для непериодического - интегральное преобразование.
Периодическим сигналом (током или напряжением) называют такой вид воздействия, когда форма сигнала повторяется через некоторый интервал времени T, который называется периодом. Простейшей формой периодического сигнала является гармонический сигнал или синусоида, которая характеризуется амплитудой, периодом и начальной фазой. Все остальные сигналыбудут негармоническими или несинусоидальными.
Амплитудный и фазовый спектры непериодического сигнала являются сплошными, в отличие от линейчатых спектров периодического сигнала.
Спектр периодического сигнала является дискретным и представляет набор гармонических колебаний, в сумме составляющий исходный сигнал.
Отметим следующие особенности спектра непериодической функции:
Спектр непериодического сигнала сплошной (непрерывный) и распространяется на отрицательные частоты.
1. Спектр непериодической функции времени непрерывен;
2. Область допустимых значений аргумента спектра
3.Действительная часть спектра – четная функция частоты, мнимая часть спектра – нечетная функция, что позволяет использовать одну половину спектра
При переходе к непериодическому сигналу мы получаем в спектре такого сигнала вместо отдельных гармоник бесконечно большое число синусоидальных колебаний с бесконечно близкими частотами, заполняющими всю шкалу частот. Причем амплитуда каждого такого колебания становится исчезающе малой, потому что на его долю приходится бесконечно малая часть энергии сигнала. Другими словами, в любой бесконечно узкой полосе частот мы всегда обнаружим синусоидальное колебание, правда, бесконечно малой амплитуды.
Поскольку сравнивать между собой бесконечно малые величины неудобно, то вместо амплитуд Ак по оси ординат – откладывают произведение Ак Т, которое с увеличением периода Т остается постоянным. Понятие спектра амплитуд здесь лишено смысла и заменяется понятием спектральной плотности амплитуд, которая указывает, по сути, на удельный вес бесконечно малой амплитуды синусоидального колебания в любой бесконечно узкой полосе частот. Понятие спектра фаз заменяется понятием спектральной плотности фаз.
4. Что называется спектральной плотностью и какой вид имеют сплошные АЧС и ФЧС.
Спектральная плотность характеристик сигнала - это распределение энергии или мощности сигнала по диапазону частот.
Совокупность частот образует частотный спектр сигнала (частотный состав), график в координатах (частота, амплитуда) называется амплитудно-частотным спектром сигнала (АЧС), а (частота, фаза) фазочастотным спектром сигнала (ФЧС).
Спектральная плотность мощности дает энергию сигнала на единицу полосы, т.е. на 1 Гц, поэтому и размерность у нее энергия на Герц.
АЧСпектр – это первая, где постепенное падение.
ФЧСпектр – вторая кривая синусоида.
5. Запишите в аналитической форме основные свойства преобразования Фурье (дифференцирование, интегрирование, запаздывание, смещение).
Смысл преобразования для электротехники - любой периодический сигнал можно разложить на гармонические составляющие (синусоиды разной фазы и амплитуды).
Первое из этих свойств — линейность. Если мы берем какую-то линейную комбинацию функций, то преобразование Фурье этой комбинации будет такой же линейной комбинацией образов Фурье этих функций. Это свойство позволяет сводить сложные функции и их фурье-образы к более простым. Например, фурье-образ синусоидальной функции с частотой f и амплитудой a является комбинацией из двух дельта-функций расположенных в точках f и -f и с коэффициентом a/2:
Если взять функцию, состоящую из суммы множества синусоид с разными частотами, то согласно свойству линейности, фурье-образ этой функции будет состоять из соответствующего набора дельта-функций. Это позволяет дать наивную, но наглядную интерпретацию спектра по принципу “если в спектре функции частоте f соответствует амплитуда a, то исходную функцию можно представить как сумму синусоид, одной из которых будет синусоида с частотой f и амплитудой 2a”. Строго говоря, эта интерпретация неверна, поскольку дельта-функция и точка на графике — это совершенно разные вещи, но как мы увидим дальше, для дискретных преобразований Фурье она будет не так уж и далека от истины.
Второе свойство преобразования Фурье — это независимость амплитудного спектра от сдвига сигнала по времени. Если мы подвинем функцию влево или вправо по оси x, то поменяется лишь её фазовый спектр.
Третье свойство — растяжение (сжатие) исходной функции по оси времени (x) пропорционально сжимает (растягивает) её фурье-образ по шкале частот (w). В частности, спектр сигнала конечной длительности всегда бесконечно широк и наоборот, спектр конечной ширины всегда соответствует сигналу неограниченной длительности.
Четвертое и пятое свойства самые, пожалуй, полезные из всех. Они позволяют свести свертку функций к поточечному перемножению их фурье-образов и наоборот — поточечное перемножение функций к свертке их фурье-образов. Чуть дальше я покажу насколько это удобно.
Шестое свойство говорит о симметрии фурье-образов. В частности, из этого свойства следует что в фурье-образе действительнозначной функции (т.е. любого “реального” сигнала) амплитудный спектр всегда является четной функцией, а фазовый спектр (если его привести к диапазону -pi...pi) — нечетной. Именно по этой причине на графиках спектров практически никогда не рисуют отрицательную часть спектра — для действительнозначных сигналов она не дает никакой новой информации (но, повторюсь, и нулевой при этом не является).
Наконец последнее, седьмое свойство, говорит о том, что преобразование Фурье сохраняет “энергию” сигнала. Оно осмысленно только для сигналов конечной продолжительности, энергия которых конечна, и говорит о том, что спектр подобных сигналов на бесконечности быстро приближается к нулю. Именно в силу этого свойства на графиках спектров как правило изображают только “основную” часть сигнала, несущую в себе львиную долю энергии — остальная часть графика просто стремится к нулю (но, опять же, нулем не является).
6. Дайте определение понятий «единичная ступенчатая функция» и «единичная импульсная функция». Опишите их свойства.
Единичная ступенчатая функция — специальная математическая функция, чьё значение равно нулю для отрицательных аргументов и единице для положительных аргументов.
Единичная импульсная функция равна нулю при всех значениях аргумента, отличных от нуля, но при нулевом значении аргумента она обращается в бесконечность.
Единичная импульсная функция является производной от единичной ступенчатой функции, а единичная ступенчатая функция-интегралом от единичной импульсной функции. Следовательно, вводится понятие производной от функции в точке ее разрыва.
Единичная импульсная функция - Реакция звена на единичный импульс
Единичная ступенчатая функция 1(t), называемая также функцией Хевисайда или функцией включения имеет значения:
и обычно неопределенна при t =0. График функции имеет вид
2) импульсная функция (δ–функция Дирака) (рис.11 б)
Импульсная функция представляет собой «идеальный импульс», ширина основания которого стремится к нулю, а высота – к бесконечности.
7. Какой вид имеет частотный спектр единичной ступенчатой функции и единичной импульсной функции.
Преобразование F (j w, c) носит название обобщенного преобразования Фурье. Для получения спектра единичной функции перейдем к пределу:
Единичная импульсная функция:
Таким образом, d-функция имеет равномерный амплитудный и нулевой фазовый спектры. Равенство нулю на всех частотах фазового спектра означает, что все гармонические составляющие d-функции, суммируясь с нулевыми начальными фазами, образуют при t = 0 пик бесконечно большого значения.
8. Как определяется ширина сплошного частотного спектра и ширина дискретного частотного спектра.
Ширина спектра апериодического сигнала определяется, как часть спектра, в которой сосредоточена заданная доля (90 или 95%) энергии сигнала.
Решение этой задачи основано на теореме Релея – равенстве Парсеваля интеграла Фурье. В соответствии с этой теоремой распределение энергии риодического сигнала по частоте можно определить из выражения:
Ширина спектра сигнала (F) это диапазон частот, в пределах которого сосредоточена его основная энергия. Она определяет скорость изменения сигнала внутри интервала его существования
Как видно из диаграмм спектр ПППИ является дискретным и неограниченным. Поэтому за ширину спектра принимают диапазон частот, в пределах которого находится два первых лепестка, т. к. в них содержится около 95% энергии сигнала:
9. Как связана ширина частотного спектра сигнала с длительностью (шириной) сигнала.
База сигнала есть произведение длительности сигнала на ширину его спектра 
. Необходимо отметить, что между шириной спектра и длительностью сигнала существует обратно пропорциональная зависимость: чем короче спектр, тем больше длительность сигнала. Таким образом, величина базы остается практически неизменной;
10. Порядок формирования уравнений цепи с применением метода узловых напряжений.
Для выходных узлов уравнение не может быть составлено,так как при нулевых выходных сопротивлениях идеальных усилителей их выходные проводимости равны бесконечтности.
В узловых цепях, содержащих идеальные усилители,узловое уравнение для выходного узла не составляют. Вместо этого рекомендуется использовать уравнение U2(p)=k*U4(p)
Формирование уравнений электрической цепи с идеальными усилителями имеет следующие особенности:
- при формировании уравнения для входного узла влияние усилителя не
учитывается, так как ток во входной ветви идеального усилителя равен нулю;
- для выходного узла узловое уравнение не может быть составлено, так
как при нулевом выходном сопротивлении идеального усилителя его выходная
проводимость равна бесконечности;
- систему узловых уравнений необходимо дополнить уравнением связи
входного и выходного напряжений усилителя, в результате получим систему,
в которой число уравнений равно числу неизвестных.
Напряжение на входе и выходе усилителя с конечным коэффициентом
усиления связаны уравнением:U10(p)=k*U20(p)
где U10(p) - операторное напряжение на входе; U20(p) - операторное напряжение на выходе; k - коэффициент усиления.
Алгоритм формирования узловых уравнений включает следующие шаги.
1. Выбираем базисный узел.
2. Остальным узлам присваиваем номера 1,, 2, 1 -
3. Представляем матрицу узловых проводимостей в виде таблицы,
4. Полагаем все элементы матрицы узловых проводимостей и векторы
узловых токов равными нулю. Это эквивалентно исключению из схемы всех
элементов.
5. Поочередно включаем элементы в схему. Если резистор включен
между узлами i и j, его проводимость записываем в элементы матрицы,
расположенные на пересечении строк и столбцов с номерами i и j (рис. 3.2).
Если резистор включен между узлом i и базисным, его проводимость запи-
сываем в собственную проводимость i-го узла ii
g. Если между узлами i и j
включен источник тока, его ток записываем в i-ю и j-ю строки вектора узло-
вых токов.
6. Формирование узловых уравнений заканчивается, когда в схему
включены все элементы.
11. Запишите выражение для прямого и обратного преобразования Лапласа и объясните их
Структуру.
Прямое преобразование Лапсаса заключается в переводе некоторой функции времени f(t) в операторную форму F(p). Это преобразование означает вычисление интеграла
Прямым преобразованием Лапласа функции действительного переменного 
называется функция комплексного переменного 
определяемая формулой
. (1)
В случае, если функция существует, то функция действительного переменного 
называется оригиналом, а функция комплексного переменного - ее изображением.
Если функция является оригиналом, а - ее изображением, то в любой точке 
, где оригинал непрерывен, имеет место формула
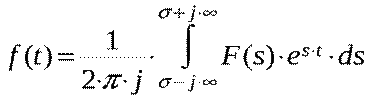, (2)
При использовании операторного метода устанавливается соответствие между функцией f(t) – оригиналом и операторным изображением этой функции – F(p).
Данное соответсвие устанавливается на основании прямого интегрального преобразования Лапласа: 
f(t) – оригинал функции,
F(p) – Изображения этой функции по Лапласу
p – оператор Лапласа, p = Ƈ+jw
12. Какие свойства приписывают идеальному операционному усилителю.
Идеальный ОУ описывается формулой (1) и обладает следующими характеристиками:
1. Бесконечно большой коэффициент усиления с разомкнутой петлей обратной связи G openloop.[3]
2. Бесконечно большое входное сопротивление входов V - и V +. Другими словами, ток, протекающий через эти входы, равен нулю.
3. Нулевое выходное сопротивление выхода ОУ.
4. Способность выставить на выходе любое значение напряжения.
5. Бесконечно большая скорость нарастания напряжения на выходе ОУ.
6. Полоса пропускания: от постоянного тока до бесконечности.
· бесконечно большой дифференциальный коэффициент усиления по напряжению KU=Uвых /(U1 - U2) (у реальных ОУ от 1 тыс. до 100 млн.);
· нулевое напряжение смещения нуля Uсм, т.е. при равенстве входных напряжений выходное напряжение равно нулю (у реальных ОУ Uсм, приведенное ко входу, находится в пределах от 5 мкВ до 50 мВ);
· нулевые входные токи (у реальных ОУ от сотых долей пА до единиц мкА);
· нулевое выходное сопротивление (у реальных маломощных ОУ от десятков Ом до единиц кОм);
· коэффициент усиления синфазного сигнала равен нулю;
· мгновенный отклик на изменение входных сигналов (у реальных ОУ время установления выходного напряжения от единиц наносекунд до сотен микросекунд).
13. Дайте определение операторной передаточной функции и назовите ее основные свойства.
Важную роль в методах анализа и синтеза электрических цепей при нулевых начальных условиях играют операторные передаточные функции, которые определяются как отношение изображения выходной реакции цепи к изображению входного воздействия. В соответствии с этим определением различают четыре вида передаточных функций:
где Ни (р), Hi (p) имеют смысл операторных передаточныхфункций по напряжению и току; НL (р); НY (р) —операторные передаточные сопротивление и проводимость соответственно.
Перечислим основные свойства операторных передаточных функций:
· Операторная передаточная функция является обобщенным описанием связей сигналов на входе и выходе и определяет характер преобразования сигнала, который зависит от параметров и способов соединения элементов.
· Знаменатель передаточной функции является характеристическим полиномом,а его корни – корнями характеристического уравнения.
1. Передаточная функция является дробно-рациональной функцией с вещественными коэффициентами. Вещественность коэффициентов объясняется тем, что они определяются элементами схемы.
2. Знаменатель и числитель передаточной функции — это характеристические полиномы системы. Полюсы передаточной функции — это корни характеристического полинома в знаменателе, нули — корни характеристического полинома в числителе.
3. Полюсы передаточной функции располагаются в левой полуплоскости комплексной переменной р. На расположение нулей ограничений нет. Докажем это свойство на примере передаточной функции Ни (р) = U 2(р)/ U 1(р). Выберем входное воздействие u 1(t) = d(t) или в операторной форме U (р) = l. Изображение выходного напряжения U 2(р) = U 1(р) Ни (р) в этом случае численно равно Ни (р), т. е.
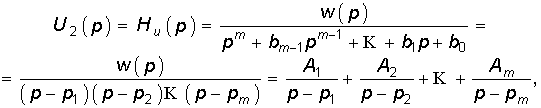
где w (p) — полином числителя передаточной функции; A 1, A 2,..., Am, — коэффициенты разложения дробно-рациональной функциина сумму простых дробей.
Перейдем от изображения U 2(p) к оригиналу u 2(t):
где в общем случае pi = a i + j w i.
В пассивных и устойчивых активных четырехполюсниках колебания на выходе четырехполюсника после прекращения воздействия должны иметь затухающий характер. Это означает, что в (7.46) вещественные части полюсов pi должны быть отрицательными (a i < 0), т. е. полюсы должны находиться в левой полуплоскости переменной р.
3. Степени полиномов числителей передаточной функции не превышают степеней полиномов знаменателей, т. е. п < т. Если бы это свойство не выполнялось, то на бесконечно больших частотах АЧХ принимала бы бесконечно большое значение (так как числитель рос бы с увеличением частоты быстрее знаменателя), т. е. цепь обладала бы бесконечным усилением, что противоречит физическому смыслу.
14. Что называется электрическим фильтром. Назовите условия передачи сигнала через фильтр без искажения.
Устройство, пропускающее определенную часть спектра сигнала, называется фильтром. Одно из применений фильтра – борьба с помехами, основной источник которых – электромагнитные поля с частотой 50 Гц. В аппаратуре ставятся полосовые фильтры, не пропускающее сигнал с частотой 50 Гц, или фильтры, ограничивающие полосу пропускания сигнала от самых низких частот до 50 Гц.
Электрическим фильтром называется четырехполюсник, предназначенный для передачи
без искажений части спектра сигнала,лежащего в определенном диапазоне частот –
полосе пропускания, и подавления спектральных составляющих сигналов, лежащих
в полосе непропускания фильтра.
Для передачи сигнала без искажения необходимо равенство единице амплитудно-частотной характеристики фильтра в полосе пропускания и линейная зависимость от частоты фазового сдвига q. Однако, как будет показано ниже, их строгое выполнение на практике невозможно.
Что необходимо для того, чтобы сеть вела себя как идеальный канал передачи? Сигнал на выходе идеального канала связи может запаздывать по отношению к сигналу на входе; кроме того, эти сигналы могут иметь различные амплитуды (простое изменение масштаба), но что касается всего остального - сигнал не должен быть искажен, т.е. он должен иметь ту же форму, что и сигнал на входе. Следовательно, для идеальной неискаженной передачи выходной сигнал мы можем описать как
, (1.54)
где 
и 
- константы. Применив к обеим частям преобразование Фурье (см. раздел А.3.1), имеем следующее.
(1.55)
Подставляя выражение (1.55) в уравнение (1.49), видим, что необходимая передаточная функция системы для передачи без искажений имеет следующий вид.
(1.56)
Следовательно, для получения идеальной передачи без искажений общий отклик системы должен иметь постоянный модуль, а сдвиг фаз должен быть линейным по частоте. Недостаточно, чтобы система равно усиливала или ослабляла все частотные компоненты. Все гармоники сигнала должны поступать на выход с одинаковым запаздыванием, чтобы их можно было просуммировать. Поскольку запаздывание связано со сдвигом фаз 
и циклической частотой 
соотношением
, (1.57,а)
очевидно, что, для того чтобы запаздывание всех компонентов было одинаковым, сдвиг фаз должен быть пропорционален частоте. Для измерения искажения сигнала, вызванного запаздыванием, часто используется характеристика, называемая групповой задержкой; она определяется следующим образом.
(1.57,б)
Таким образом, для передачи без искажений имеем два эквивалентных требования: фаза должна быть линейной по частоте или групповая задержка 
должна быть равна константе. На практике сигнал будет искажаться при проходе через некоторые части системы. Для устранения этого искажения в систему могут вводиться схемы коррекции фазы или амплитуды (выравнивания). Вообще, искажение - это общая характеристика ввода-вывода системы, определяющая ее производительность.
15. Назовите основные типы электрических фильтров и объясните их частотные характеристики (АЧХ).
По расположению полосы пропускания на шкале частот различают сле-
дующие фильтры:
- нижних частот (ФНЧ), в которых полоса пропускания располагается на
шкале частот от ω = 0 до некоторой граничной частоты ω = ω п, а полоса не-
пропускания (задерживания) – от частоты ω = ω з до бесконечно больших час-
(рис. 1.1, а);
- верхних частот (ФВЧ) с полосой пропускания от частоты ω = ω п до
бесконечно больших частот и полосой непропускания от частоты ω= 0 до
ω з (рис. 1.1, б);
- полосовые (ПФ), в которых полоса пропускания ω п1 …ω п2 располагается
между полосами непропускания 0…ω з1 и ω з2 …8 (рис. 1.1, в);
- заграждающие (режекторные) (ЗФ или РФ), в которых между полосами
пропускания 0…ω п1 и ω п2 …8 находится полоса непропускания ω з1 …ω з2 (рис.
г);
- многополосные, имеющие несколько полос пропускания.
На рис. 1.1, а—г показаны также условные обозначения фильтров каждого
типа в соответствии с ГОСТ. Диапазон частот, разделяющий полосы пропус-
кания и непропускания, называется полосой перехода.
Рис. 1.1
Фильтр верхних частот (ФВЧ) — электронный или любой другой фильтр, пропускающий высокие частоты входного сигнала, при этом подавляя частоты сигнала ниже частоты среза. Степень подавления зависит от конкретного типа фильтра.
Термины «высокие частоты» и «низкие частоты» в применении к фильтрам относительны и зависят от выбранной структуры и параметров фильтра.
Фильтр ни́жних часто́т (ФНЧ) — один из видов аналоговых или электронных фильтров, эффективно пропускающий частотный спектр сигнала ниже некоторой частоты (частоты среза), и уменьшающий (подавляющий) частоты сигнала выше этой частоты. Степень подавления каждой частоты зависит от вида фильтра.
Полосно-пропускающий фильтр — фильтр, который пропускает частоты, находящиеся в некоторой полосе частот.
Полосно-заграждающий фильтр (проф. жаргон — режекторный фильтр, фильтр-пробка) — электронный или любой другой фильтр, не пропускающий колебания некоторой определённой полосы частот, и пропускающий колебания с частотами, выходящими за пределы этой полосы.
16. Дайте определение активного RC фильтра. Назовите характерные особенности фильтра.
Активные фильтры включают пассивные элементы R,C и усилители напряжения (операционные усилители).
Активный фильтр — один из видов аналоговых электронных фильтров, в котором присутствует один или несколько активных компонентов, к примеру транзистор или операционный усилитель.
В активных фильтрах используется принцип отделения элементов фильтра от остальных электронных компонент схемы. Часто бывает необходимо, чтобы они не оказывали влияния на работу фильтра. Применение усилителей в активных фильтрах позволяет увеличить наклон частотной характеристики в полосе подавления, что недостижимо при каскадном соединении пассивных RC-цепочек.
К недостаткам активных фильтров можно отнести следующее:
• активные фильтры не могут работать на таких высоких частотах, на ко-
торых операционные усилители уже не способны усиливать сигнал,
• активные фильтры нуждаются в источниках питания,
• возможна потеря устойчивости режима работы, что может привести к
неограниченному росту токов и напряжений при ограниченном входном воз-
действии.
В активных фильтрах, или фильтрах с обратными связями, используется
параллельное соединение и другие виды соединений четырехполюсников. Че-
тырехполюсник, по которому сигнал проходит с входа на выход, является не-
селективной цепью с коэффициентом передачи, не зависящим от частоты. В
качестве такого четырехполюсника часто используют операционный усили-
тель. Четырехполюсник обратной связи обычно содержит селективную цепь.
17. Что называется переходной характеристикой электрической цепи. Назовите методы ее расчета.
Переходной характеристикой h(t) называется реакция электрической цепи при нулевых начальных условиях на единичную ступенчатую функцию l(t). Импульсной характеристикой g(t) называется реакция цепи на воздействие в виде единичной импульсной функции d (t). Обе характеристики определяются при нулевых начальных условиях.
Переходная и импульсная функции характеризуют цепь в переходном режиме, так как они являются реакциями на скачкообразные, т.е. довольно тяжелые для любой системы воздействия. Кроме того, как будет показано ниже с помощью переходной и импульсной характеристик может быть определена реакция цепи на произвольное воздействие.
Переходная и импульсная характеристики связаны между собой также как связаны между собой соответствующие воздействия. Единичная импульсная функция является производной от единичной ступенчатой функции,поэтому импульсная характеристика является производной от переходной характеристики и при h (0)= 0
Чтобы определить переходную характеристику H(p)/p, invlap
18. Какая система называется устойчивой. К чему ведет потеря устойчивости электрической цепи.
Цепь называется устойчивой, если свободные колебания с течением времени стремятся к нулю. В противном случае цепь называется неустойчивой. Из теории переходных процессов следует, что цепь является устойчивой, если корни характеристического уравнения лежат в левой полуплоскости комплексной переменной р. Есликорни такого уравнения лежат в правой полуплоскости, то цепь является неустойчивой, т. е. она находится в режиме самовозбуждения.
Неустойчивость может наблюдаться в активных электрических цепях с обратными связями. В этих цепях энергия, накапливаемая пассивными элементами при переходном процессе, восполняется управляемыми источниками, что может привести к неограниченному росту напряжений и токов при ограниченном внешнем воздействии
Поэтому в устойчивой цепи, в которой свободная составляющая f" стремится с течением времени к нулю, все вещественные корни характеристического уравнения должны быть отрицательными,а комплексные -иметь отрицательную вещественную часть Это же относится к кратным корням.
Анализ устойчивости производится по расположению корней характеристического полинома передаточной функции исследуемой цепи на комплексной плоскости. При этом можно непосредственно находить значения корней (полюсов передаточной функции) или воспользоваться для этой цели критериями устойчивости. Для определения полюсов передаточной функции характеристический полином каждого звена электрического фильтра следует приравнять к нулю и найти их корни. Такой подход рекомендуется применять для полиномов порядка не более третьего.
19. Что значит работа электрической цепи на границе устойчивости. Дайте определение понятию «автоколебательный режим».
Цепи без потерь (включающие только L и С) находятся на границе устойчивости (точки на оси Y), поскольку их характеристические уравнения имеют чисто мнимые корни, отвечающие собственным частотам цепи ω0. Такому положению корней соответствует незатухающий переходный процесс
Автоколебательный режим, при котором генерация импульсов происходит непрерывно пока включены источники питания.
В некоторых «саморегулирующихся» системах незатухающие колебания могут поддерживаться постоянной внешней силой. Такие системы называются автоколебательными, а их поведение называется автоколебаниями
20. Дайте определение понятию «критерии устойчивости». Назовите признаки, по которым определяется устойчивость по критерию Гурвица.
Критерий формулируется следующим образом: цепь с обратной связью является устойчивой, если полином характеристического уравнения, является полиномом Гурвица. При этом используется основное свойство полинома Гурвица: все его корни находятся в левой полуплоскости комплексной переменной р.
21. Дайте понятие обратной связи. Запишите выражение передаточной функции четырехполюсника с обратной связью.
При каскадном соединении, когда сигнал последовательно проходит несколько четырехполюсников, их передаточные функции перемножаются:
.
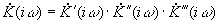Это непосредственно следует при замене коэффициентов передачи отношением комплексных амплитуд выходных и входных напряжений каждого четырехполюсника.
Обратная связь в четырехполюсниках заключается в том, что часть выходного сигнала подается обратно на вход и суммируется с входным сигналом.
| Пусть K(iw) – передаточная функция основного четырехполюсника,  - передаточная функция четырехполюсника обратной связи.
|
; 
.
Отсюда 
.
Итак, общий коэффициент передачи системы с обратной связью есть
.
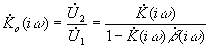22. Какую функцию называют передаточной функцией по петле обратной связи. Запишите выражение и сформулируйте критерий устойчивости Найквиста.
Передаточная функция по петле обратной связи – отношение напряжений U1 к U2, где U1 – напряжение перед разрывом цепи обратной связи на входе усилителя, а U2 – после.
B(jw)=U1(jw)/U2(jw)
Если годограф данной функции не охватывает точку (1; j0), то по критерию Найквиста данная цепь устойчива.
23. В чем суть критерия устойчивости Михайлова. Объясните на анализе каких свойств цепей и описывающих их функций основан этот критерий.
Критерий устойчивости Найквиста. Он относится к частотным крите-
риям и основан на анализе частотных свойств цепи по петле обратной связи.
Его можно сформулировать в геометрической трактовке так: система с об-