1. Распределение торговых фирм по размеру месячного товарооборота характеризуется следующими данными:
| Товарооборот, млрд.руб. | До 5 | 5-10 | 10-15 | 15-20 | 20-25 | 25 и более | Итого |
| Число фирм |
Определите:
а) модальное и медианное значение месячного товарооборота;
б) средний размер товарооборота на одну фирму.
2. По данным Госкомстата РФ численность занятых в экономике по возрасту в 2010 г. распределялась так:
| Возраст, лет | До 19 | 20-24 | 25-29 | 30-34 | 35-39 | 40-44 | 45-49 | 50-54 | 55-59 | 60-72 | Итого |
| % к общей численности занятых | 1,5 | 9,2 | 11,5 | 11,6 | 15,3 | 17,0 | 15,4 | 10,7 | 3,6 | 4,2 |
Определите медиану, первый и третий квартили, первый и девятый децили.
Ответ: Ме = 
= 40,2;
Q1 = 
= 31,0; Q3 =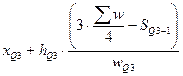 
= 47,3;
D1 = 
= 23,7; D9=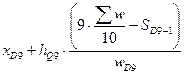 
= 53,2
3. Определите среднее линейное отклонение, дисперсию, СКО, относительные показатели вариации для распределения 20 банков по величине прибыли.
| Прибыль, млн.руб. | Число банков |
| 3,7-4,5 | |
| 4,5-5,3 | |
| 5,3-6,1 | |
| 6,1-6,9 | |
| 6,9-7,7 | |
| Итого |
4. Имеются следующий данные о балансовой прибыли предприятий за два квартала:
| Квартал | Число предприятий | Балансовая прибыль, млрд.руб. |
| I | 18,4; 38,8; 72,6 | |
| II | 14,1; 16,3; 48,8; 27,9 |
Определите:
а) среднюю из внутригрупповых, межгрупповую и общую дисперсию балансовой прибыли;
б) показатели тесноты связи между кварталом и балансовой прибылью предприятий (коэффициент детерминации и эмпирическое корреляционное отношение).
Или другими словами: Используя метод дисперсионного анализа (правило сложения дисперсий), установить существует ли зависимость между кварталом и балансовой прибылью.
5. Имеются данные по молочно – товарным фермам хозяйства об общем поголовье коров и числе дойных коров.
| Ферма | Всего коров, голов | В том числе дойных |
Определите:
а) дисперсию доли дойных коров по отдельным молочно-товарным фермам;
б) среднюю их внутригрупповых дисперсий;
в) межгрупповую дисперсию;
г) общую дисперсию доли дойных коров по фермерскому хозяйству в целом.
6. Распределение рабочих двух участков по стажу работы следующие:
| Стаж работы, лет | Число рабочих, чел. | |
| Участок №1 | Участок №2 | |
| 0-5 5-10 10-15 15-20 |
Определите, на каком участке состав рабочих по стажу работы более однороден.
Ответ: Vσ_1 = 39,90% Vσ_2 = 48,62% → более однороден состав рабочих по стажу работы на 1 участке.
7. По группе промышленных предприятий имеются следующие данные:
| Группы предприятий по стоимости основного капитала, млн.руб. | Число предприятий | Средний объем продукции в группе, млн.руб. | Внутригрупповая дисперсия объема продукции |
| 40-50 50-60 60-70 | 90,7 115,8 84,0 |
Определите коэффициент детерминации и эмпирическое корреляционное отношение.
Ответ: 
= 0,9828 → 
= 0,9914 или 99,14 %
8. Рассчитайте показатели ассиметрии и эксцесса по данным задачи 3.
| Прибыль, млн.руб. | Число банков |
| 3,7-4,5 | |
| 4,6-5,4 | |
| 5,5-6,3 | |
| 6,4-7,2 | |
| 7,3-8,1 | |
| Итого |
9. Постройте теоретическую кривую нормального распределения по данным задачи 3. Определите критерий согласия Пирсона (χ2) и проверьте близость эмпирического и теоретического распределений прибыли 20 коммерческих банков.
Или другими словами: Исходя из гипотезы о нормальном распределении, рассчитать теоретические частоты. Проверить соответствие эмпирических и теоретических частот с помощью критерия Пирсона.
10. По данным задачи 1 постройте теоретическую кривую нормального распределения и проверьте близость эмпирического и теоретического распределений с помощью критериев Романовского и Колмогорова.
Решение:
| х | f | х*f | (х-  )2*f
| t | φ(t) | ft | (f-ft)2/ft | S | St | 
|
| 2,5 | 702,25 | -2,08 | 0,05 | 0,42 | ||||||
| 7,5 | 816,75 | -1,29 | 0,17 | 0,12 | ||||||
| 12,5 | 190,125 | -0,51 | 0,35 | 0,72 | ||||||
| 17,5 | 79,625 | 0,27 | 0,38 | 0,15 | ||||||
| 22,5 | 637,875 | 1,06 | 0,23 | 0,01 | ||||||
| 27,5 | 828,375 | 1,84 | 0,07 | 0,44 | ||||||
| Итого | 1,86 |
= 1260/80 = 15,75; σ =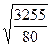 
= 6,38; h = 5
= 1,86; к = 6-3 = 3
Расхождение = 
= 0,31 < 2, значит расхождение не большое
Критерий согласия Романовского R0 = 
= 0,47
D = max = 2 → Критерий согласия Колмогорова λ= 
= 0,22
11. Средняя величина в совокупности равна 15, среднее квадратическое отклонение равно 10. Чему равен средний квадрат индивидуальных значений этого признака?
12. Средняя величина признака в совокупности равна 13, а средний квадрат индивидуальных значений этого признака равен 174. Определите коэффициент вариации.
13. Дисперсия признака равна 360000, коэффициент вариации равен 50%. Чему равна средняя величина признака?
Ответ: = 1200
14. Дисперсия признака равна 25, средний квадрат индивидуальных значений равен 250. Чему равна средняя?
Ответ: = 15
15. Определите дисперсию признака, если средняя величина признака равна 2600, а коэффициент вариации равен 30%.
Ответ: σ2 = 608400
16. Общая дисперсия равна 8,4. Средние по группам равны соответственно 10,15 и 12. Численность единиц в каждой группе составляет 32,53 и 45. Определите межгрупповую и среднюю из внутригрупповых дисперсий.
Ответ: δ2 = 4,12;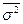 
= 4,28