Перевод чисел из любой системы счисления в десятичную.

Практическая работа № 5.

Представление информации в различных системах счисления.

Цель: научиться переводить числа из одной системы счисления в другую.

Краткие теоретические сведения.

Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.

Непозиционной называется такая система счисления, в которой количественный эквивалент каждой цифры не зависит от ее положения (места, позиции) в записи числа.

Основанием системы счисления называется количество знаков или символов, используемых для изображения числа в данной системе счисления.

Наименование системы счисления соответствует ее основанию (например, десятичной называется система счисления так потому, что ее основание равно 10, т.е. используется десять цифр).

Система счисления называется позиционной, если значение цифры зависит от ее места (позиции) в записи числа.

Системы счисления, используемые в компьютерах

Двоичная система счисления. Для записи чисел используются только две цифры – 0 и 1. Выбор двоичной системы объясняется тем, что электронные элементы, из которых строятся ЭВМ, могут находиться только в двух хорошо различимых состояниях. По существу, эти элементы представляют собой выключатели. Как известно выключатель либо включен, либо выключен. Третьего не дано. Одно из состояний обозначается цифрой 1, другое – 0. Благодаря таким особенностям двоичная система стала стандартом при построении ЭВМ.

Восьмеричная система счисления. Для записи чисел используется восемь чисел 0,1,2,3,4,5,6,7.

Шестнадцатеричная система счисления. Для записи чисел в шестнадцатеричной системе необходимо располагать шестнадцатью символами, используемыми как цифры. В качестве первых десяти используются те же, что и в десятичной системе. Для обозначения остальных шести цифр (в десятичной они соответствуют числам 10,11,12,13,14,15) используются буквы латинского алфавита – A, B, C, D, E, F.

Перевод чисел из одной системы счисления в другую.

Правило перевода целых чисел из десятичной системы счисления в систему с основанием q:

1. Последовательно выполнять деление исходного числа и получаемых частных на q до тех пор, пока не получим частное, меньшее делителя.

2. Полученные при таком делении остатки – цифры числа в системе счисления q – записать в обратном порядке (снизу-вверх).

Примеры решения заданий.

Пример 1. Перевести 26₁₀ в двоичную систему счисления. А₁₀→А₂

Решение:

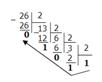
Ответ: 26₁₀=11010₂

Пример 2. Перевести 19₁₀ в троичную систему счисления. А₁₀→А₃.

Решение:

Ответ: 19₁₀=201₃.

Пример 3. Перевести 241₁₀ в восьмеричную систему счисления. А₁₀→А₈

Решение:

Ответ: 241₁₀=361₈.

Пример 4. Перевести 3627₁₀ в шестнадцатеричную систему счисления. А₁₀→А₁₆

Решение:

Т.к. в шестнадцатеричной системе счисления 14 – Е, а 11 – В, то получаем ответ Е2В₁₆.

Ответ: 3627₁₀=E2B₁₆.

Перевод чисел из любой системы счисления в десятичную.

Правило: Для того чтобы число из любой системы счисления перевести в десятичную систему счисления, необходимо его представить в развернутом виде и произвести вычисления.

Пример 5. Перевести число 110110₂ из двоичной системы счисления в десятичную.

Решение:

110110₂ = 1*2⁵ + 1*2⁴ + 0*2³+1*2²+1*2¹+0*2⁰=32+16+4+2=54₁₀.

Ответ: 110110₂ = 54₁₀.

Пример 6. Перевести число 101,01₂ из двоичной системы счисления в десятичную.

Решение:

101,01₂ = 1*2² + 0*2¹ + 1*2⁰+0*2-¹+1*2^-2 =4+0+1+0+0,25=5,25₁₀.

Ответ: 101,01₂ = 5,25₁₀.

Пример 7. Перевести число 122100₃ из троичной системы счисления в десятичную.

Решение:

12201₃=1*3⁴ + 2*3³ + 2*3² + 0*3¹ + 1*3⁰ = 81+54+18+1 = 154₁₀.

Ответ: 12201₃ = 154₁₀.

Пример 8. Перевести число 163₇ из семеричной системы счисления в десятичную.

Решение: 163₇ = 1*7² + 6*7¹ + 3*7⁰ = 49+42+3= 94₁₀.

Ответ: 1637 = 94.

Пример 9. Перевести число 2Е₁₆ в десятичную систему счисления.

Решение:

2Е₁₆ = 2*16¹ +14*16⁰ = 32 +14 = 46₁₀.

Ответ: 2Е₁₆ = 46₁₀.