Трехкомпонентные системы.
Изображение состава СИСТЕМЫ.
Растворы, содержащие три компонента, удобнее рассматривать, пользуясь диаграммой, отображающей содержание каждого из компонентов системы. Для этого могут быть использованы различные формы графиков.
Часто пользуются равносторонним треугольником – треугольником Гиббса:
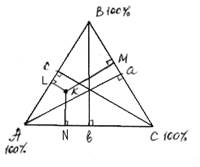
В каждой вершине треугольника располагается чистое вещество: точка А – чистое вещество А (100 %). Каждая сторона треугольника характеризует двухкомпонентный состав, например, сторона АС характеризует состав раствора АС. Из каждой вершины треугольника опущен перпендикуляр: Аа, Вв, Сс. Перпендикуляры обычно разбивают на 100 или 10 частей, тогда точка А – 100 % вещества А, точка а – 0 % вещества А.
Рассмотрим фигуративную точку К, лежащую внутри области треугольника. Из этой точки на каждую сторону треугольника опускаем перпендикуляр.
Содержание вещества А пропорционально длине отрезка КМ, т.е. отрезка, находящегося на противоположной стороне треугольника от данной вершины.
Вещество А → KM
Вещество В → KN
Вещество С → KL
Сумма длин этих отрезков равна длине перпендикуляра, например: Аа=100%= KM+KN+КL.
Треугольник Розебума:
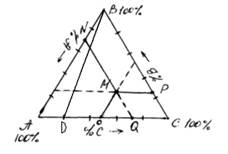
Каждую сторону треугольника делят на 100 или 10 равных частей, получая процентное содержание компонентов двухкомпонентной смеси.
Рассмотрим фигуративную точку М. Проведем через точку М прямые, параллельные сторонам треугольника. Процентное содержание компонента А определяется отрезком МР (точка Р лежит на стороне ВС).
Вещество А → MР
Вещество В → MО
Вещество С → MN
Треугольные диаграммы Розебума основаны на следующем свойстве: сумма отрезков прямых, проведенных параллельно сторонам равностороннего треугольника через любую точку, лежащую внутри этого треугольника, есть величина постоянная, равная стороне треугольника: MР + MО + MN=АВ=ВС=АС=100%.
Метод Розебума получил более широкое применение, так как он позволяет судить о содержании в системе всех трех компонентов по делениям, нанесенным на одной стороне треугольника.
Так, принимая сторону АС за 100 % и учитывая, что MP=QC, MО=ОQ, MN=АО, получим состав, изображенный фигуративной точкой М:
Вещество А =QC
Вещество В =QО
Вещество С =АО
Точки, лежащие на прямой BD, проходящей через вершину треугольника (В), изображают составы системы с постоянным соотношением концентраций двух других компонентов А и С; А:С=80:20=4:1.
Ограниченная растворимость в тройных жидких системах.
Рассмотрим систему, состоящую из двух нерастворимых жидкостей (вода+хлороформ). Добавляем туда третье вещество (ацетон), способный растворяться как в воде, так и в хлороформе.
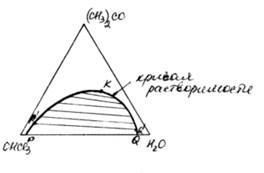
Вершины треугольника соответствуют чистым компонентам. Поскольку каждая сторона треугольника соответствует двойной системе, то из диаграммы видно, что хлороформ и ацетон и вода и ацетон хорошо смешиваются, т.е. полностью растворимы, а хлороформ и вода имеют ограниченную растворимость. Двойная система хлороформ–вода при любых соотношениях, ограниченных кривой растворимости, будет образовывать два жидких слоя, т.е. расслаиваться. РКQ – гетерогенная система, выше РКQ – гомогенная система. Точки на кривой растворимости изображают состав расслаивающейся жидкости. Линия, соединяющая эти точки, например, Р΄Q΄, называется линией сопряжения, или нодой. В отличие от диаграмм растворимости для двойных систем, где линии сопряжения параллельны друг другу, на тройной диаграмме эти линии, как правило, не горизонтальны. Наклон их зависит от того, насколько неодинаково растворяется в двух жидких фазах третье вещество. Т.е. концентрация ацетона в слое хлороформа при равновесии выше, чем в слое воды, поэтому линии располагаются наклонно.
При добавлении третьего вещества растворимость двух ограниченно растворимых жидкостей может заметно изменяться. При добавлении ацетона к двухслойной системе из хлороформа и воды увеличивается их взаимная растворимость вплоть до образования однородной (гомогенной) смеси. При этом составы равновесных слоев сближаются и точка К отвечает достижению ими одинакового состава, т.е. образованию гомогенной системы. Точку К обычно называют критической точкой.