Большинство реальных жидких растворов не обладают свойствами идеальных. У неидеальных растворов концентрация перестает адекватно отражать состояние системы. Поэтому для характеристики свойств реальных растворов используют активность.
Активность, или термодинамическая активность, является условной эффективной концентрацией, которая позволяет уравнения, характеризующие термодинамические свойства идеальных растворов, использовать для реальных растворов.
Активность выражается:
; 
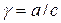, где
а – активность; с – молярная концентрация; γ – безразмерный коэффициент активности.
Активность можно выразить через различные концентрации:
m – моляльная концентрация;
N – мольная доля.
Для разбавленных растворов коэффициенты активности 
примерно равны.
Коэффициент активности характеризует степень отклонения свойств реальных растворов от идеальных. Для идеальных растворов 
.
Коллигативные свойства раствора выражают через изменение химического потенциала. С учетом формулы 
:
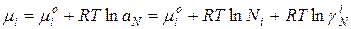
Для идеального раствора:
Поэтому химический потенциал реального раствора отличается от химического потенциала идеального раствора на величину 
или 
.
Коэффициент активности соответствует дополнительной работе, которую необходимо затратить при P, T = const для преодоления взаимодействия между частицами раствора при переносе одного моля компонента идеального раствора в реальный раствор той же концентрации. Менее концентрированному раствору отвечает и меньшая работа переноса. Для идеального раствора эта работа обращается в ноль.
Итак, активность, как аналог концентрации, следует подставить в выражение для химического потенциала компонента идеального раствора, чтобы получить выражение для химического потенциала реального раствора.
|
|
Для определения стандартного химического потенциала µ0 неидеальных растворов важное значение приобретает выбор стандартного состояния. Обычно принимают стандартное состояние при определенных P и T = const, и когда а =1 и N=1. Тогда 
– для растворителя.
За стандартное состояние растворенного вещества принимают такое, при котором его активность равна концентрации, т.е. 
.
Тогда 
.
Это уравнение фиксирует тот факт, что раствор ведет себя как идеальный:
Знак разности 
определяет характер отклонений реального раствора от идеального. При 
эти отклонения отрицательные: химический потенциал идеального раствора превышает химический потенциал реального 
. Если 
, а 
, то эти отклонения положительные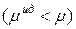 
; они наблюдаются чаще.
Понятия об активности и о коэффициенте активности являются одними из фундаментальных и основных в физической химии. Активность выражает все термодинамические свойства растворов: для идеальных растворов она совпадает с концентрацией, а для реальных растворов показывает степень их отклонения от идеальных. Коэффициент активности устанавливает непосредственную связь активности с концентрацией. Коэффициент активности может быть больше и меньше единицы, а следовательно, активность может быть больше или меньше концентрации.
Рассмотрим 2 метода определения активности и коэф-та активности.
1 метод:
Выразили химический потенциал при помощи формулы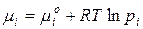 
и заменили это уравнение для реального раствора в любом состоянии и в стандартном состоянии (
для растворителя:
|
|
; (1)
; (2)
где 
– парциальное давление паров над раствором;
– парциальное давление паров над растворителем.
Вычтем из (1) (2) уравнение и с учетом условия р 
, получим
, т.е. 
=p 
/p 
Таким образом, активность компонента в растворе равна отношению парциального давления пара над раствором к давлению паров растворителя.
Пример. Водный раствор содержит m 
, m 
Давление паров этилового спирта и воды при 20 
C в этом растворе равны p 
мм.рт.ст. (1,68 
Па) и р 
мм.рт.ст.(2,12 Па). Давление паров чистых веществ р 
мм.рт.ст. (2,33 Па) и спирта р 
=43,6 мм.рт.ст. (5,81 
Па).
Рассчитать 
-? и 
-?, а также 
—?
Активность воды 
Активность спирта 
г/моль; 
г/моль;
Число моль воды: n 
моль;
Число моль спирта: n 
моль;
Мольная доля воды: N 
Мольная доля спирта: 
Коэффициент активности воды и спирта: 
Химический потенциал воды в растворе:
(по таблицам 
кДж/моль).
2 метод:
Основан на определении понижения температуры замерзания раствора.
Из формулы 
Опытным путем определяем коэффициент j, который характеризует, насколько повышается температура замерзания раствора:
j=1- 
Для разбавленных растворов можно использовать приближенную формулу для расчета коэффициента активности:
ln 
Пример. Рассчитаем активность и коэффициент активности 3,5 – моляльного раствора глицерина в воде, если его температура замерзания – 7,5 С, а криоскопическая постоянная воды равна K=1,86 K∙кг/моль
m=3,5 моль/1 кг 
; T 
;K=1,86 K 
Рассчитаем коэффициент:
j=1- 
.
Коэффициент активности:
ln 
Активность находим по формуле:
|
|
моль/кг
По аналогии с коэффициентом активности для расчета осмотического давления реальных растворов используют осмотический коэффициент:
= 
; 
где 
, 
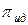-осмотическое давление реального и идеального растворов.
Осмотический коэффициент также, как и коэффициент активности, показывает степень отклонения реального раствора от идеального.
Осмотическое давление идеального раствора равно:
Осмотическое давление реального раствора:
Для реального раствора, когда 
, можно записать:
Тогда можно записать:
- 
ln 
(3)
Это уравнение связывает коэффициент активности с осмотическим коэффициентом.