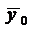Федеральное агентство по образованию
Государственное образовательное учреждение
Высшего профессионального образования
Челябинский государственный университет
Миасский филиал
Факультет управления
Кафедра «Финансы и кредит»
КОНТРОЛЬНАЯ РАБОТА
По статистике
Вариант № 2
Выполнил: студент группы МУ-201
Гаврильченко М.А.
Проверил: старший преподаватель
Савичев В.Ю.
Миасс
Задача 1. Из отчетов 24 предприятий отрасли получены следующие данные о их работе в отчетном периоде:
Таблица 1 Результаты работы предприятий
| Заводы, п/п | Стоимость основных производственных фондов, млрд.руб | Продукция в сопоставимых ценах, млрд.руб | Заводы, п/п | Стоимость основных производственных фондов, млрд.руб | Продукция в сопоставимых ценах, млрд.руб |
| 6,3 | 10,6 | 3,7 | 5,1 | ||
| 2,5 | 3,6 | 3,8 | 2,6 | ||
| 4,1 | 4,5 | 1,2 | 2,2 | ||
| 7,6 | 12,4 | 8,6 | 18,2 | ||
| 5,7 | 6,7 | 9,3 | 19,6 | ||
| 7,5 | 12,3 | 5,9 | 9,8 | ||
| 8,4 | 12,4 | 5,1 | 10,2 | ||
| 5,7 | 10,0 | 5,2 | 10,4 | ||
| 8,6 | 14,2 | 8,6 | 20,7 | ||
| 6,6 | 12,8 | 4,7 | 6,1 | ||
| 3,4 | 3,4 | 3,8 | 3,5 | ||
| 1,9 | 2,4 | 10,2 | 18,0 |
С целью изучения зависимости между стоимостью основных производственных фондов и выпуском продукции произведите группировку заводов по размеру основных фондов, образовав 5 групп заводов с равными интервалами. Проверьте число интервалов с помощью правила Стерджесса. По каждой группе подсчитайте:
1) число заводов;
2) стоимость основных производственных фондов ‑ всего и в среднем на один завод;
3) стоимость валовой продукции ‑ всего и в среднем на один завод;
4) фондоотдачу (в процентах).
Результаты представьте в виде групповой итоговой таблицы 2. Сделайте выводы.
|
|
Решение:
1) Величину интервала определяем по формуле:
,
Где: 
, 
максимальное и минимальное значение стоимости основных производственных фондов;
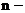число групп.
Правило Стерджесса: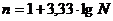 
N(число заводов) = 24
Тогда 
млрд.руб.
= 10,2; 
= 1,2
Число заводов заключено в следующих интервалах:
[1,2; 3) – 3 завода [6,6; 8.4) – 3 завода
[3; 4,8) – 6 заводов [8,4; 10,2] – 6 заводов
[4,8; 6,6) – 6 заводов
2) Фондоотдачу определяем по формуле:
Q – продукция в сопоставимых ценах, млрд.руб.;
Ф – стоимость основных производственных фондов, млрд.руб.
Итоговая таблица
| № группы | Группы заводов по размеру основных производственных фондов (интервалы), млрд.руб | Число заводов | Стоимость основных производственных фондов, млрд.руб | Продукция в сопоставимых ценах, млрд.руб | Фондоотдача, % | |||
| Всего | В среднем на один завод | Всего | В среднем на один завод | |||||
| [1,2; 3) | 5,6 | 1,8666 | 8,2 | 2,7333 | 146,428 | |||
| [3; 4,8) | 23,5 | 3,9166 | 25,2 | 4,2 | 107,234 | |||
| [4,8; 6,6) | 33,9 | 5,65 | 57,7 | 9,62 | 170,2 | |||
| [6,6; 8.4) | 21,7 | 7,2333 | 37,5 | 12,50 | 172,8 | |||
| [8,4; 10,2] | 53,7 | 8,95 | 103,1 | 17,18 | 192,0 | |||
| Итого | 138,4 | 5,7666 | 231,7 | 9,6541 | 167,41 | |||
Выводы: Заводы относительно стоимости ОПФ распределены неравномерно. Наиболее многочисленны группы заводов со средним и максимальным размером ОПФ (средние и крупные предприятия). Средняя фондоотдача по всей совокупности и в отдельности по каждой группе заводов свыше 100%, что свидетельствует об их эффективной работе.
Задача 2. Работа автокомбината характеризуется следующими данными:
|
|
Таблица 3
| Автоколонна | Общие затраты на перевозку грузов, руб. | Средний месячный грузооборот автомашины, ткм | Себестоимость одного ткм, коп |
Определите по автокомбинату в целом: а) среднюю себестоимость одного ткм; б) среднее число машин в автоколонне; в) средний месячный грузооборот автомашины.
Решение:
а) Рассчитаем среднюю себестоимость одного ткм по следующей формуле:
б) Рассчитаем среднее число машин в автоколонне по ф-ле:
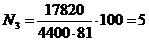
в) Рассчитаем средний месячный грузооборот машины:
Выводы: Средняя себестоимость одного ткм составляет примерно 86 коп. Количество машин в каждой из 3 автоколонн распределено неравномерно, а среднемесячный грузооборот этих машин составляет около 4895 ткм.
Задача 3. При выборочном обследовании 1% изделий партии готовой продукции получены следующие данные о содержании влаги в образцах:
Таблица 4 Содержание влаги в образцах продукции
| Содержание влаги, % | 12-14 | 14 -16 | 16-18 | 18-20 | Свыше 20 |
| Количество изделий, шт |
На основании этих данных выборочного обследования вычислите:
1) размах вариаций;
2) среднее линейное отклонение;
3) дисперсию;
4) среднее квадратичное отклонение;
5) коэффициент вариации. По коэффициенту вариации, используя правило "трех сигм", определите, однородна ли данная совокупность;
6) моду и медиану;
7) коэффициент асимметрии. Определите, какая асимметрия наблюдается в данном распределении.
Сделайте выводы по каждому пункту и по всей задаче в целом.
|
|
Решение: В расчете распределения содержания влаги в образцах продукции используем середины интервалов:
Таблица 3.1
| i |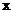 
| f | 
| 
| 
| 
| 
| 
|
| 17,21 | -4,21 | 29,47 | 124,0687 | -522,329 | ||||
| -2,21 | 55,25 | 122,1025 | -269,846 | |||||
| -0,21 | 7,35 | 1,5435 | -0,324 | |||||
| 1,79 | 35,8 | 64,082 | 114,707 | |||||
| 3,79 | 56,85 | 215,4615 | 816,599 | |||||
| 184,72 | 527,258 | 138,807 |
1. Размах вариаций
%
2. Среднее линейное отклонение
– среднее выборочное
%
%
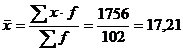3. Дисперсия
s2 
s2 
%
4. Среднее квадратичное отклонение
s 
s 
%
5. Коэффициент вариации
%
V< 33 % => данная совокупность однородна
6. Мода и медиана
- мода
Для интервальных рядов распределения с равными интервалами мода определяется по формуле:
,
где 
- начальное значение интервала, содержащего моду;
- величина модального интервала;
- частота модального интервала;
- частота интервала, предшествующего модальному;
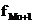- частота интервала, следующего за модальным.
%, 
%, 
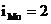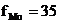шт, 
шт, 
шт.
%
Медиана интервального вариационного ряда распределения определяется по формуле:
где 
— начальное значение интервала, содержащего медиану;
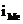— величина медианного интервала;
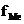— частота медианного интервала;
— сумма накопленных частот, предшествующих медианному интервалу;
%, 
%, 
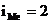шт,,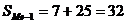 
шт, 
шт.
7. Коэффициент асимметрии
%
%
=> асимметрия правосторонняя т.к. А > 0.
Выводы: Результаты расчетов выборки, полученной при 1-ти процентном выборочном обследовании изделий, следующие:
-максимальный разброс по содержанию влаги составляет 7%;
-средняя влажность изделия – 17,3 %, со средним линейным отклонением в 1,8 % и средним квадратичным отклонением - 2,2 %;
-данную выборку изделий можно считать однородной относительно содержания в них влаги (V < 33 %);
-наиболее часто встречаемая величина содержания влаги в образце составляет 16,8%;
-изделия с влажностью до 17,1% составляют примерно половину от всех исследованных;
-по сравнению с нормальным распределением, распределение изделий по содержанию в них влаги отклонено от средней в сторону уменьшения (правосторонняя асимметрия), т.е. основная часть исследуемых изделий имеет процент влажности ниже среднего.
Задача 4. На мебельной фабрике имеются следующие данные о производстве продукции:
Таблица 5 Выпуск продукции на мебельной фабрике
| Виды продукции | Количество продукции, шт. | Себестоимость 1 шт, тыс.руб. | ||
| Базис | Отчет | Базис | Отчет | |
| Шкаф книжный | ||||
| Столы письменные |
Определите:
1) индивидуальные индексы себестоимости физического объема продукции;
2) агрегатный индекс себестоимости;
3) агрегатный индекс физического объема;
4) общий индекс затрат на продукцию;
5) абсолютную сумму экономии (перерасхода) средств в отчетном периоде от изменения себестоимости единицы продукции
Покажите взаимосвязь индексов, исчисленных в пунктах 2, 3. По результатам задачи сделайте выводы.
Решение:
Обозначим
z0, z1 – себестоимость 1 шт. соответственно в базисном и отчетном периодах;
q0, q1 – количество выпущенной продукции соответственно в базисном и отчетном периодах;
1. Индивидуальные индексы себестоимости и физического объема продукции:
; 
Для определения всех требуемых показателей составим расчетную таблицу:
Выпуск продукции на мебельной фабрике
| Виды продукции | Себестоимость 1шт, тыс.руб. | Кол-во продукции, шт. | Себестоимость произведенной продукции, млн.руб. | Индивидуальные индексы | |||||
| Базис z0 | Отчет z1 | Базис q0 | Отчет q1 | Базис | Отчет | ||||
| по ценам базиса z0q0 | по ценам базиса z0q1 | по ценам отчета z1q1 | себестои-мости iz | физического объема iq | |||||
| Шкаф книжный | 0.97 | 1,33 | |||||||
| Столы письменные | 213,594 | 0.93 | 0,45 | ||||||
| Итого: | 459,594 |
2. Агрегатный индекс себестоимости:
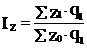
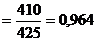или 96,4 % (- 3,6%)
3. Агрегатный индекс физического объема:
или 92,4 % (- 7,6%)
4. Общий индекс затрат на продукцию
или89,2 % (- 10,8%)
5 Абсолютная сумма экономии (перерасхода) средств в отчетном периоде от изменения себестоимости:
млн.руб.
Взаимосвязь индексов отражается следующим уравнением:
Выводы: В отчетном периоде наблюдается уменьшение: себестоимости по всем видам продукции и физического объема по письменным столам, и увеличение физического объема по книжным шкафам на 33%. Общие затраты на производство продукции в отчетном периоде сократились на 10,8% за счет понижения физического объема продукции на 7,6% и снижения себестоимости произведенной продукции на 3,6 %. Уменьшение себестоимости продукции привело к перерасходу средств в отчетном периоде на 15 млн.руб
Задача 5 Динамика средних цен и объема продаж картофеля на колхозных рынках двух городов характеризуется следующими данными:
Таблица 6 Реализация картофеля на рынках города
| Город | Средняя цена 1 кг, руб. | Продано картофеля, т. | ||
| Июль | Август | Июль | Август | |
| А | ||||
| В |
На основании этих данных вычислите:
1) индекс цен переменного состава;
2) индекс цен постоянного (фиксированного) состава;
3) индекс цен структурных сдвигов.
Покажите взаимосвязь исчисленных индексов. Сделайте выводы.
Решение:
Пусть p0, p1 – средняя цена 1 кг. картофеля в базисном и отчетном периодах;
q0, q1 – количество проданного картофеля соответственно в базисном и отчетном периодах;
Составим расчетную таблицу
| Город | Средняя цена 1 кг, руб | Продано картофеля, т | Стоимость реализованного картофеля, млн.руб | ||||
| Июль p0 | Август p1 | Июль q0 | Август q1 | Июль p0 q0 | Август p1 q1 | В августе по ценам июля p0 q1 | |
| А | |||||||
| Б | 18,12 | 30,2 | |||||
| Итого: | 43,12 | 60,2 |
1) индекс цен переменного состава
или 70,1 % (–29,9%)
2) индекс цен постоянного (фиксированного) состава
или 73,1 % (–26,9%)
3) индекс структурных сдвигов
или 95,98 % (–4,02%)
Взаимосвязь индексов:
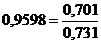
Вывод: От изменения роли отдельных городов в общем объеме продаж картофеля его средняя цена снизилась на 4,02 %, от снижения цены за 1 кг. - на 26,9 %, а всего под влиянием двух факторов - на 29,9 %.
Задача 6. Известны данные о производстве бумаги на заводе за 12 месяцев года:
Таблица 7 Выпуск бумаги на заводе по месяцам, т
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII |
Для анализа ряда динамики исчислите:
1) показатели, характеризующие динамику производства электроэнергии: абсолютный прирост, темпы роста и прироста. Результаты расчетов изложите в табличной форме (табл.8);
2) средний уровень ряда динамики, средний абсолютный прирост, средний темп роста, средний темп прироста.
Для определения основной тенденции ряда динамики произведите выравнивание ряда динамики с помощью уравнения прямой.
Сравните первоначальный и выравненный ряды с помощью столбиковой диаграммы. По результатам задачи сделайте выводы.
Таблица 8
Показатели динамики выпуска бумаги на заводе "А"
| Месяц | Выпуск бумаги, т | Абсолютный прирост, т | Темпы роста, % | Темпы прироста, % | |||
| Цепной способ | Базисный способ | Цепной способ | Базисный способ | Цепной способ | Базисный способ | ||
Решение:
1) Показатели, характеризующие динамику выпуска бумаги на заводе "А", определяем согласно следующим формулам:
Абсолютный прирост:
цепной – 
; базисный – 
Темп роста:
цепной – 
; базисный –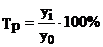 
Темп прироста:
цепной – 
; базисный – 
Где: 
текущий уровень ряда;
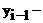уровень предшествующий 
;
начальный (базисный) уровень ряда (выпуск бумаги на заводе в I месяц).
II месяц: 
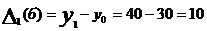т., 
т.
, 
, 
III месяц: 
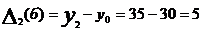т., 
т.
, 
, 
IV месяц: 
т., 
т.
, 
, 
V месяц: 
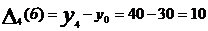т., 
т.
, 
,
VI месяц: 
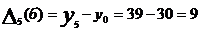т., 
т.
, 
, 
………………………………… и т.д. по всем остальным месяцам.
Таблица 8
Показатели динамики выпуска бумаги на заводе "А"
| Месяц | Выпуск бумаги, т | Абсолютный прирост, т | Темпы роста, % | Темпы прироста, % | |||
| Цепной способ | Базисный способ | Цепной способ | Базисный способ | Цепной способ | Базисный способ | ||
| I | - | - | - | - | - | - | |
| II | 133,3 | 133,3 | 33,3 | 33,3 | |||
| III | -5 | 87,5 | 116,7 | -12,5 | 16,7 | ||
| IV | 114,3 | 133,3 | 14,3 | 33,3 | |||
| V | 133,3 | 33,3 | |||||
| VI | -1 | 97,5 | 130,0 | -2,5 | 30,0 | ||
| VII | 102,6 | 133,3 | 2,6 | 33,3 | |||
| VIII | -15 | -5 | 62,5 | 83,3 | -37,5 | -16,7 | |
| IX | 168,0 | 140,0 | 68,0 | 40,0 | |||
| X | 107,1 | 150,0 | 7,1 | 50,0 | |||
| XI | -4 | 91,1 | 136,7 | -8,9 | 36,7 | ||
| XII | 107,3 | 146,7 | 7,3 | 46,7 | |||
| Итого |
2) Средний уровень ряда динамики:
т
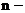число уровней ряда
Средний абсолютный прирос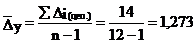т:
т
Средний темп роста:
или 103,5 %
Средний темп прироста:
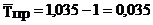или 3,5 %
Выравнивание ряда динамики методом скользящей средней по трем элементам:
| Месяц | Выпуск бумаги, т | Трехмесячный подвижной итог выпуска, т | Средняя за период, |
| т | |||
| I | - | - | |
| II | |||
| III | 38,3 | ||
| IV | 38,3 | ||
| V | 39,7 | ||
| VI | 39,7 | ||
| VII | 34,7 | ||
| VIII | 35,7 | ||
| IX | 37,3 | ||
| X | 42,7 | ||
| XI | 43,3 | ||
| XII | - | - |
Выводы: У первоначального ряда динамики выпуска бумаги на заводе "А" наблюдается скачкообразное изменение объема производства от года к году. В среднем в месяц выпускалось 38,42 т бумаги. Средний абсолютный прирост производства бумаги за месяц составил 1,273 т. В рассматриваемом периоде производство бумаги в среднем увеличивалось за месяц на 3,5 %. Выравненный ряд в сравнении с первоначальным рядом отражает плавное волнообразное изменение объема выпуска бумаги в течение года.
Задача 7. Продажа рыбы и рыбопродуктов в государственной торговле, включая общественное питание, в Российской Федерации (в сопоставимых ценах) характеризуется следующими показателями (в процентах):
Таблица 9
Реализация продуктов в сопоставимых ценах по отношению к 2000 г., %
| 2001 г. | 2002 г. | 2003 г. | 2004 г. | 2005 г. |
| 106,0 | 104,0 | 102,0 | 100,9 | 99,8 |
Вычислите:
1) ежегодные темпы роста продажи рыбы и рыбопродуктов на 2001-2005 г.г.;
2) среднегодовой темп роста реализации продуктов.
Результаты представьте в табличной форме. Сделайте выводы.
Решение:
1) Ежегодные темпы роста продажи рыбы и рыбопродуктов на 2001-2005 г.г. соответствуют цепным темпам роста за этот период, определяемым по формуле:
текущий уровень ряда;
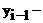уровень предшествующий .
2002 г.: 
2003 г.: 
2004 г.: 
2005г.: 
Результаты расчетов ежегодных темпов роста продажи рыбы и рыбопродуктов на 2000-2005г.г. представлены в табл. 9.1.
Таблица 9.1
Реализация продуктов в сопоставимых ценах
| Год | ||||||
| Темп роста, % | базисный | 106,0 | 104,0 | 102,0 | 100,9 | 99,8 |
| цепной | - | 98,11 | 98,08 | 98,91 | 98,90 |
2) Среднегодовой темп роста реализации:
конечный уровень ряда;
начальный (базисный) уровень ряда (уровень 2001 г.); 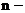число уровней ряда.
или 98,97 % (– 1,03%)
Выводы: Во всем периоде с 2000 г. по 2005 г. наблюдается снижение темпов продажи рыбы и рыбопродуктов от года к году. В среднем снижение продаж рыбы и рыбопродуктов составило 1,03 % в год.
Задача 8. Для изучения зависимости между выпуском продукции в среднем на один завод (результативный признак - у) и оснащенностью заводов основными производственными фондами (факторный признак - x) по данным задачи 1 вычислите коэффициент детерминации и эмпирическое корреляционное отношение. Поясните их значение.
Постройте линию регрессии.
Сделайте выводы по задаче.
Решение: Для определения показателей составим расчетную таблицу
Таблица 8. 1
| № завода | № группы | Число заводов,n | Продукция в сопоставимых ценах, млрд.руб y. | Стоимость ОПФ, млрд.руб x. | Продукция в среднем на один завод, млрд.руб |
|
|
| ||||||||||
| 3,6 | 2,5 | 2,73 | 9,65 | 36,6 | 143,66 | |||||||||||||
| 2,4 | 1,9 | 52,56 | ||||||||||||||||
| 2,2 | 1,2 | 55,5 | ||||||||||||||||
| 4,5 | 4,1 | 4,2 | 26,52 | 178,22 | ||||||||||||||
| 3,4 | 3,4 | 39,06 | ||||||||||||||||
| 5,1 | 3,7 | 20,7 | ||||||||||||||||
| 2,6 | 3,8 | 49,7 | ||||||||||||||||
| 6,1 | 4,7 | 12,6 | ||||||||||||||||
| 3,5 | 3,8 | 37,82 | ||||||||||||||||
| 10,6 | 6,3 | 9,62 | 0,9 | 0,005 | ||||||||||||||
| 6,7 | 5,7 | 8,7 | ||||||||||||||||
| 5,7 | 0,12 | |||||||||||||||||
| 9,8 | 5,9 | 0,02 | ||||||||||||||||
| 10,2 | 5,1 | 0,3 | ||||||||||||||||
| 10,4 | 5,2 | 0,56 | ||||||||||||||||
| 12,4 | 7,6 | 12,5 | 7,56 | 24,37 | ||||||||||||||
| 12,3 | 7,5 | 7,02 | ||||||||||||||||
| 12,8 | 6,6 | 9,92 | ||||||||||||||||
| 12,4 | 8,4 | 17,18 | 7,56 | 340,21 | ||||||||||||||
| 14,2 | 8,6 | 20,7 | ||||||||||||||||
| 18,2 | 8,6 | 73,1 | ||||||||||||||||
| 19,6 | 9,3 | |||||||||||||||||
| 20,7 | 8,6 | 122,1 | ||||||||||||||||
| 10,2 | 69,72 | |||||||||||||||||
| Итого | 231,7 | 758,34 | 686,465 |
1) Коэффициент детерминации:
- общая дисперсия
- межгрупповая дисперсия
; 
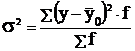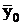- общая средняя по совокупности в целом
- среднее значение в группе
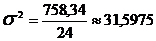млрд.руб.2
2) Эмпирическое корреляционное отношение:
Эмпирическую линии регрессии строим по величинам стоимости ОПФ и продукции в среднем на один завод (табл.2):
Выводы: По построенной эмпирической линии регрессии и величине эмпирического корреляционного отношения, составившего 0,951, можно сказать о наличии тесной прямой взаимосвязи между стоимостью основных фондов и выпуском продукции, т.е. в среднем с ростом стоимости ОПФ завода происходит увеличение выпуска его продукции.
Коэффициент детерминации равен 0,905, это значит что 90,5 % всей вариации обусловлено изучаемым фактором, т.е. стоимость выпускаемой продукции на 90,5 % обусловлена стоимостью основных фондов.
Задача 9. По данным задачи 3 определите:
1) с вероятностью 0,997 возможные пределы, в которых ожидается средний процент влажности всей готовой продукции;
2) с вероятностью 0,954 возможные пределы удельного веса, стандартной продукции при условии, что к нестандартной продукции относятся изделия с влажностью до 14% и свыше 20%.
По результатам задачи сделайте выводы.
Решение:
1) предельная ошибка выборки для средней
р=0,997 => t =3;
т.к. выборка одна процентная
По расчетным данным задачи №3: n=102, s2=5,17%
%
=17,21%
16,556 % < < 17,864 %
2) предельная ошибка выборки для доли
р=0,954 => t =2;
w 
или 
,2%
0,698< w < 0,862 или 69,8 % < р < 86,2 %
Выводы: С вероятностью 0,997 можно утверждать что средний процент влажности всей готовой продукции будет находится в пределах от 16,556 до 17,864 %. При вероятности 0,954 доля стандартной продукции, выраженная в процентах, будет составлять от 69,8 % до 86,2 %.