Программа работы
1. Последовательное соединение элементов. 2-ой закон Кирхгофа.
2. Параллельное соединение элементов. 1-ый закон Кирхгофа.
3. Смешанные соединение элементов с двумя источниками. Баланс мощностей.
Общие положения
В электрической схеме соединения элементов образуют ветви, узлы, контуры.
Ветвь образуется одним или несколькими последовательно соединенными элементами, по которым протекает один и тот же ток.
Узел - место соединения 3-х или большего числа ветвей.
Контур - любой замкнутый путь, проходящий по нескольким ветвям в электрической схеме.
Ветви, присоединенные к одной паре узлов, называются параллельными.
Законы электрических цепей
1. Первый закон Кирхгофа - закон баланса токов в узле: «Алгебраическая сумма токов, сходящихся в узле, равна 0: 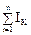 = 0.
= 0.
Электрический заряд в узле не накапливается ».
2. Второй закон Кирхгофа: «Алгебраическая сумма ЭДС источников питания в любом контуре равна алгебраической сумме падений напряжения на пассивных элементах этого контура».
 .
.
Режим постоянного тока
При постоянном токе в электрической цепи отсутствует явление самоиндукции, и напряжение на катушке индуктивности определяется только величиной падения напряжения на активном сопротивлении.
Если рассматривать конденсатор как идеальную емкость, то в цепи постоянного тока эта ветвь равносильна разомкнутой.
Постоянный ток через ёмкость не проходит.
Таким образом, в цепи постоянного тока остаются только источники ЭДС или тока - активные элементы и приёмники, резисторы - пассивные элементы.
Простыми цепями постоянного тока называются цепи с одним источником при последовательном, параллельном и смешанном соединениях приемников.
Последовательное соединение приемников

Рис. 2. Последовательное соединение приемников
E = IR1 + IR2 + ××× + IRn = I(R1 + R2 + ××× + Rn) = I Rэкв
Rэкв= SRi - при последовательном соединении сопротивления складываются (рис.2).
Параллельное соединение приемников
 |
Рис. 3. Параллельное соединение приемников
При параллельном соединении приемников напряжение на всех приемниках одинаково (рис.3).
По закону Ома, токи в каждой ветви
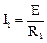 ,
,  ,...,
,..., 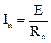 .
.
По первому закону Кирхгофа, общий ток
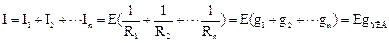
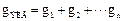
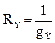
При параллельном соединении суммируются проводимости.
Смешанное соединение - комбинация последовательного и параллельного (рис.4).

Рис. 4. Этапы свертывания схемы смешанного соединения приемников
 ;
; 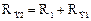 .
.
Сложной электрической цепью называют такую цепь, которая не может быть сведена только к последовательному или параллельному соединению источников и приемников электрической энергии (рис. 5).
Линейной электрической цепью называют электрическую цепь, содержащую приемники и источники электрической энергии, параметры которых (сопротивления и проводимости) остаются постоянными и не зависят от величины и направления протекающего через них тока. Зависимость тока от приложенного напряжения в таких приемниках (резисторах) изображается прямой линией, а сами резисторы называются линейными резисторами.

Рис. 5
Сложные электрические цепи имеют несколько узлов и ветвей, а также могут иметь и несколько источников питания. Ветвью электрической цепи называют участок схемы, состоящий из нескольких последовательно соединенных элементов, по которым протекает один и тот же ток. Узлом электрической цепи называют точку соединения, к которой подходит не менее трех ветвей.
Расчет сложной линейной электрической цепи заключается в определении токов во всех ветвях и сводится к решению системы линейных алгебраических уравнений, составленных по законам Кирхгофа для данной электрической цепи.
Решение системы алгебраических уравнений представляет собой достаточно трудоемкую работу, объем которой возрастает с увеличением числа неизвестных при увеличении сложности электрической цепи.
В целях сокращения числа уравнений, решение которых даст искомые величины и определит режим электрической цепи, разработаны различные методы расчета линейных электрических цепей: например, метод контурных токов, где уравнения составляются только по второму закону Кирхгофа, или метод узловых потенциалов, когда уравнения составляются только по первому закону Кирхгофа.
В данной лабораторной работе экспериментально исследуется метод расчета электрических цепей с помощью составления и решения уравнений по первому и второму законам Кирхгофа.
Первый закон Кирхгофа формулируется следующим образом: сумма притекающих к узлу токов равна сумме вытекающих из узла токов или алгебраическая сумма токов в узле равна нулю, т. е.
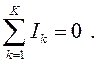
Например, для узла b (см. рис. 5):  или
или
 .
.
Второй закон Кирхгофа гласит: в любом замкнутом контуре электрической цепи алгебраическая сумма падений напряжения на всех сопротивлениях этого контура равна алгебраической сумме ЭДС, действующих в этом контуре, т. е.
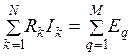 .
.
Например, для контура abda:
R 1· I 1+ R 3· I 3= E 1 .
Для контура cbdc:
R 2· I 2+ R 3· I 3= E 2 .
Запишем уравнения в канонической форме. Для этого расположим неизвестные в уравнениях в порядке их нумерации и заменим отсутствующие члены членами с нулевыми коэффициентами:
I 1 + I 2 – I 3 = 0
R 1· I 1+ 0· I 2+ R 3· I 3 = E 1
0· I 1+ R 2· I 2+ R 3· I 3 = E 2,
или в матричной форме:

После подстановки численных значений ЭДС и сопротивлений полученная система уравнений решается известными из математик и методами, например методом Крамера или методом Гаусса. Можно решить эту систему и в интегрированном пакете MATHCAD.
В любой электрической цепи выполняется закон сохранения энергии, т. е. мощность, развиваемая источниками электрической энергии равна сумме мощностей, потребляемых приемниками электрической энергии. Этот баланс мощностей записывается следующим образом:
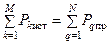
или  .
.