Задание 1
Представить графически область начальных приближений в квадрате  , обеспечивающих сходимость к нулевому решению, для метода а) градиентного спуска с длиной шага
, обеспечивающих сходимость к нулевому решению, для метода а) градиентного спуска с длиной шага  ; б) Ньютона применительно к функционалу:
; б) Ньютона применительно к функционалу:
I) 

II) 

Задание 2
Найти минимум функции


методом градиентного спуска с начальными приближениями  и
и  . Экспериментально определить постоянный шаг градиентного спуска
. Экспериментально определить постоянный шаг градиентного спуска  , при котором достигается наивысшая скорость сходимости метода. Представить графически зависимость скорости сходимости
, при котором достигается наивысшая скорость сходимости метода. Представить графически зависимость скорости сходимости  (число итераций) с точностью до
(число итераций) с точностью до  от шага
от шага  .
.
Задание 3
Методом наискорейшего градиентного спуска найти минимум целевой функции


с точностью до  при начальном приближении
при начальном приближении  , и оценить скорость сходимости
, и оценить скорость сходимости  (число итераций) метода в зависимости от параметра
(число итераций) метода в зависимости от параметра  .
.
Задание 4
Методом наискорейшего градиентного спуска найти минимум функции


с точностью до  при начальных приближениях
при начальных приближениях  и
и  . Оценить скорость сходимости
. Оценить скорость сходимости  (число итераций). Графически представить траекторию приближений на плоскости
(число итераций). Графически представить траекторию приближений на плоскости  и величину выбираемого переменного шага
и величину выбираемого переменного шага  метода в зависимости от номера итерации.
метода в зависимости от номера итерации.
Задание 5
Численно найти минимум функции
I) 

II)  (функция Розенброка)
(функция Розенброка)

методами а) наискорейшего градиентного спуска; б) Ньютона; в) покоординатного спуска с точностью до  при начальных приближениях I)
при начальных приближениях I)  и
и  ; II)
; II) 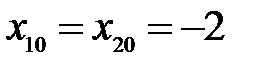 и
и  . Оценить скорость сходимости
. Оценить скорость сходимости  (число итераций), а также графически представить траекторию приближений на плоскости
(число итераций), а также графически представить траекторию приближений на плоскости  . Для I) минимум:
. Для I) минимум:  ; для II) минимум:
; для II) минимум:  .
.
Задание 6
В квадрате  методами а) наискорейшего градиентного спуска; б) Ньютона; в) покоординатного спуска с точностью до
методами а) наискорейшего градиентного спуска; б) Ньютона; в) покоординатного спуска с точностью до  численно найти все минимумы функции Химмельблау
численно найти все минимумы функции Химмельблау


Графически представить траекторию приближений от начального  к минимуму
к минимуму 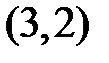 .
.
Рекомендации: шаг метода наискорейшего градиентного спуска выбирать по формуле

Задание 7
Оценить скорость сходимости  (число итераций) метода а) наискорейшего градиентного и б) покоординатного спуска при минимизации функции Бута
(число итераций) метода а) наискорейшего градиентного и б) покоординатного спуска при минимизации функции Бута


с точностью до  в зависимости от начальных приближений (пунктирная окружность), равноудаленных от минимума
в зависимости от начальных приближений (пунктирная окружность), равноудаленных от минимума 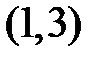 :
:

Представить зависимость  графически на отрезке
графически на отрезке  .
.
Задание 8
Оценить скорость сходимости  в зависимости от начальных приближений в квадрате
в зависимости от начальных приближений в квадрате  для метода наискорейшего градиентного спуска применительно к функционалу
для метода наискорейшего градиентного спуска применительно к функционалу


Зависимость  представить графически.
представить графически.
Рекомендации: шаг метода выбирать по формуле

ТЕМА 5. ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
Задание 1
Вычислить определенный интеграл
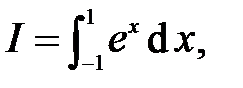
используя квадратурные формулы а) Ньютона–Котеса с количеством узлов  ; б) Гаусса с количеством узлов
; б) Гаусса с количеством узлов 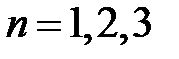 ; в) составные Симпсона с разбиениями
; в) составные Симпсона с разбиениями  . Оценить ошибку численного решения, сравнивая его с точным значением интеграла.
. Оценить ошибку численного решения, сравнивая его с точным значением интеграла.
Задание 2
Используя формулу Симпсона, вычислить интеграл

где  . Оценить ошибку численного решения, сравнивая его с точным значением интеграла.
. Оценить ошибку численного решения, сравнивая его с точным значением интеграла.
Задание 3
Вычислить определенный интеграл

используя составные квадратурные формулы трапеции. Исследовать зависимость ошибки численного решения от числа разбиений 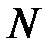 составной формулы. Рассмотреть
составной формулы. Рассмотреть  , где
, где 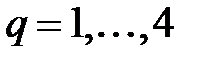 .
.
Задание 4
Стохастическим методом (Монте-Карло) вычислить определенный интеграл

и оценить методическую ошибку в зависимости от количества испытаний  . Рассмотреть
. Рассмотреть 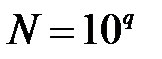 , где
, где  .
.
Задание 5
Статистическим методом (Монте-Карло) вычислить определенные интегралы

и оценить методическую ошибку в зависимости от количества испытаний  . Рассмотреть
. Рассмотреть 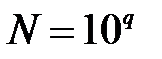 , где
, где  .
.
Задание 6
Используя составную квадратурную формулу Гаусса, точную для полиномов третьей степени, вычислить определенный интеграл

и оценить точность численного решения в зависимости от числа разбиений N. Рассмотреть  , где
, где  .
.
Задание 7
Вычислить определенный интеграл

используя составную квадратурную формулу Симпсона. Исследовать зависимость ошибки численного решения от длины подотрезка интегрирования 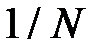 . Рассмотреть
. Рассмотреть  , где
, где 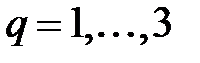 .
.