Пример 2. Решить матричное уравнение
.
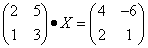Пример 3. Решить матричное уравнение
.
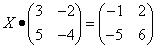Решение. Данное уравнение имеет вид X ⋅ A = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде 
, то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A.
Сначала найдём определитель матрицы A:
.
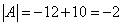Найдём алгебраические дополнения матрицы A:
.
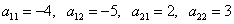Составим матрицу алгебраических дополнений:
.
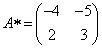Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
.
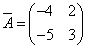Находим матрицу, обратную матрице A:
.
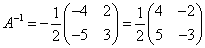Находим неизвестную матрицу:
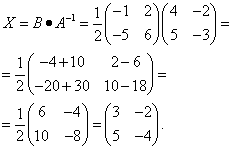
До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь матриц третьего порядка.
Пример 4. Решить матричное уравнение
.
Решение. Это уравнение первого вида: A ⋅ X = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде 
, то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A.
Сначала найдём определитель матрицы A:
.
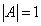Найдём алгебраические дополнения матрицы A:
Составим матрицу алгебраических дополнений:
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
.
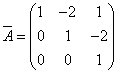Находим матрицу, обратную матрице A, и делаем это легко, так как определитель матрицы A равен единице:
.
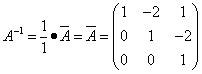Находим неизвестную матрицу:
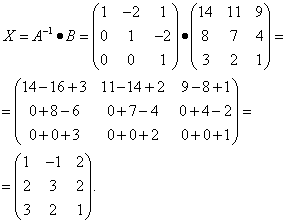
Пример 5. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид X ⋅ A = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A.
Сначала найдём определитель матрицы A:
.
Найдём алгебраические дополнения матрицы A:
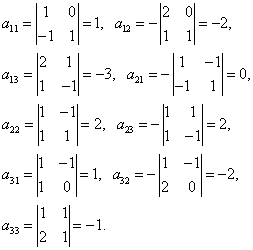
Составим матрицу алгебраических дополнений:
.
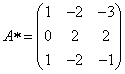Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
.
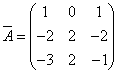Находим матрицу, обратную матрице A:
.
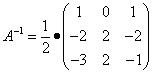Находим неизвестную матрицу:
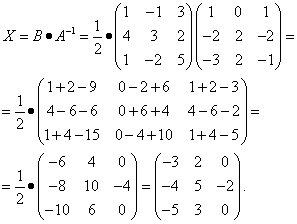
Пример 6. Решить матричное уравнение
.
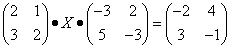Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C, то есть неизвестная матрица X находится в середине произведения трёх матриц. Поэтому решение следует искать в виде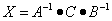 
. Найдём матрицу, обратную матрице A.
Сначала найдём определитель матрицы A:
.
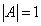Найдём алгебраические дополнения матрицы A:
.
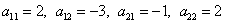Составим матрицу алгебраических дополнений:
.
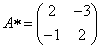Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
.
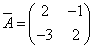Находим матрицу, обратную матрице A:
.
Найдём матрицу, обратную матрице B.
Сначала найдём определитель матрицы B:
.
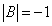Найдём алгебраические дополнения матрицы B:
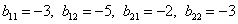
Составим матрицу алгебраических дополнений матрицы B:
.
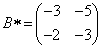Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей B:
.
Находим матрицу, обратную матрице B:
.
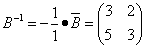Находим неизвестную матрицу:
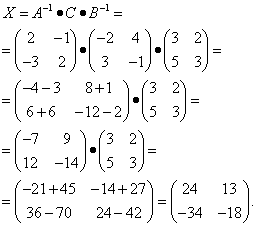
Задания для самостоятельной работы
| № варианта | Задание: решить матричное уравнение | Ф.И. выполняющего |
1) 
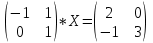2) 
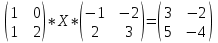
| Гордой Е. | |
1) 
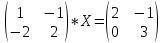2)
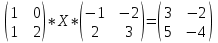
| Погорелов М. | |
1)
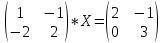2) 
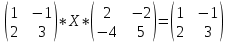
| Сургутская Л. | |
1) 
2)
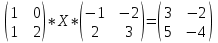
| Кириченко И. | |
| 1)
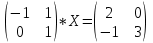2)
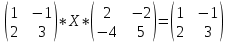
| Рябинова Е. | |
1) 
2)
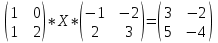
| Чернышева В. | |
| 1)
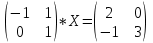2)
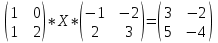
| Сердюкова А. | |
1) 
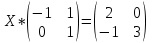2)
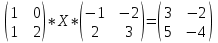
| Абушкевич Н. |