Выполнила ученица 11 А класса Ковалева Дарья
Учитель Багирян Нонна Александровна
Содержание:
Центральная симметрия
· определение и основные свойства
· построение
· фигуры, обладающие центральной симметрией
· применение в жизни
· задачи
Зеркальная симметрия
· определение и построение
· основные свойства
· фигуры, обладающие зеркальной симметрией
· зеркальная симметрия в реальной жизни
· задачи.
ЦЕНТРАЛЬНАЯ СИММЕТРИЯ.
Центральной симметрией называют преобразование пространства относительно точки A, переводящее точку X в такую точку X′, что A — середина отрезка XX′. Фигура называется симметричной относительно точки A, если для каждой точки фигуры симметричная ей точка относительно точки A также принадлежит этой фигуре. Точка A называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.
Другие названия этого преобразования — симметрия с центром A. Центральная симметрия в планиметрии является частным случаем поворота, точнее, является поворотом на 180 градусов.
Свойства:
· Центральная симметрия является движением;
· Любая прямая при центральной симметрии преобразуется в прямую. Причем, прямая, проходящая через центр, преобразуется в себя. Прямая, не проходящая через центр, преобразуется в параллельную ей прямую. (доказано в задаче 2)
· Центральная симметрия сохраняет расстояния между точками.
· Центральная симметрия переводит отрезки в отрезки, лучи в лучи.
Докажем, что центральная симметрия является движением.
Обозначим буквой O центр симметрии и введем в прямоугольную систему координат Oxyz с началом в точке О. Установим связь между координатами двух точек M (x; y; z) и M ₁ (x₁; y₁; z₁), симметричных относительно точки О.
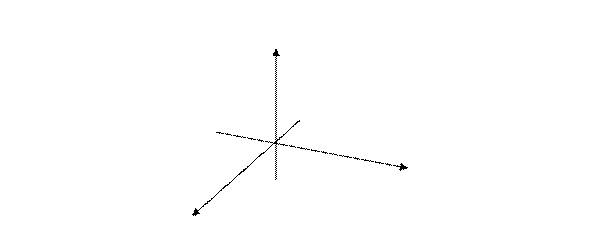
Если точка М не совпадает с центром О, то О – середина отрезка ММ₁. По формулам координат середины отрезка получаем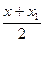 
= 0, 
= 0,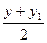 
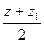=0, откуда x₁ = -x, y₁= -y, z₁ = -z.
Рассмотрим теперь две точки А (x₁; y₁; z₁) и В (x₂; y₂; z₂) и докажем, что расстояние между симметричными им точкам А₁ и В₁ равно АВ. Точки А₁ и В₁ имеют координаты А₁ (- x₁; -y₁; -z₁) и В₁ (-x₂; -y₂; -z₂). По формуле расстояния между двумя точками находим: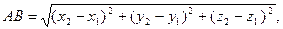 
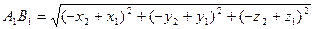. Из этих соотношений ясно, что АВ=А₁В₁, что и требовалось доказать.
Построение.
Построим точку А₀ симметричную точке А относительно точки О.
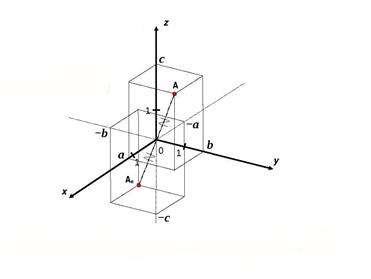
Пусть А (a; b; c). Тогда координаты A₀ (-a; -b; -c).
Фигуры, обладающие центральной симметрией.
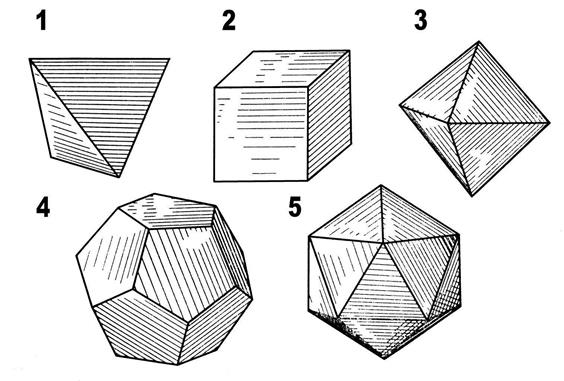
1. – тетраэдр 2. – куб 3. – октаэдр 4. – додекаэдр 5. – икосаэдр
Применение центральной симметрии в жизни.
В архитектуре центральная симметрия используется реже осевой. Она присуща античным круглым храмам, используется в колоннах.
Колизей Пирамиды в Египте
Башни церквей, замков, колонны проектировались с учетом центральной симметрии. Такие сооружения предавали зданиям массивности. Башни одинаково роскошно выглядели с любой плоскости города.
Центральная симметрия в природе. Она присутствует в снежинках, листьях деревьев и трав, насекомых, цветах, животных.
Центральная симметрия прослеживается в
национальных
костюмах казанских татар
Задачи
№ 1. Найдите координаты точек, в которые переходят точки А (0; 1; 2), В (3; -1; 4), С (1; 0; -2) при центральной симметрии относительно начала координат.
Решение:
При центральной симметрии относительно начала координат знаки координат искомых точек меняются на противоположные.
А (0; 1; 2) → А₁ (0; -1; -2)
В (3; -1; 4) → В₁ (-3; 1; -4)
С (1; 0; -2) → С₁ (-1; 0; 2)
№ 2. Докажите, что при центральной симметрии: а) прямая, не проходящая через центр симметрии, отображается на параллельную ей прямую; б) прямая, проходящая через центр симметрии, отображается на себя.
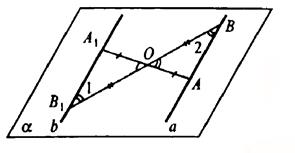а)
Решение:
Через центр симметрии и данную прямую можно провести единственную плоскость. Пусть О — центр симметрии, а — данная прямая, α — плоскость, проведенная через О и а. Пусть А ∈ а, построим отрезок ОА.
Продолжим ОА за точку О на расстояние ОА1=АО. Получим точку А1, симметричную А.
Пусть В ∈ а, построим отрезок ОВ. Продолжим ОВ за точку О на расстояние ОВ1=ОВ. Получим точку B1, симметричную точке В.
Через А1 и В1 проведем прямую b. Рассмотрим ΔAОВ и ΔА1ОВ1⋅AО=А1О, ВО=ОВ1, ΔАОВ=ΔА1ОВ1 как вертикальные, следовательно, ΔAОВ=ΔА1ОВ1.
Тогда, ∠1=∠2 и а || b.
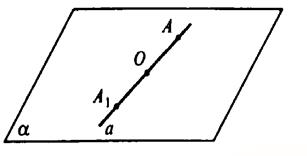
б)
Решение:
Пусть А ∈ а. Симметричная ей точка А1 тоже принадлежит прямой а; АО=ОА1.
Точка А произвольна, следовательно, любая точка прямой, а также симметричная точка относительно центра О лежат на прямой а, следовательно, прямая а переходит сама в себя при условии, что проходит через центр симметрии.
ЗЕРКАЛЬНАЯ СИММЕТРИЯ.
Зеркальной симметрией (симметрией относительно плоскости α) называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М₁ относительно плоскости α.
Докажем, что зеркальная симметрия является движением.
Для этого введем прямоугольную систему координат Оxyz так, чтобы плоскость Oxy совпала с плоскостью симметрии, и установим связь между координатами точек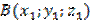 
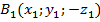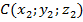и 
, 
и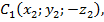 
симметричных относительно плоскости Oxy
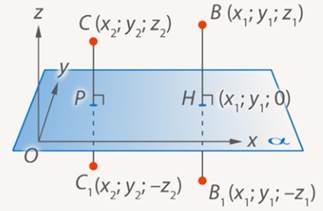
Найдем длину отрезков BC и B₁C₁ по формуле расстояния между точками:
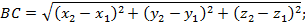
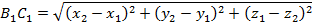
Отсюда BC = B₁C₁, значит, зеркальная симметрия является движением.
Отсюда следует, что зеркальная симметрия обладает следующими свойствами:
· переводит прямые в прямые
· полупрямые – в полупрямые
· отрезки – в отрезки
· плоскости – в плоскости
· сохраняет углы между прямыми.
Фигуры, обладающие зеркальной симметрией
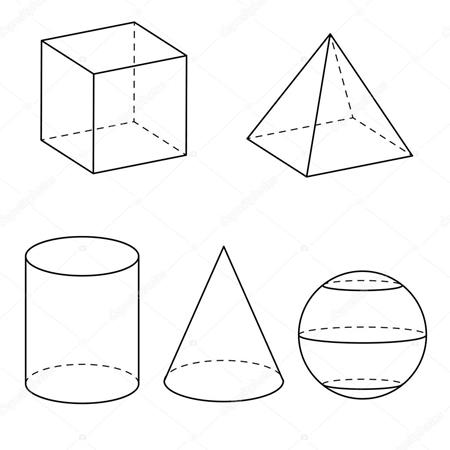
(слева на право) – куб, пирамида, цилиндр, конус, сфера
Зеркальная симметрия в жизни
Наиболее распространена в архитектуре зеркальная симметрия.
Эйфелева башня Тадж Махал
Зеркальная симметрия в природе может быть представлена отражением изображения в воде.
Животные, растения, и человек тоже могут послужить примерами зеркальной симметрии. Однако назвать их идеальными примерами сложно, ведь даже лицо человека, которое на первый взгляд может показаться симметричным, таковым не является.
Задачи:
№ 1. Найдите координаты точек, в которые переходят точки А (0; 1; 2), В (3; -1; 4), С (1; 0; -2) при зеркальной симметрии относительно координатных плоскостей.
Решение:
Если плоскость симметрии - плоскость Оxy, то меняем значение координаты z на противоположную (т.к. ось Оz перпендикулярна плоскости Оxy, О – точка их пересечения)
А (0; 1; 2) → А₁ (0; 1; -2)
В (3; -1; 4) → B₁ (3; -1; -4)
С (1; 0; -2) → C₁ (1; 0; 2)
Аналогично решение с другими плоскостями.
Если плоскость симметрии - плоскость Оyz, то меняем значение координаты x.
А (0; 1; 2) → А₁ (0; 1; 2)
В (3; -1; 4) → B₁ (-3; -1; 4)
С (1; 0; -2) → C₁ (-1; 0; -2)
Если плоскость симметрии - плоскость Оxz, то меняем значение координаты y.
А (0; 1; 2) → А₁ (0; -1; 2)
В (3; -1; 4) → B₁ (3; 1; 4)
С (1; 0; -2) → C₁ (1; 0; -2)
№ 2. При зеркальной симметрии относительно плоскости α плоскость β отображается на плоскость β₁. Докажите, что если: а) β || α, то β₁ || α; б) β ┴ α, то β₁ совпадает с β.
Решение:
а) Выберем три точки в плоскости А, В, С, не лежащие на одной прямой. Проведем АА2⊥α, ВВ2 ⊥α, СС2 ⊥α. Продолжим эти отрезки за точки А1, B1, C1 так, что А2А1=АА2, B2B1=BB2, C2C1=CC2.
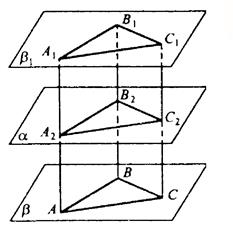
AA1B1B — прямоугольник, т.к. АА1=ВВ1 и АА1|| ВВ1. Таким образом, A1В1||АВ. ВВ1С1С — прямоугольник, т.к. BB1=CC1 и BB1|| BС. тогда, В1С1 || ВС.
Плоскость β1 проходит через точки А1, В1 и C1, она — единственная.
Если две пересекающиеся прямые (ВА и ВС) одной плоскости (β) параллельны двум прямым (B1A1 и В1С1) другой плоскости (β1), то эти плоскости параллельны: β1 || β.
б)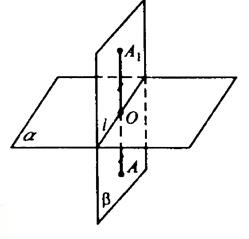 
Пусть α⊥β. Возьмем произвольную точку А ∈ β и построим АО перпендикулярно плоскости α. Продолжим отрезок за точку О на расстояние ОА1=АО.
Две плоскости взаимно перпендикулярны и к одной из них проведен перпендикуляр, имеющий общую точку с другой плоскостью, тогда этот перпендикуляр весь лежит в этой плоскости, т.е.
АО⊂β, следовательно, и АА1 ⊂β.
Таким образом, каждая точка плоскости β отображается в точку, ей симметричную, которая тоже принадлежит плоскости β. тогда, плоскость β отображается сама на себя, или β1 совпадает с β.