Предположим, что экономист-теоретик сформулировал следующие положения:
- потребление есть возрастающая функция от имеющегося в наличии дохода, но возрастающая, видимо, медленнее, чем рост дохода;
- объем инвестиций есть возрастающая функция национального дохода и убывающая функция характеристики государственного регулирования (например, нормы процента);
- национальный доход есть сумма потребительских, инвестиционных и государственных закупок товаров и услуг.
Наша первая задача - перевести эти положения на математический язык. И тут исследователь сталкивается с множеством проблем. Какие соотношения выбрать между переменными (линейные или нелинейные)? Если остановиться на нелинейных, то какими они должны быть - логарифмическими, полиномиальными или какими-либо еще? Даже определив форму конкретного соотношения, мы оставляем нерешенной проблему выбора для различных уравнений запаздываний во времени. Бyдyт ли, например, инвестиции текущего периода реагировать только на национальный доход, произведенный в последнем периоде, или же на них скажется динамика нескольких предыдущих периодов? Обычный выход из этих трудностей состоит в выборе при первоначальном анализе наиболее простой из возможных форм этих соотношений. Тогда появляется возможность записать на основе указанных выше положений следующую линейную относительно анализируемых переменных и аддитивную относительно случайных составляющих модель:
1) 
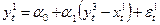функция потребления;
2) 
функция инвестиций;
3) 
функция НД,
где априорные ограничения выражены неравенствами 
, 
, 
.
Эти три соотношения вместе с ограничениями образуют модель. В ней 
обозначает подоходный налог, 
- норму процента как инструмент государственного регулирования, 
- государственные закупки товаров и услуг, измеренные в момент времени t.
Присутствие в уравнениях (1) и (2) "остаточных" случайных составляющих 
и 
обусловлено необходимостью учесть влияние соответственно на 
и 
ряда неучтенных факторов. Действительно, нереалистично ожидать, что величина потребления будет однозначно определяться уровнями национального дохода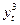 
и подоходного налога ; аналогично величина инвестиций зависит, очевидно, не только от достигнутого в предыдущий год уровня национального дохода 
и от величины нормы процента , но и от ряда неучтенных в уравнении (2) факторов.
Полученная модель содержит два уравнения, объясняющие поведение потребителей и инвесторов, и одно тождество. С.А. Айвазян и В.С Мхитарян сформулировали ее для дискретных периодов времени и выбрали запаздывание (лаг) в один период для отражения воздействия национального дохода на инвестиции.
Здесь приведен этот пример, чтобы объяснить общие черты одного из важнейших этапов эконометрического моделирования, в процессе которого исследователь математически формализует отдельные положения экономической теории и объединяет их в систему.
В этом примере потребление , инвестиции и национальный доход 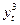в текущий момент времени t являются эндогенными переменными; подоходный налог , норма процента как инструмент государственного регулирования и государственные закупки товаров и услуг - экзогенные переменные, которые вместе с национальным доходом в предыдущий момент времени образуют множество предопределенных переменных.
Таким образом, можно сказать, что эконометрическая модель служит для объяснения поведения эндогенных переменных в зависимости от значений экзогенных и лаговых эндогенных переменных.
